初中数学浙教版（2024）八年级上册1.1 认识三角形教课ppt课件

这是一份初中数学浙教版（2024）八年级上册1.1 认识三角形教课ppt课件，共33页。

知识点1　三角形的角平分线
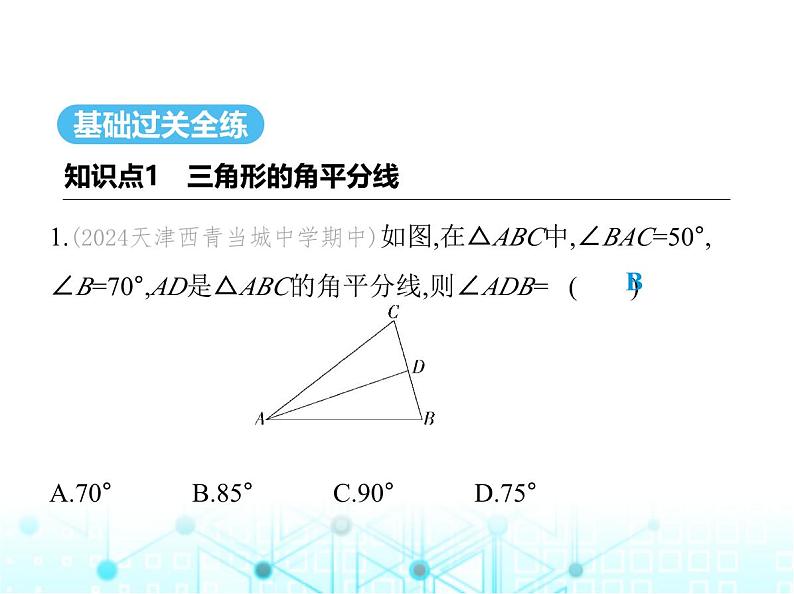
1.(2024天津西青当城中学期中)如图,在△ABC中,∠BAC=50°,∠B=70°,AD是△ABC的角平分线,则∠ADB= (　　)A.70°　　    B.85°　　    C.90°　　    D.75°
解析    ∵∠BAC=50°,AD是△ABC的角平分线,∴∠BAD= ∠BAC=25°,∴∠ADB=180°-∠B-∠BAD=180°-70°-25°=85°. 故选B.
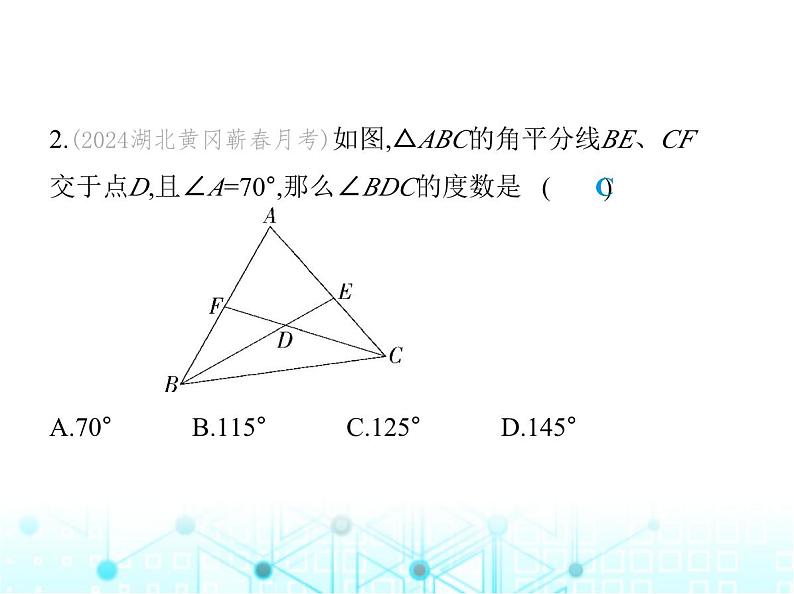
2.(2024湖北黄冈蕲春月考)如图,△ABC的角平分线BE、CF 交于点D,且∠A=70°,那么∠BDC的度数是 (　　) A.70°　　    B.115°　　    C.125°　　    D.145°
解析    ∵∠A=70°,∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,∵BE、CF是△ABC的角平分线,∴∠EBC+∠FCB=  (∠ABC+∠ACB)=55°,∴∠BDC=180°-55°=125°.故选C.
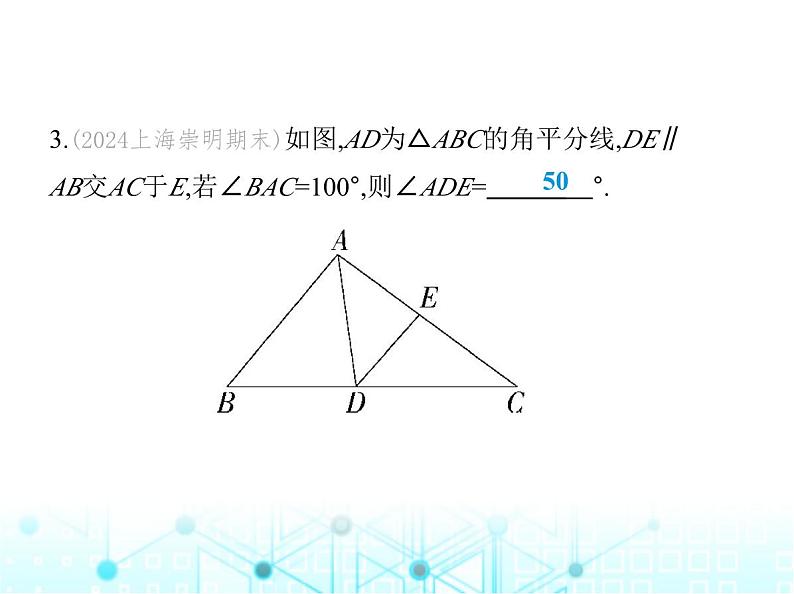
3.(2024上海崇明期末)如图,AD为△ABC的角平分线,DE∥ AB交AC于E,若∠BAC=100°,则∠ADE=　　　    °.
解析　∵AD为△ABC的角平分线,∠BAC=100°,∴∠BAD=∠CAD= ×100°=50°,∵DE∥AB,∴∠ADE=∠BAD=50°.故答案为50.
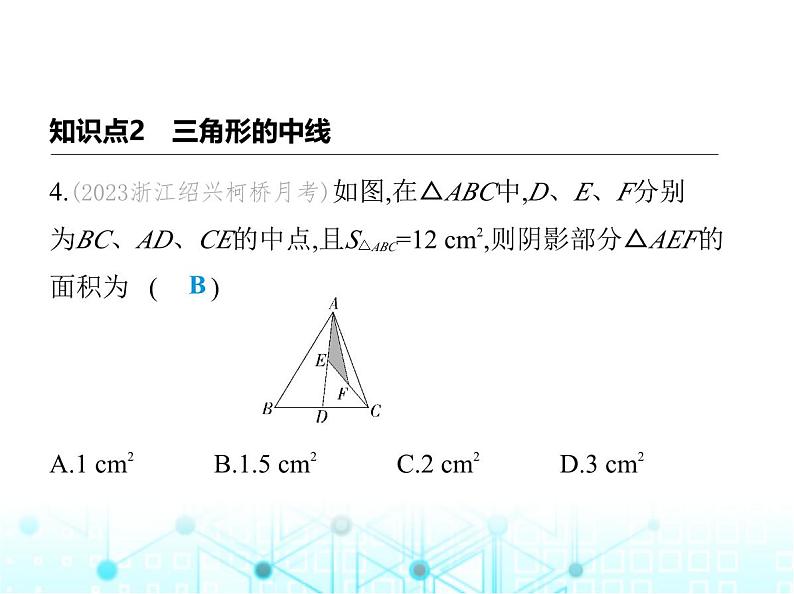
4.(2023浙江绍兴柯桥月考)如图,在△ABC中,D、E、F分别 为BC、AD、CE的中点,且S△ABC=12 cm2,则阴影部分△AEF的 面积为 (　　) A.1 cm2　　    B.1.5 cm2　　    C.2 cm2　　    D.3 cm2
知识点2　三角形的中线
解析    ∵S△ABC=12 cm2,D为BC的中点,∴S△ADC= S△ABC= ×12=6(cm2),∵E为AD的中点,∴S△AEC= S△ADC= ×6=3(cm2),∵F为EC的中点,∴S△AEF= S△AEC= ×3=1.5(cm2).故选B.
5.(整体思想)(2024广东东莞期中)如图,已知AE是△ABC的边 BC上的中线,若AC=6,△AEC的周长比△AEB的周长多1,则 AB=　　　    .
解析　∵AE是△ABC的边BC上的中线,∴CE=BE,∵△ACE的周长比△AEB的周长多1,∴(AC+AE+CE)-(AB+BE+AE)=1,即AC-AB=1,∵AC=6,∴AB=5,故答案为5.
6.(2024浙江绍兴期中)下图中,正确画出△ABC中AC边上的 高的是 (　　)A.②　　    B.③　　    C.④　　    D.①
知识点4　三角形的高线
解析    根据三角形高线的定义,AC边上的高是过点B向AC作 垂线,垂足为E,纵观各图形,①②③都不符合高线的定义,④符 合高线的定义.故选C.
7.(2023浙江杭州拱墅公益中学三模)若AM,AN分别是△ABC 的高线和中线,AG是△ABC的角平分线,则 (　　)A.AM解析    ∵线段AM,AN分别是△ABC的边BC上的高线和中线, AG是△ABC的角平分线,∴根据垂线段最短可知AM≤AN,AM≤AG.故选D.
8.(2022河南周口沈丘期末,10,★★☆)如图,在△ABC中,∠1= ∠2,G为AD的中点,延长BG交AC于E,F为AB上一点,CF⊥AD 于H,下面判断正确的有 (　　)
①AD是△ABE的角平分线;②BE是△ABD边AD上的中线; ③CH是△ACD边AD上的高;④AH是△ACF的角平分线和高.A.1个　　    B.2个　　    C.3个　　    D.4个
解析    根据三角形角平分线的概念,知AG是△ABE的角平分 线,故①错误;根据三角形中线的概念,知BG是△ABD边AD上 的中线,故②错误;根据三角形高的概念,知CH为△ACD边AD 上的高,故③正确;根据三角形角平分线和高的概念,知AH是 △ACF的角平分线和高,故④正确.故选B.
9.(面积法)(2023浙江金华东阳三模,6,★★☆)在△ABC中,BC 与BC边上的中线长分别为8 cm,4 cm,则△ABC的面积不可能 为 (　　)A.4 cm2　　     B.8 cm2C.16 cm2　　    D.32 cm2
解析    如图,AN为BC边上的中线,过A作AM⊥BC于M,由垂线段最短知AM≤AN=4 cm,∴S△ABC= BC·AM= ×8×AM=4AM≤16 cm2.∴△ABC的面积不可能为32 cm2.故选D. 
10.(2024浙江绍兴月考,8,★★☆)如图,在△ABC中,已知D,E, F分别是边AC,BD,CE的中点,且阴影部分图形的面积为7,则 △ABC的面积为 (　　) A.14　　    B.21　　    C.28　　    D.32
解析    ∵点E是BD的中点,∴S△ABE= S△ABD,S△BCE= S△BDC,∴S△ABE+S△BCE= S△ABC,∴S△ACE= S△ABC,∵点F是CE的中点,∴S△AEF= S△ACE,∴S△ABC=4S△AEF=4×7=28,故选C.
11.(新考法)(2023浙江金丽衢十二校模拟,9,★★★)在学完八 上《三角形的初步认识》一章后,某班组织了一次数学活动 课,老师让同学们自己谈谈对三角形相关知识的理解.小峰 说:“存在这样的三角形,它的三条高之比可以为1∶1∶2, 1∶2∶3,2∶3∶4,3∶4∶5.”老师说有一个三角形是不存在 的,你认为不存在的三角形的三条高之比是 (　　)A.1∶1∶2　　    B.1∶2∶3C.2∶3∶4　　    D.3∶4∶5
解析    假设存在这样的三角形,对于A选项,根据等积法,得到 此三角形三边比为2∶2∶1,∴存在这样的三角形,故不符合 题意;对于B选项,同理可得,三边比为6∶3∶2,这与三角形三 边关系相矛盾,所以这样的三角形不存在,故符合题意;对于C 选项,同理可得,三边比为6∶4∶3,存在这样的三角形,故不符 合题意;对于D选项,同理可得,三边比为20∶15∶12,存在这 样的三角形,故不符合题意.故选B.
12.(新独家原创)学习了三角形的中线、高线、角平分线后, 小华给同桌小文出了如下题目:你手里只有一张透明的三角 形纸片和一把无刻度的直尺及铅笔,你不能直接作三角形的 　　　    .(填“中线”“高线”或“角平分线”)
解析　如图,将△ABC折叠,使AC边落在AB边所在的直线上, 展开得到折痕,折痕就是∠BAC的平分线.将△ABC折叠,使点 B与点C重合,线段BC与折痕的交点(设为点D)即为线段BC的 中点,连结AD,AD就是BC边上的中线.利用提供的材料无法 作出高线.
13.(2024浙江台州仙居期末,20,★★☆)如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数. 
解析　∵∠BAC=80°,∠B=60°,∴∠ACB=180°-80°-60°=40°.∵CF平分∠ACB,∴∠ACF= ∠ACB= ×40°=20°.∵AD⊥BC,∴∠ADC=90°,∴∠CAD=180°-90°-40°=50°,∴∠AEC=180°-50°-20°=110°.
14.(2022湖北黄冈浠水月考,17,★★☆)在△ABC中,AC=2BC, BC边上的中线AD把△ABC的周长分成70和50两部分,求AC 和AB的长.
解析　∵AD是BC边上的中线,∴BD=CD,设BD=CD=x,则BC=2x,∴AC=2BC=4x,分为两种情况:①当AC+CD=70,AB+BD=50时,4x+x=70,解得x=14,∴BC=2x=2×14=28,AC=4x=4×14=56,BD=CD=14,∴AB=50- BD=50-14=36,∵BC+AB=28+36=64,AC=56,64>56,∴能组成三角形,此时AC =56,AB=36;
②当AC+CD=50,AB+BD=70时,4x+x=50,解得x=10,∴BC=2x=2×10=20,AC=4x=4×10=40,BD=CD=10,∴AB=70- BD=70-10=60,∵BC+AC=20+40=60,AB=60,60=60,∴不能组成三角形,舍去.综上所述,AC=56,AB=36.
15.(推理能力)如图,在△ABC中,AD⊥BC于D,AE平分∠BAC 交BC于E,∠B=70°,∠C=30°.(1)求∠BAE的度数.(2)求∠DAE的度数.(3)探究:如果将条件∠B=70°,∠C=30°改成∠B-∠C=40°,还 能得出∠DAE的度数吗?若能,请你写出求解过程;若不能,请 说明理由.
解析　(1)∵∠B+∠C+∠BAC=180°,∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°,∵AE平分∠BAC,∴∠BAE= ∠BAC=40°.(2)∵AD⊥BC,∴∠ADB=90°,∴∠BAD=180°-90°-∠B=90°-70°=20°,∴∠DAE=∠BAE-∠BAD=40°-20°=20°.(3)能.∵∠B+∠C+∠BAC=180°,∴∠BAC=180°-∠B-∠C,