

还剩12页未读,
继续阅读
成套系列资料,整套一键下载
数学高教版(2021)4.6.2 正弦函数的性质获奖ppt课件
展开
这是一份数学高教版(2021)4.6.2 正弦函数的性质获奖ppt课件,共20页。PPT课件主要包含了-3π,1定义域,关键点,情境导入,2值域,探索新知,3周期性,4奇偶性,5单调性,典例剖析等内容,欢迎下载使用。
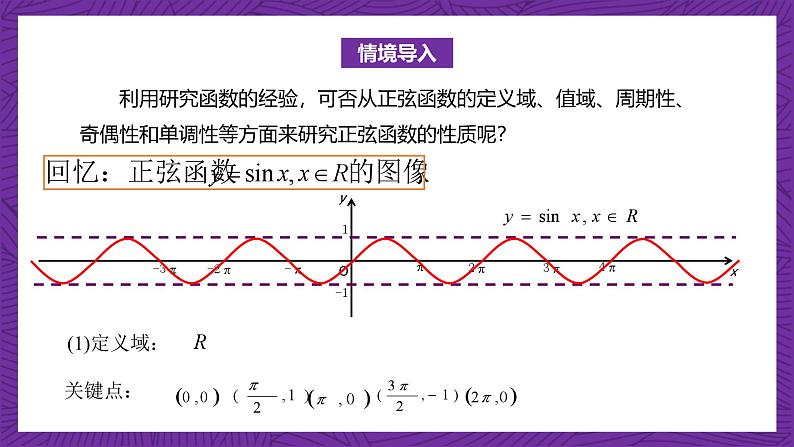
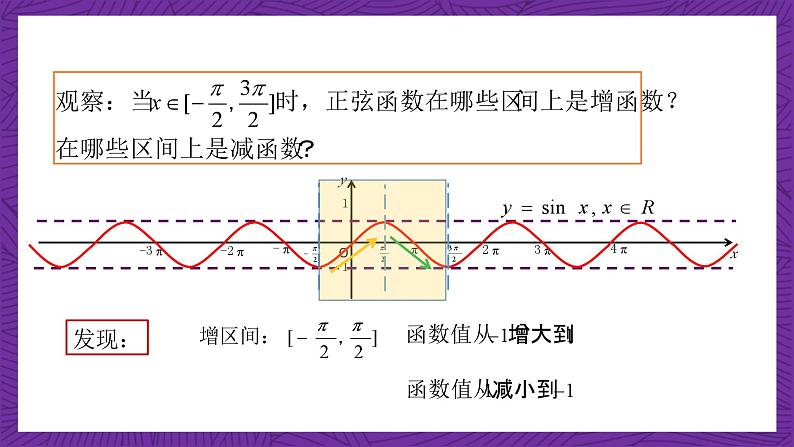
利用研究函数的经验,可否从正弦函数的定义域、值域、周期性、奇偶性和单调性等方面来研究正弦函数的性质呢?
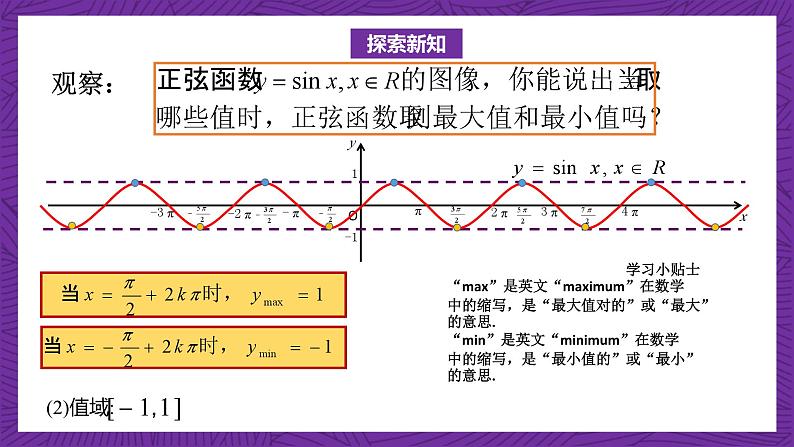
学习小贴士“max”是英文“maximum”在数学中的缩写,是“最大值对的”或“最大”的意思.“min”是英文“minimum”在数学中的缩写,是“最小值的”或“最小”的意思.
正弦函数y=sinx,x∈R的图像
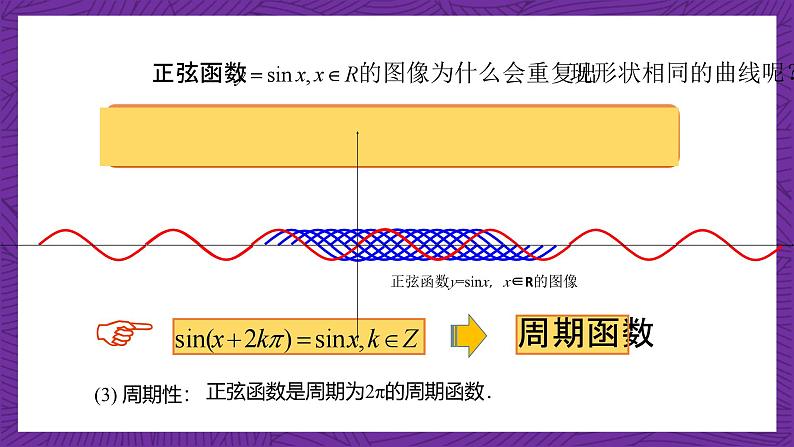
正弦函数是周期为2π的周期函数.
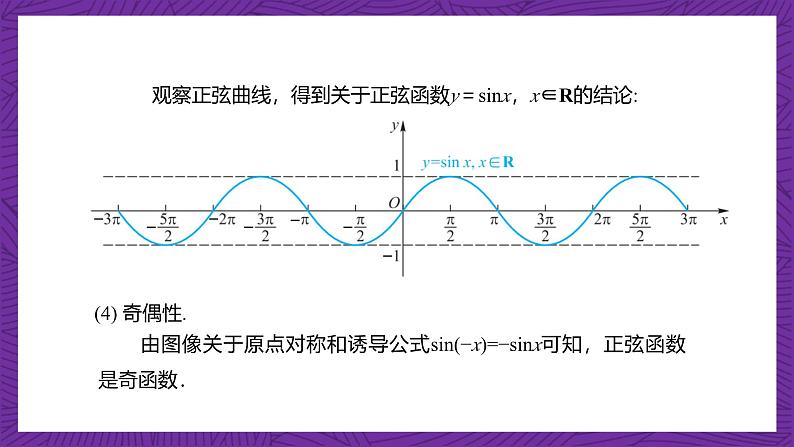
由图像关于原点对称和诱导公式sin(−x)=−sinx可知,正弦函数是奇函数.
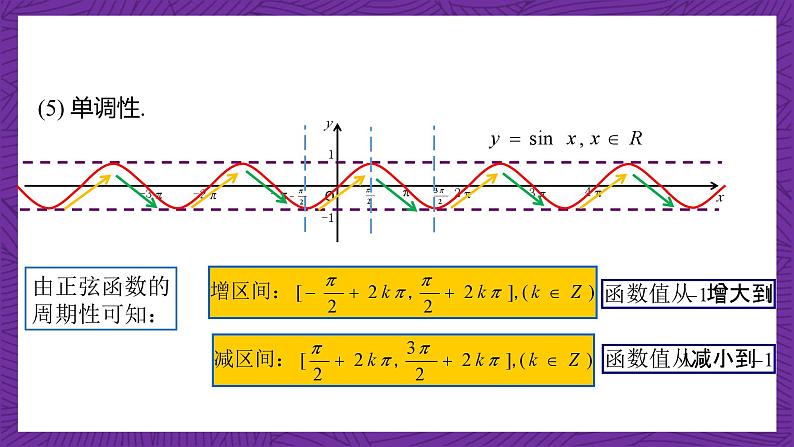
由正弦函数的周期性可知:
典例1 求下列函数的最大值和最小值,并写出取得最大值、最小值时自变量x的集合.
解 (1) 由正弦函数的性质知,-1≤sinx≤1,所以
(2)由正弦函数的性质知,-1≤sinx≤1,所以-2≤-2sinx≤2,-1≤1-2sinx≤3,即-1≤y≤3.故函数的最大值为3,最小值为-1.
使函数y=1-2sinx, x∈R取得最大值的x的集合, 就是使函数y=sinx, x∈R取得最小值的x的集合 ; 使函数y=1-2sinx, x∈R取得最小值的x的集合, 就是使函数y=sinx, x∈R取得最大值的x的集合 .
发现,在[0,2π]内, 符合题意的x 满足0≤x≤π.由函数的周期性得:
在[0,2π]内, 符合题意的 x 满足0≤x≤π.由函数的周期性得: 2kπ≤x≤π+2kπ(k∈Z),故函数的定义域为{x|2kπ≤x≤π+2kπ,k∈Z}.
对含三角函数的函数式求定义域时,除了考虑函数式有意义之外,还要注意三角函数的周期性.
【巩固2】比较下列各对正弦值的大小:
【巩固3】观察正弦曲线,写出满足下列条件的x的值:
巩固作业: P186练习4. 6.2;P190习题4.6.
利用研究函数的经验,可否从正弦函数的定义域、值域、周期性、奇偶性和单调性等方面来研究正弦函数的性质呢?
学习小贴士“max”是英文“maximum”在数学中的缩写,是“最大值对的”或“最大”的意思.“min”是英文“minimum”在数学中的缩写,是“最小值的”或“最小”的意思.
正弦函数y=sinx,x∈R的图像
正弦函数是周期为2π的周期函数.
由图像关于原点对称和诱导公式sin(−x)=−sinx可知,正弦函数是奇函数.
由正弦函数的周期性可知:
典例1 求下列函数的最大值和最小值,并写出取得最大值、最小值时自变量x的集合.
解 (1) 由正弦函数的性质知,-1≤sinx≤1,所以
(2)由正弦函数的性质知,-1≤sinx≤1,所以-2≤-2sinx≤2,-1≤1-2sinx≤3,即-1≤y≤3.故函数的最大值为3,最小值为-1.
使函数y=1-2sinx, x∈R取得最大值的x的集合, 就是使函数y=sinx, x∈R取得最小值的x的集合 ; 使函数y=1-2sinx, x∈R取得最小值的x的集合, 就是使函数y=sinx, x∈R取得最大值的x的集合 .
发现,在[0,2π]内, 符合题意的x 满足0≤x≤π.由函数的周期性得:
在[0,2π]内, 符合题意的 x 满足0≤x≤π.由函数的周期性得: 2kπ≤x≤π+2kπ(k∈Z),故函数的定义域为{x|2kπ≤x≤π+2kπ,k∈Z}.
对含三角函数的函数式求定义域时,除了考虑函数式有意义之外,还要注意三角函数的周期性.
【巩固2】比较下列各对正弦值的大小:
【巩固3】观察正弦曲线,写出满足下列条件的x的值:
巩固作业: P186练习4. 6.2;P190习题4.6.












