初中数学浙教版（2024）七年级上册5.4 一元一次方程的应用评优课课件ppt

这是一份初中数学浙教版（2024）七年级上册5.4 一元一次方程的应用评优课课件ppt，文件包含浙教版数学七上543《一元一次方程的应用》课件ppt、浙教版数学七上543《一元一次方程的应用》学案docx等2份课件配套教学资源，其中PPT共16页， 欢迎下载使用。

例5 学校组织植树活动，已知在甲处植树的有23人，在乙处植树的有17人，现调20人去支援，使在甲处植树的人数是乙处植树人数的2倍，应调往甲、乙两处各多少人？
分析 : 设应调往甲处x人，题目中涉及的有关数量及其关系能用表格去表示吗？
甲处增加后人数=2×乙处增加后人数
解：设应调往甲处x人，根据题意，得 23＋x＝2（17＋20－x） 解这个方程，得x＝17 ∴20-x＝3 答:应调往甲处17人，乙处3人。
想一想：若设调往乙处的人数为x，方程又应怎样列?
23+20-x＝2（17＋x）
在解决实际问题时,我们一般可以通过分析实际问题, 抽象出数学问题, 然后运用数学思想方法解决问题.用列表分析数量关系是常用的方法.
练习：学校组织初三年级100名团员去参加植树活动，如果挖坑，一天每人能挖树坑3个；如果植树，一天每人能植树7棵，要使每个树坑恰好能种上一棵树，问应安排几个人去挖坑，几个人去种树？
1、甲每天生产某种零件80个，3天能生产 个零件。2、乙每天生产某种零件x个，5天能生产 个零件。3、甲每天生产某种零件80个，乙每天生产某种零件x个。 他们5天一共生产 个零件。4、甲每天生产某种零件80个，乙每天生产这种零件x个 甲生产3天后，乙也加入生产同一种零件，再经过5天， 两人共生产 个零件。
工程问题的基本数量关系：
工作总量=工作时间×工作效率
(3×80+5×80+5x)
5、一批零件，甲每小时能加工80个，则　　⑴甲3小时可加工____个零件，x小时可加工____个零件。⑵加工a个零件，甲需______小时完成。6、一项工程甲独做需6天完成，则⑴甲独做一天可完成这项工程的________⑵若乙独做比甲快2天完成，则乙独做一天可完成　这项工程的__________
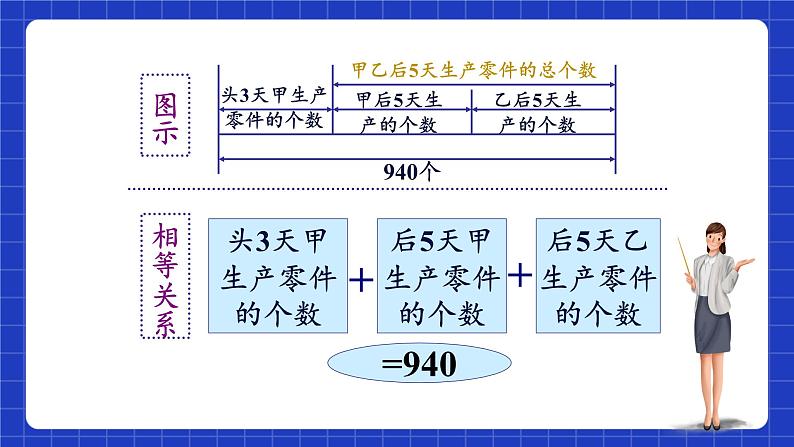
例6：甲每天生产某种零件80个，甲生产3天后，乙也加入生产同一种零件，再经过5天，两人共生产这种零件940个，问乙每天生产这种零件多少个？
头3天甲生产零件的个数
甲乙后5天生产零件的总个数
后5天甲生产零件的个数
后5天乙生产零件的个数
对于数量关系较为复杂的应用题，我们经常采用的方法是：先画出示意图（图示法）使题目中的条件和结论变得直观明显；然后建立方程。
练习：一件工作，甲单独做20个小时完成，乙单独做12小时完成，现在先由甲单独做4小时，剩下的部分由甲、乙合做。剩下的部分需要几小时完成？
甲先做4小时完成的工做量
合做x小时甲完成的工作量
合做x小时乙完成的工作量
相等关系：全部工作量＝甲独做工作量＋甲、乙合作工作量
设甲、乙合做部分需要x小时完成，甲独做部分完成的工作量为甲、乙合做部分完成的工作量为
某装潢公司接到一项业务，如果由甲组需10天完成，由乙组做需15天完成.为了早日完工，现由甲、乙两组一起做，4天后甲组因另有任务，余下部分由乙组单独做，问还需几天才能完成？
(1)可否用示意图来分析数量关系?
(2)总工作量怎么表示?甲乙两人的工作 效率怎么表示?
(3)设哪个未知数?相关的量怎样用它表示?
(4)根据怎样的数量关系列方程?
1.一件商品的销售价为100元，买入价为90元，则毛利润为 元。2.某商品的原价是x元，若按七五折出售，售价是 。3.一件夹克成本价为50元，提价50％后标价，再按标价的8折出售，则售价为 元。
成本价(进价或本金)：
商家取得某一商品所需要付出的金额。
商家出售商品时所标明的价格。
指商品成交时的实际价格；
指商品售价与进价之间的差额，即： 利润=售价－进价
指利润与成本的比率，即： 利润率 ＝
1、一件商品的进价为45元，利润为10元， 则售价为 ；
2、一件商品的标价为50元，现以八折销售，则售价为 ，若进价为33元，则它的利润为 ;
3、一块手表的成本价是70元，利润率是30％，则这　块手表的利润是 ，售价是 ;　　　　　　
4、某商品的原价是a元，提价10％后再降价10％，　这时这件商品的价格是(　　)