四川省巴中市巴州区2023-2024学年九年级上学期期中数学试卷

这是一份四川省巴中市巴州区2023-2024学年九年级上学期期中数学试卷，共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（4分）已知菱形的两条对角线长分别是6和8，则菱形的面积是（ ）
A．48B．30C．24D．20
2．（4分）若，则的值为（ ）
A．B．﹣7C．D．7
3．（4分）将一元二次方程x2﹣2x﹣2＝0配方后所得的方程是（ ）
A．（x﹣2）2＝2B．（x﹣1）2＝2C．（x﹣1）2＝3D．（x﹣2）2＝3
4．（4分）如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（ ）
A．B．
C．D．
5．（4分）下列命题是假命题的是（ ）
A．对角线相等、垂直的平行四边形是正方形
B．对角线相等的平行四边形是矩形
C．对角线垂直的四边形是菱形
D．对角线互相平分的四边形是平行四边形
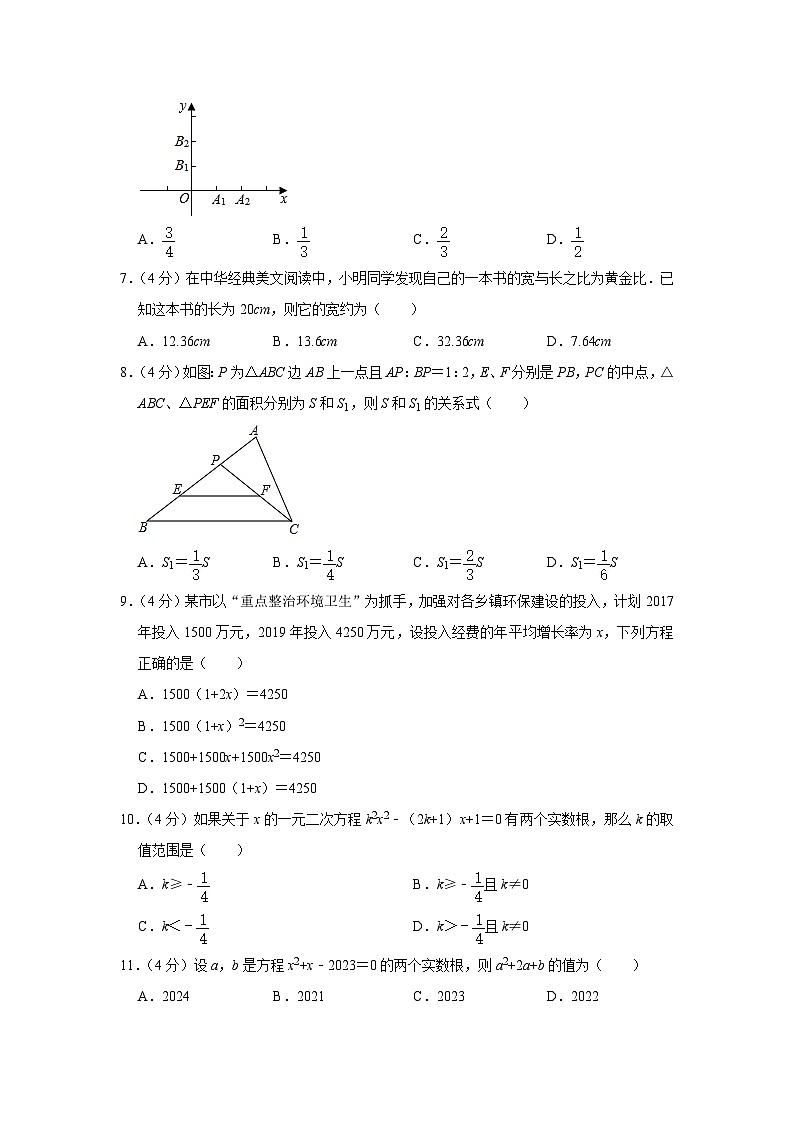
6．（4分）如图，在平面直角坐标系中，点A1，A2在x轴上，点B1，B2在y轴上，其坐标分别为A1（1，0），A2（2，0），B1（0，1），B2（0，2），分别以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形，所作三角形是等腰三角形的概率是（ ）
A．B．C．D．
7．（4分）在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比．已知这本书的长为20cm，则它的宽约为（ ）
A．12.36cmB．13.6cmC．32.36cmD．7.64cm
8．（4分）如图：P为△ABC边AB上一点且AP：BP＝1：2，E、F分别是PB，PC的中点，△ABC、△PEF的面积分别为S和S1，则S和S1的关系式（ ）
A．S1＝SB．S1＝SC．S1＝SD．S1＝S
9．（4分）某市以“重点整治环境卫生”为抓手，加强对各乡镇环保建设的投入，计划2017年投入1500万元，2019年投入4250万元，设投入经费的年平均增长率为x，下列方程正确的是（ ）
A．1500（1+2x）＝4250
B．1500（1+x）2＝4250
C．1500+1500x+1500x2＝4250
D．1500+1500（1+x）＝4250
10．（4分）如果关于x的一元二次方程k2x2﹣（2k+1）x+1＝0有两个实数根，那么k的取值范围是（ ）
A．k≥﹣B．k≥﹣且k≠0
C．k＜﹣D．k＞﹣且k≠0
11．（4分）设a，b是方程x2+x﹣2023＝0的两个实数根，则a2+2a+b的值为（ ）
A．2024B．2021C．2023D．2022
12．（4分）如图，在▱ABCD中，E是BA延长线上一点，CE分别与AD，BD交于点G，F．则下列结论：
①；②；③；④CF2＝GF•EF．
其中正确的是（ ）
A．①②③④B．①②③C．①③④D．①②
二、填空题（每小题3分，共18分）
13．（3分）关于x的方程x2﹣kx﹣6＝0有一根为x＝﹣3，则k的值为 ．
14．（3分）已知△ABC∽△A1B1C1，且它们的面积比为1：4，则AB：A1B1＝ ．
15．（3分）对于实数m、n，定义运算“⊗”如下：m⊗n＝m2﹣2mn．若（x+1）⊗（x﹣2）＝5，则x的值为 ．
16．（3分）如图，矩形OBCD的顶点C的坐标为（1，3），则线段BD的长等于 ．
17．（3分）如图，将边长为6的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在点Q处，EQ与BC交于点G，则△EBG的周长是 cm．
18．（3分）如图所示，在△ABC中，BC＝6，E、F分别是AB、AC的中点，动点P在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ＝CE时，EP+BP＝ ．
三、解答题（共84分．解答应写出必要的文字说明、证明过程或演算步骤）
19．（18分）计算．
（1）计算：；
（2）解方程：2x2﹣5x﹣1＝0；
（3）先化简，再求值：，其中a满足a2+2a﹣5＝0．
20．（10分）已知关于x的一元二次方程x2+2（m+1）x+m2﹣1＝0．
（1）若方程有实数根，求实数m的取值范围；
（2）若方程两实数根分别为x1，x2，且满足（x1﹣x2）2＝16﹣x1x2，求实数m的值．
21．（10分）某商场为掌握国庆节期间顾客购买商品时刻的分布情况，统计了10月1日7：00﹣23：00这一时间段内5000名顾客的购买时刻．顾客购买商品时刻的频数分布直方图和扇形统计图如图所示，将7：00﹣23：00这一时间段划分为四个小的时间段：A段为7：00≤t＜11：00，B段为11：00≤t＜15：00，C段为15：00≤t＜19：00，D段为19：00≤t≤23：00，其中t为顾客购买商品的时刻，扇形统计图中，A，B，C，D四段各部分圆心角的度数比为1：3：4：2．
请根据上述信息解答下列问题：
（1）通过计算将频数分布直方图补充完整，并直接写出顾客购买商品时刻的中位数落在哪个时间段？
（2）求10月1日这天顾客购买商品时刻的平均值（同一时间段内顾客购买商品时刻的平均值用该时段的中点值代表，例如，A段的中点值为：＝9）；
（3）为活跃节日气氛，该商场设置购物后抽奖活动，设立了特等奖一个，一等奖两个，二等奖若干，并随机分配到A，B，C，D四个时间段中．
①请直接写出特等奖出现在A时间段的概率；
②请利用画树状图或列表的方法，求两个一等奖出现在不同时间段的概率．
22．（10分）如图为住宅区内的两幢楼，它们的高AB＝CD＝30m，现需了解甲楼对乙楼的采光的影响情况．当太阳光与水平线的夹角为30°时．试求：
（1）若两楼间的距离AC＝24m时，甲楼的影子，落在乙楼上有多高？
（2）若甲楼的影子，刚好不影响乙楼，那么两楼的距离应当有多远？
23．（10分）某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件．
（1）降价前商场每月销售该商品的利润是多少元？
（2）要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？
24．（12分）如图，AB∥CD，且AB＝2CD，E是AB的中点，F是边BC上的动点，EF与BD相交于点M．
（1）求证：△EDM∽△FBM；
（2）若F是BC的中点，BD＝12，求BM的长；
（3）若AD＝BC，BD平分∠ABC，点P是线段BD上的动点，是否存在点P使DP•BP＝BF•CD，若存在，求出∠CPF的度数；若不存在，请说明理由．
25．（14分）如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2﹣7x+12＝0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．
（1）求A、B两点的坐标；
（2）求当t为何值时，△APQ与△AOB相似；
（3）当t＝2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．
参考答案与试题解析
一、选择题（本大题共12小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．（4分）已知菱形的两条对角线长分别是6和8，则菱形的面积是（ ）
A．48B．30C．24D．20
【分析】根据菱形的面积等于两条对角线积的一半计算即可．
【解答】解：∵菱形的两条对角线长分别是6和8，
∴这个菱形的面积为×6×8＝24，
故选：C．
【点评】本题考查了菱形的面积的计算等知识点．易错易混点：学生在求菱形面积时，易把对角线乘积当成菱形的面积，或是错误判断对角线的长而误选
2．（4分）若，则的值为（ ）
A．B．﹣7C．D．7
【分析】设＝k，则a＝3k，b＝4k，c＝5k，代入式子计算即可．
【解答】解：设＝k，则a＝3k，b＝4k，c＝5k，
∴＝＝＝﹣7．
故选：B．
【点评】本题考查了比例的性质，熟练掌握比例的性质是关键．
3．（4分）将一元二次方程x2﹣2x﹣2＝0配方后所得的方程是（ ）
A．（x﹣2）2＝2B．（x﹣1）2＝2C．（x﹣1）2＝3D．（x﹣2）2＝3
【分析】配方法解一元二次方程，解题时要注意解题步骤的准确使用，把左边配成完全平方式，右边化为常数．
【解答】解：∵x2﹣2x﹣2＝0，
∴x2﹣2x＝2，
∴x2﹣2x+1＝2+1，
∴（x﹣1）2＝3．
故选：C．
【点评】本题考查了配方法解一元二次方程．配方法的一般步骤：
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
4．（4分）如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（ ）
A．B．
C．D．
【分析】根据网格中的数据求出AB，AC，BC的长，求出三边之比，利用三边对应成比例的两三角形相似判断即可．
【解答】解：根据题意得：AB＝＝，AC＝，BC＝2，
∴AC：BC：AB＝：2：＝1：：，
A、三边之比为1：：2，图中的三角形（阴影部分）与△ABC不相似；
B、三边之比为：：3，图中的三角形（阴影部分）与△ABC不相似；
C、三边之比为1：：，图中的三角形（阴影部分）与△ABC相似；
D、三边之比为2：：，图中的三角形（阴影部分）与△ABC不相似．
故选：C．
【点评】此题考查了相似三角形的判定，熟练掌握相似三角形的判定方法是解本题的关键．
5．（4分）下列命题是假命题的是（ ）
A．对角线相等、垂直的平行四边形是正方形
B．对角线相等的平行四边形是矩形
C．对角线垂直的四边形是菱形
D．对角线互相平分的四边形是平行四边形
【分析】根据正方形、矩形、菱形、平行四边形的判定方法即可得出结论．
【解答】解：A、对角线相等、垂直的平行四边形是正方形；真命题；
B、对角线相等的平行四边形是矩形；真命题；
C、对角线垂直的四边形是菱形；假命题；
D、对角线互相平分的四边形是平行四边形；真命题；
故选：C．
【点评】本题考查了命题与定理；熟记正方形、矩形、菱形、平行四边形的判定方法是解决问题的关键．
6．（4分）如图，在平面直角坐标系中，点A1，A2在x轴上，点B1，B2在y轴上，其坐标分别为A1（1，0），A2（2，0），B1（0，1），B2（0，2），分别以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形，所作三角形是等腰三角形的概率是（ ）
A．B．C．D．
【分析】根据题意画出树状图，进而得出以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形是等腰三角形的情况，求出概率即可．
【解答】解：∵以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形，
∴画树状图得：
共可以组成4个三角形，
所作三角形是等腰三角形只有：△OA1B1，△OA2B2，
所作三角形是等腰三角形的概率是：＝．
故选：D．
【点评】此题主要考查了利用树状图求概率以及等腰三角形的判定等知识，利用树状图表示出所有可能是解题关键．
7．（4分）在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比．已知这本书的长为20cm，则它的宽约为（ ）
A．12.36cmB．13.6cmC．32.36cmD．7.64cm
【分析】把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值（）叫做黄金比．
【解答】解：方法1：设书的宽为x，则有（20+x）：20＝20：x，解得x＝12.36cm．
方法2：书的宽为20×0.618＝12.36cm．
故选：A．
【点评】理解黄金分割的概念，找出黄金分割中成比例的对应线段是解决问题的关键．
8．（4分）如图：P为△ABC边AB上一点且AP：BP＝1：2，E、F分别是PB，PC的中点，△ABC、△PEF的面积分别为S和S1，则S和S1的关系式（ ）
A．S1＝SB．S1＝SC．S1＝SD．S1＝S
【分析】先利用三角形中位线的性质得到EF∥BC，EF＝BC，则可判断△PEF∽△PBC，利用相似三角形的性质得＝，接着利用三角形面积公式得到S△PBC：S△PAC＝2：1，所以S△PBC＝2S1，于是得到S＝6S1．
【解答】解：∵E、F分别是PB，PC的中点，
∴EF∥BC，EF＝BC，
∴△PEF∽△PBC，
∴＝（）2＝（）2＝，
即S△PBC＝4S1，
∵AP：BP＝1：2，
∴S△PBC：S△PAC＝2：1，
∴S△PBC＝2S1，
∴S＝4S1+2S1＝6S1，
即S1＝S．
故选：D．
【点评】三本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；在利用相似三角形的性质时，主要利用相似比计算线段的长或利用相似比表示面积之间的关系．
9．（4分）某市以“重点整治环境卫生”为抓手，加强对各乡镇环保建设的投入，计划2017年投入1500万元，2019年投入4250万元，设投入经费的年平均增长率为x，下列方程正确的是（ ）
A．1500（1+2x）＝4250
B．1500（1+x）2＝4250
C．1500+1500x+1500x2＝4250
D．1500+1500（1+x）＝4250
【分析】增长率为x可得2018年投入为1500（1+x），则2019年的投入为1500（1+x）（1+x），在正确列出方程即可．
【解答】解：2017年投入1500万元，增长率为x，
∴2018年投入为1500（1+x），
∴2019年投入为1500（1+x）（1+x）＝1500（1+x）2，
∵2019年投入4250万元，
∴可列方程为1500（1+x）2＝4250，
故选：B．
【点评】本题主要考查一元二次方程中增长率问题的应用，解题的关键在于明确从2017年到2019年连续增长两次．
10．（4分）如果关于x的一元二次方程k2x2﹣（2k+1）x+1＝0有两个实数根，那么k的取值范围是（ ）
A．k≥﹣B．k≥﹣且k≠0
C．k＜﹣D．k＞﹣且k≠0
【分析】根据一元二次方程的定义以及根的判别式的意义得出k2≠0，且Δ＝b2﹣4ac≥0，建立关于k的不等式组，求出k的取值范围．
【解答】解：由题意知，k2≠0，且Δ＝b2﹣4ac＝（2k+1）2﹣4k2＝4k+1≥0．
解得k≥﹣且k≠0．
故选：B．
【点评】本题考查了一元二次方程ax2+bx+c＝0（a≠0）的根的判别式Δ＝b2﹣4ac：当Δ＞0，方程有两个不相等的实数根；当Δ＝0，方程有两个相等的实数根；当Δ＜0，方程没有实数根．也考查了一元二次方程的定义．
11．（4分）设a，b是方程x2+x﹣2023＝0的两个实数根，则a2+2a+b的值为（ ）
A．2024B．2021C．2023D．2022
【分析】先根据一元二次方程的解的定义得到a2＝﹣a+2023，则a2+2a+b可化为2023+a+b，再根据根与系数的关系得到a+b＝﹣1，然后利用整体代入的方法计算．
【解答】解：∵a是方程x2+x﹣2023＝0的实数根，
∴a2+a﹣2023＝0，
∴a2＝﹣a+2023，
∴a2+2a+b＝﹣a+2023+2a+b＝2023+a+b，
∵a，b是方程x2+x﹣2023＝0的两个实数根，
∴a+b＝﹣1，
∴a2+2a+b＝2023+（﹣1）＝2022．
故选：D．
【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝．也考查了一元二次方程的解．
12．（4分）如图，在▱ABCD中，E是BA延长线上一点，CE分别与AD，BD交于点G，F．则下列结论：
①；②；③；④CF2＝GF•EF．
其中正确的是（ ）
A．①②③④B．①②③C．①③④D．①②
【分析】根据平行四边形的性质和平行线分线段成比例定理即可解决问题．
【解答】解：∵四边形ABCD是平行四边形，
∴BE∥CD，AD∥BC，
∴＝，故①正确，
∴＝，故②正确，
＝，故③正确，
∵＝＝，
∴CF2＝EF•GF，故④正确，
故选：A．
【点评】本题考查平行四边形的性质，平行线分线段成比例定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
二、填空题（每小题3分，共18分）
13．（3分）关于x的方程x2﹣kx﹣6＝0有一根为x＝﹣3，则k的值为 ﹣1 ．
【分析】把x＝﹣3代入已知方程，列出关于k的新方程，通过解新方程来求k的值．
【解答】解：∵关于x的一元二次方程x2﹣kx﹣6＝0有一个根是x＝﹣3，
∴9+3k﹣6＝0，
解得：k＝﹣1，
故答案为：﹣1．
【点评】本题考查了一元二次方程的解的定义．能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
14．（3分）已知△ABC∽△A1B1C1，且它们的面积比为1：4，则AB：A1B1＝ 1：2 ．
【分析】根据相似三角形的面积比等于相似比的平方求解即可求得答案．
【解答】解：∵△ABC∽△A′B′C′且它们的面积比为1：4，
∴AB：A′B′＝1：2．
故答案为：1：2．
【点评】此题考查了相似三角形的性质．此题比较简单，注意掌握相似三角形的面积比等于相似比的平方．
15．（3分）对于实数m、n，定义运算“⊗”如下：m⊗n＝m2﹣2mn．若（x+1）⊗（x﹣2）＝5，则x的值为 0或4 ．
【分析】由题意列式并整理可得一元二次方程，解方程即可．
【解答】解：由题意可得（x+1）2﹣2（x+1）（x﹣2）＝5，
整理得：x2﹣4x＝0，
解得：x＝0或x＝4，
故答案为：0或4．
【点评】本题考查解一元二次方程，结合已知条件列得正确的方程是解题的关键．
16．（3分）如图，矩形OBCD的顶点C的坐标为（1，3），则线段BD的长等于 ．
【分析】先根据勾股定理求出OC，再由矩形的对角线相等即可得出结果．
【解答】解：连接OC，BD，如图所示：
根据勾股定理得：OC＝＝，
∵四边形OBCD是矩形，
∴BD＝OC＝；
故答案为：．
【点评】本题考查了矩形的性质、坐标与图形性质、勾股定理；熟练掌握矩形的性质，运用勾股定理求出OC是解决问题的关键．
17．（3分）如图，将边长为6的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在点Q处，EQ与BC交于点G，则△EBG的周长是 12 cm．
【分析】根据翻折的性质可得DF＝EF，设EF＝x，表示出AF，然后利用勾股定理列方程求出x，从而得到AF、EF的长，再求出△AEF和△BGE相似，根据相似三角形对应边成比例列式求出BG、EG，然后根据三角形周长的定义列式计算即可得解．
【解答】解：由翻折的性质得，DF＝EF，
设EF＝x，则AF＝6﹣x，
∵点E是AB的中点，
∴AE＝BE＝×6＝3，
在Rt△AEF中，AE2+AF2＝EF2，
即32+（6﹣x）2＝x2，
解得x＝，
∴AF＝6﹣＝，
∵∠FEG＝∠D＝90°，
∴∠AEF+∠BEG＝90°，
∵∠AEF+∠AFE＝90°，
∴∠AFE＝∠BEG，
又∵∠A＝∠B＝90°，
∴△AEF∽△BGE，
∴＝＝，
即＝＝，
解得BG＝4，EG＝5，
∴△EBG的周长＝3+4+5＝12（cm）．
故答案为：12．
【点评】本题考查了翻折变换的性质，勾股定理，相似三角形的判定与性质，熟记性质并求出△AEF的各边的长，然后利用相似三角形的性质求出△EBG的各边的长是解题的关键，也是本题的难点．
18．（3分）如图所示，在△ABC中，BC＝6，E、F分别是AB、AC的中点，动点P在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ＝CE时，EP+BP＝ 12 ．
【分析】延长BQ交射线EF于M，根据三角形的中位线平行于第三边可得EF∥BC，根据两直线平行，内错角相等可得∠M＝∠CBM，再根据角平分线的定义可得∠PBM＝∠CBM，从而得到∠M＝∠PBM，根据等角对等边可得BP＝PM，求出EP+BP＝EM，再根据CQ＝CE求出EQ＝2CQ，然后根据△MEQ和△BCQ相似，利用相似三角形对应边成比例列式求解即可．
【解答】解：如图，延长BQ交射线EF于M，
∵E、F分别是AB、AC的中点，
∴EF∥BC，
∴∠M＝∠CBM，
∵BQ是∠CBP的平分线，
∴∠PBM＝∠CBM，
∴∠M＝∠PBM，
∴BP＝PM，
∴EP+BP＝EP+PM＝EM，
∵CQ＝CE，
∴EQ＝2CQ，
由EF∥BC得，△MEQ∽△BCQ，
∴＝＝2，
∴EM＝2BC＝2×6＝12，
即EP+BP＝12．
故答案为：12．
【点评】本题考查了相似三角形的判定与性质，角平分线的定义，平行线的性质，延长BQ构造出相似三角形，求出EP+BP＝EM并得到相似三角形是解题的关键，也是本题的难点．
三、解答题（共84分．解答应写出必要的文字说明、证明过程或演算步骤）
19．（18分）计算．
（1）计算：；
（2）解方程：2x2﹣5x﹣1＝0；
（3）先化简，再求值：，其中a满足a2+2a﹣5＝0．
【分析】（1）根据绝对值的性质、二次根式的化简、负整数次幂的意义进行计算即可；
（2）利用公式法求解即可；
（3）根据分式的混合运算法则把原式化简，由a2+2a﹣5＝0，得a（a+2）＝5，代入计算得到答案．
【解答】解：（1）原式＝﹣3++4
＝3﹣；
（2）2x2﹣5x﹣1＝0，
这里a＝2，b＝﹣5，c＝﹣1，
∴Δ＝（﹣5）2﹣4×2×（﹣1）＝33＞0，
∴x＝＝，
∴x1＝，x2＝；
（3）
＝（﹣）•
＝
＝2a（a+2），
由a2+2a﹣5＝0，得a（a+2）＝5，
∴原式＝2×5＝10．
【点评】本题考查解一元二次方程，二次根式的混合运算，分式的化简求值，掌握分式的混合运算法则，二次根式混合运算的法则及一元二次方程的求解方法是解题关键．
20．（10分）已知关于x的一元二次方程x2+2（m+1）x+m2﹣1＝0．
（1）若方程有实数根，求实数m的取值范围；
（2）若方程两实数根分别为x1，x2，且满足（x1﹣x2）2＝16﹣x1x2，求实数m的值．
【分析】（1）若一元二次方程有两实数根，则根的判别式Δ＝b2﹣4ac≥0，建立关于m的不等式，求出m的取值范围；
（2）由x1+x2＝﹣2（m+1），x1x2＝m2﹣1；代入（x1﹣x2）2＝16﹣x1x2，建立关于m的方程，据此即可求得m的值．
【解答】解：（1）由题意有Δ＝[2（m+1）]2﹣4（m2﹣1）≥0，
整理得8m+8≥0，
解得m≥﹣1，
∴实数m的取值范围是m≥﹣1；
（2）由两根关系，得x1+x2＝﹣2（m+1），x1•x2＝m2﹣1，
（x1﹣x2）2＝16﹣x1x2
（x1+x2）2﹣3x1x2﹣16＝0，
∴[﹣2（m+1）]2﹣3（m2﹣1）﹣16＝0，
∴m2+8m﹣9＝0，
解得m＝﹣9或m＝1
∵m≥﹣1
∴m＝1．
【点评】本题考查了一元二次方程根的判别式及根与系数关系，利用两根关系得出的结果必须满足△≥0的条件．
21．（10分）某商场为掌握国庆节期间顾客购买商品时刻的分布情况，统计了10月1日7：00﹣23：00这一时间段内5000名顾客的购买时刻．顾客购买商品时刻的频数分布直方图和扇形统计图如图所示，将7：00﹣23：00这一时间段划分为四个小的时间段：A段为7：00≤t＜11：00，B段为11：00≤t＜15：00，C段为15：00≤t＜19：00，D段为19：00≤t≤23：00，其中t为顾客购买商品的时刻，扇形统计图中，A，B，C，D四段各部分圆心角的度数比为1：3：4：2．
请根据上述信息解答下列问题：
（1）通过计算将频数分布直方图补充完整，并直接写出顾客购买商品时刻的中位数落在哪个时间段？
（2）求10月1日这天顾客购买商品时刻的平均值（同一时间段内顾客购买商品时刻的平均值用该时段的中点值代表，例如，A段的中点值为：＝9）；
（3）为活跃节日气氛，该商场设置购物后抽奖活动，设立了特等奖一个，一等奖两个，二等奖若干，并随机分配到A，B，C，D四个时间段中．
①请直接写出特等奖出现在A时间段的概率；
②请利用画树状图或列表的方法，求两个一等奖出现在不同时间段的概率．
【分析】（1）根据圆心角的比算出各部分的数量，补全频数分布直方图即可；按照时间段从早到晚进行排序，根据各部分的人数推断出排在中间第2500和2501名所在的时间段即可得出中位数所处的时间段；
（2）按照加权平均数的计算公式计算即可；
（3）①直接根据概率公式进行计算即可；
②先画树状图，然后再利用概率公式进行计算即可．
【解答】解：（1）∵扇形统计图中，A，B，C，D四段各部分圆心角的度数比为1：3：4：2，
∴B段的顾客人数为5000×＝1500（人），C段的顾客人数为5000×＝2000（人），
故补全的统计图如下，
∴中位数落在C段：15：00≤t＜19：00；
（2）（500×9+1500×13+2000×17+21×1000）÷5000＝15.8，
所以，10月1日这天顾客购买商品时刻的平均值为15.8；
（3）
①特等奖出现在A时间段的概率为；
②根据题意，树状图如下：
总共有16种等可能的结果，两个一等奖出现在不同时间段的情况有12种，
故两个一等奖出现在不同时间段的概率是＝．
【点评】本题主要考查了频数分布直方图与扇形统计图的结合，列表或画树状图求概率，根据题意画出树状图或列出表格是解题的关键．
22．（10分）如图为住宅区内的两幢楼，它们的高AB＝CD＝30m，现需了解甲楼对乙楼的采光的影响情况．当太阳光与水平线的夹角为30°时．试求：
（1）若两楼间的距离AC＝24m时，甲楼的影子，落在乙楼上有多高？
（2）若甲楼的影子，刚好不影响乙楼，那么两楼的距离应当有多远？
【分析】（1）首先设太阳光与CD的交点为E，连接BD，易得四边形ABCD是矩形，然后在Rt△BDE中，由DE＝BD•tan30°即可求得答案；
（2）首先根据题意可得当太阳光照射到点C时，甲楼的影子，刚好不影响乙楼，然后由AC＝，即可求得答案．
【解答】解：（1）设太阳光与CD的交点为E，连接BD，
∵AB＝CD＝30m，BA⊥AC，CD⊥AC，
∴四边形ABCD是矩形，
∴BD＝AC＝24m，∠BDE＝90°，
∵∠DBE＝30°，
∴在Rt△BDE中，DE＝BD•tan30°＝24×＝8（m），
∴EC＝CD﹣DE＝30﹣8（m）．
答：甲楼的影子，落在乙楼上有（30﹣8）m高；
（2）如图：当太阳光照射到点C时，甲楼的影子，刚好不影响乙楼，
在Rt△ABC中，AB＝30m，∠ACB＝30°，
∴AC＝＝30÷＝30（m）．
答：两楼的距离应当为30m．
【点评】此题考查了解直角三角形的应用．此题难度适中，注意能根据题意构造直角三角形，并能借助于解直角三角形的知识求解是解此题的关键．
23．（10分）某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件．
（1）降价前商场每月销售该商品的利润是多少元？
（2）要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？
【分析】（1）先求出每件的利润．再乘以每月销售的数量就可以得出每月的总利润；（2）设要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价x元，由销售问题的数量关系建立方程求出其解即可．
【解答】解：（1）由题意，得60（360﹣280）＝4800（元）．
答：降价前商场每月销售该商品的利润是4800元；
（2）设要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价x元，
由题意，得（360﹣x﹣280）（5x+60）＝7200，
解得：x1＝8，x2＝60．
∵有利于减少库存，
∴x＝60．
答：要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价60元．
【点评】本题考查了销售问题的数量关系利润＝售价﹣进价的运用，列一元二次方程解实际问题的运用，解答时根据销售问题的数量关系建立方程是关键．
24．（12分）如图，AB∥CD，且AB＝2CD，E是AB的中点，F是边BC上的动点，EF与BD相交于点M．
（1）求证：△EDM∽△FBM；
（2）若F是BC的中点，BD＝12，求BM的长；
（3）若AD＝BC，BD平分∠ABC，点P是线段BD上的动点，是否存在点P使DP•BP＝BF•CD，若存在，求出∠CPF的度数；若不存在，请说明理由．
【分析】（1）先证明四边形BCDE为平行四边形，从而得到ED∥BC，于是得到∠EDB＝∠FBM，又因为∠DME＝∠BMF，从而可证明△EDM∽△FBM；
（2）根据（1）中三角形相似的比例关系即可推理得出答案．
（3）存在，先证明△PDC∽△FBP，得∠BPF＝∠PCD，根据平角的定义和三角形的内角和定理可得：∠PDC＝∠CPF，再证△ADE是等边三角形，得∠AED＝60°，可得∠CPF＝30°．
【解答】（1）证明：∵AB＝2CD，点E是AB的中点，
∴DC＝EB．
又∵AB∥CD，
∴四边形BCDE为平行四边形．
∴ED∥BC．
∴∠EDB＝∠FBM．
又∵∠DME＝∠BMF，
∴△EDM∽△FBM；
（2）解：∵△EDM∽△FBM，
∴＝，
∵F是BC的中点，
∴DE＝BC＝2BF，
∴DM＝2BM，
∴DB＝DM+BM＝3BM，
∵DB＝12，
∴BM＝DB＝×12＝4；
（3）存在，∵DC∥AB，
∴∠CDB＝∠ABD，
∵BD平分∠ABC，
∴∠CBD＝∠ABD，
∴∠CDB＝∠CBD，
∴DC＝BC，
∵DP•BP＝BF•CD，
∴，
∴△PDC∽△FBP，
∴∠BPF＝∠PCD，
∵∠DPC+∠CPF+∠BPF＝180°，
∠DPC+∠PDC+∠PCD＝180°，
∴∠PDC＝∠CPF，
∵AD＝BC＝DC＝BE＝AE，
∴△ADE是等边三角形，
∴∠AED＝60°，
∴∠EDB＝∠PDC＝30°，
∴∠CPF＝30°．
【点评】本题主要考查的是相似三角形的性质和判定、平行四边形的性质和判定，掌握相似三角形的性质是解题的关键，第三问有难度，将所求的角转化为另一个∠BDC和∠AED是解决问题的关键．
25．（14分）如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2﹣7x+12＝0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．
（1）求A、B两点的坐标；
（2）求当t为何值时，△APQ与△AOB相似；
（3）当t＝2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．
【分析】（1）解一元二次方程x2﹣7x+12＝0得到方程的两个根，结合OA＜OB确定OA、OB的长度，从而得到A、B点的坐标；
（2）由题意可知△APQ与△AOB相似时存在两种情况，即△APQ∽△AOB或△APQ∽△ABO，由（1）不难得到AP＝t、AQ＝5﹣2t，当△APQ∽△AOB，利用相似三角形的性质可得＝，于是可得t的值；根据OP＝OA﹣AP、PQ＝AP•tanA求出OP和PQ的长度，进而可以确定点Q的坐标．同理，还可求出△APQ∽△ABO时点Q的坐标；
（3）假设存在符合要求的点M，分三种情况进行分析，就能求出点M的坐标．
【解答】解：（1）∵x2﹣7x+12＝0，
∴（x﹣3）（x﹣4）＝0，
∴x﹣3＝0和x﹣4＝0，
得x1＝3，x2＝4．
∵OA＜OB，
∴OA＝3，OB＝4，
∴点A的坐标为（0，3），点B的坐标为（4，0）；
（2）∵OA＝3，OB＝4，∠AOB＝90°，
∴AB＝5，
∴AP＝t，BQ＝2t，AQ＝5﹣2t．
∵∠PAQ＝∠OAB，
∴△APQ与△AOB相似有两种情况．
当△APQ∽△AOB时，
∴＝，
∵OA＝3，AB＝5，AP＝t，AQ＝5﹣2t，
∴＝
∴t＝，
∴OP＝OA﹣AP＝，PQ＝AP•tanA＝，
∴点Q的坐标为（，）．
当△APQ∽△ABO时，过点Q作QH⊥y轴于点H，如图所示．
∴＝，
∵OA＝3，AB＝5，AP＝t，AQ＝5﹣2t，
∴＝，
∴t＝．
此时AQ＝，QH＝AQ×sin∠OAB＝，AH＝，
∴点Q的坐标为（，）．
综上所述，当t＝或t＝，△APQ与△AOB相似；
（3）存在，
理由：如图，由题意P（0，1），Q（，），
当四边形APMQ是平行四边形时，M（，），
当四边形APQM′是平行是斜边时，M′（，），
当四边形AQPM″是平行四边形时，设M″（x，y），则有，
解得，
∴M″（﹣，），
综上所述，点M的坐标为（，），（，）和（﹣，）．
【点评】本题属于相似形综合题，考查了相似三角形的判定和性质，平行四边形的判定和性质，一元二次方程等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考压轴题．