辽宁省盘锦市辽河油田实验中学2023-2024学年九年级下学期开学考试数学试题（原卷版+解析版）

这是一份辽宁省盘锦市辽河油田实验中学2023-2024学年九年级下学期开学考试数学试题（原卷版+解析版），文件包含辽宁省盘锦市辽河油田实验中学2023-2024学年九年级下学期开学考试数学试题原卷版docx、辽宁省盘锦市辽河油田实验中学2023-2024学年九年级下学期开学考试数学试题解析版docx等2份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。

1. 在东西向的马路上，把出发点记为0，向东与向西意义相反．若把向东走2km记作“+2km”，那么向西走1km应记作（ ）
A. ﹣2kmB. ﹣1kmC. +1kmD. +2km
【答案】B
【解析】
【分析】在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．
【详解】解：若把向东走2km记做“+2km”，那么向西走1km应记做﹣1km．
故选：B．
【点睛】本题主要考查正数与负数，理解正数与负数的意义是解题的关键．
2. 六个大小相同的正方体搭成的几何体如图所示，其主视图是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题主要考查了几何体的三视图，根据主视图是从正面看到的图形进行求解即可．
【详解】解；从正面看，看到的图形分为上下两层，共三列，从左边数，第一列下面一层有一个小正方形，第二列下面一层有一个小正方形，第三列上下两层各有一个小正方形，即看到的图形如下：
，
故选：A．
3. 古典园林中的花窗通常利用对称构图，体现对称美．下面四个花窗图案，既是轴对称图形又是中心对称图形的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据中心对称图形和轴对称图形定义进行解答即可．
【详解】解：A、是轴对称图形，不是中心对称图形，故此选项不符合题意；
B、既不是轴对称图形，也不是中心对称图形，故此选项不合题意；
C、既是轴对称图形，也是中心对称图形，故此选项符合题意；
D、是轴对称图形，不是中心对称图形，故此选项不合题意；
故选：C．
【点睛】此题主要考查了轴对称图形和中心对称图形定义，关键是掌握如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．
4. 下列计算结果正确的是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】本题主要考查了幂的乘方，积的乘方，同底数幂相除，完全平方公式．根据幂的乘方，积的乘方，同底数幂相除，完全平方公式，逐项判断即可求解．
【详解】解：A、，故本选项不符合题意；
B、，故本选项符合题意；
C、，故本选项不符合题意；
D、，故本选项不符合题意；
故选：B
5. 关于x的一元二次方程的根的情况是（ ）
A. 有两个不相等的实数根B. 有两个相等的实数根
C. 只有一个实数根D. 没有实数根
【答案】A
【解析】
【分析】本题考查的是根的判别式，熟知一元二次方程的根与的关系是解答此题的关键．先求出△的值，再判断出其符号即可．
【详解】解：，
方程有两个不等实根．
故选：A．
6. 不等式组的解集在数轴上表示正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】本题考查了解一元一次不等式组，在数轴上表示不等式的解集，先求出不等式组的解集，将解集在数轴上表示出来即可求解，熟练掌握解一元一次不等式组是解题的关键．
【详解】解：
解不等式①得，x>1，
解不等式②得：，
∴不等式组的解集为，
∴该不等式组的解集在数轴上表示如图所示：
故选：．
7. 我国古代数学著作《孙子算经》中记载“鸡兔同笼”问题：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？若设兔子有x只，鸡有y只，则下列方程组中正确的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题主要考查由实际问题抽象出二元一次方程组，根据鸡的数量加上兔的数量等于35，鸡的脚的数量加上兔子的脚的数量等于94可列方程组．
【详解】解：若设兔子有x只，鸡有y只，则兔有条腿，鸡有只脚，
根据题意，可列方程组为，
故选：D．
8. 如图，烧杯内液体表面与烧杯下底部平行，光线从液体中射向空气时发生折射，光线变成，点在射线上．已知，，则（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据，点在射线上，可求出，根据，即可求解．
【详解】解：∵，点在射线上，，
∴，
∵，，
∴，
故选：．
【点睛】本题主要考查平行线的性质，理解并掌握平行线的性质，角度的计算方法是解题的关键．
9. 已知：平行四边形的顶点，点在轴的正半轴上，按以下步骤作图：
①以点为圆心，适当长为半径画弧，分别交于点，交于点．
②分别以点，为圆心，大于的长为半径画弧，两弧在内相交于点
③画射线，交于点，则点的坐标为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了作图复杂作图．也考查了坐标与图形性质和平行四边形性质．交轴于点，如图，利用基本作图得到，再根据平行四边形的性质和平行线的性质得到，所以，设，则，，在中利用勾股定理得到，然后解方程求出，从而得到点坐标．
【详解】解：交轴于点，如图，
由作法得平分，
，
四边形为平行四边形，
∴，
，
，
设，则，
，
，，
，
，
在中，，
解得，
点坐标为．
故选：A．
10. 已知一次函数y=kx+3（k≠0）的图象经过点A，且函数值y随x的增大而增大，则点A的坐标可能是（ ）
A. （﹣2，﹣4）B. （1，2）C. （﹣2，4）D. （2，﹣1）
【答案】A
【解析】
【分析】先根据一次函数的增减性判断出k的符号，再对各选项进行逐一分析即可．
【详解】∵一次函数y=kx+2(k≠0)的函数值y随x的增大而增大，
∴k>0.
A. ∵当x=-2，y=-4时，-2k+3=-4，解得k=3.5>0，∴此点符合题意，故本选项正确；
B ∵当x=1，y=2时， k+3=2，解得k=-1<0，∴此点不符合题意，故本选项错误；
C. ∵当x=-2，y=4时，-2k+3=4，解得k=−0.5<0，∴此点不符合题意，故本选项错误；
D. ∵当x=2，y=−1时，2k+3=−1，解得k=-2<0，∴此点不符合题意，故本选项错误.
故答案选A.
.
【点睛】本题考查的知识点是一次函数图像上点的坐标特征，解题的关键是熟练的掌握一次函数图像上点的坐标特征.
二．填空题（共5小题，每题3分，共15分）
11. 要使式子在实数范围内有意义，则实数a的取值范围是______________．
【答案】且
【解析】
【分析】本题考查了二次根式有意义的条件，分式有意义的条件．根据被开方数大于等于0，分母不等于0列式计算即可得解．
详解】解：由题意得，且，
解得且．
故答案为：且．
12. 如图，在平面直角坐标中，正方形与正方形是以点为位似中心的位似图形，且相似比为，两个正方形在原点同侧，点、、在轴上，其余顶点在第一象限，若正方形的边长为，则点的坐标为______．
【答案】
【解析】
【分析】直接利用位似图形的性质结合相似比得出的长，进而得出的长，即可得出答案．
【详解】解：正方形与正方形是以原点为位似中心的位似图形，且相似比为，
，
，
，
∴，
∴，
解得：，
，
点坐标：，
故答案为：．
【点睛】此题主要考查了图形的位似变换，根据题意正确得出的长是解题关键．
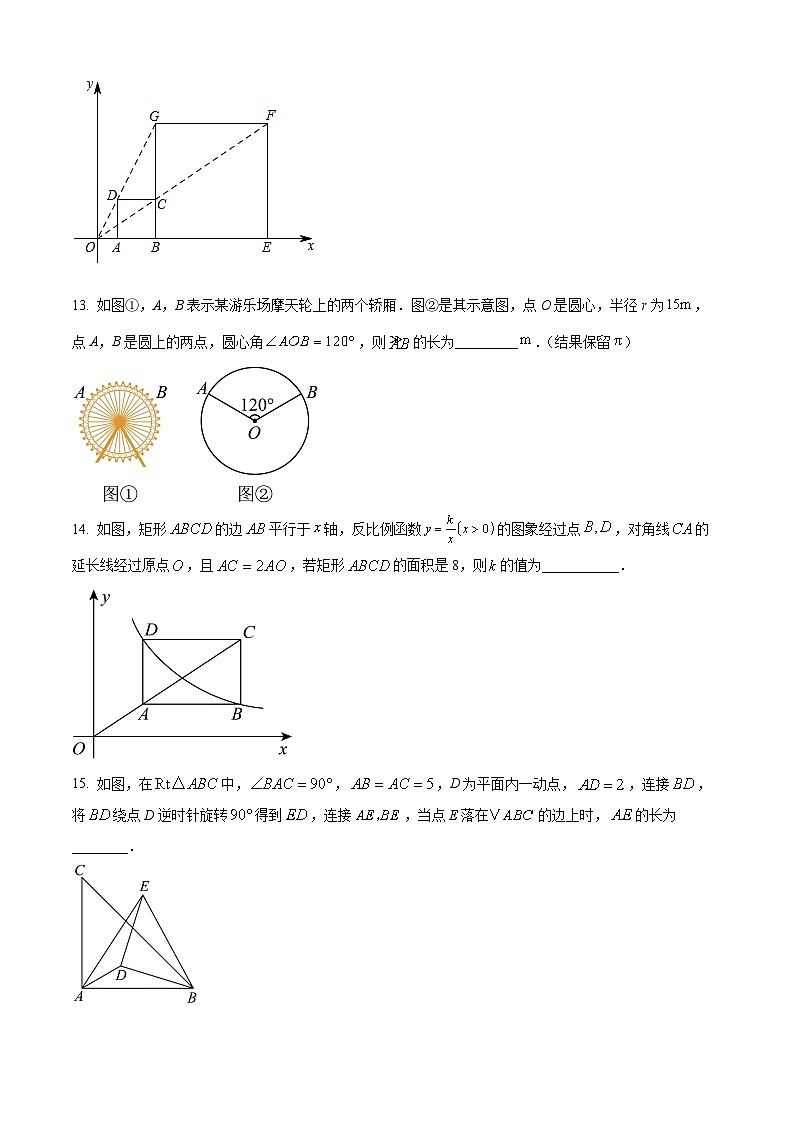
13. 如图①，A，B表示某游乐场摩天轮上的两个轿厢．图②是其示意图，点O是圆心，半径r为，点A，B是圆上的两点，圆心角，则的长为_________．（结果保留）

【答案】
【解析】
【分析】利用弧长公式直接计算即可．
【详解】∵半径，圆心角，
∴，
故答案为：．
【点睛】本题考查了弧长计算，熟练掌握弧长公式，并规范计算是解题的关键．
14. 如图，矩形的边平行于轴，反比例函数的图象经过点，对角线的延长线经过原点，且，若矩形的面积是8，则的值为___________．

【答案】6
【解析】
【分析】延长交x轴于点F，设，利用相似三角形的判定与性质可求得矩形的长与宽，再由矩形的面积即可求和k的值．
【详解】解：延长交x轴于点F，如图，
由点D在反比例函数的图象上，则设，
∵矩形的边平行于轴，，，
∴轴，，
则，
∵，
∴，
∴，
∵，
∴，
∴，，
∵，即，
∴，
故答案为：6．
【点睛】本题考查了相似三角形的判定与性质，反比例函数图象上点的坐标特征，其中相似三角形的判定与性质是关键．
15. 如图，在中，，，D为平面内一动点，，连接，将绕点D逆时针旋转得到，连接，当点E落在的边上时，的长为________．
【答案】或
【解析】
【分析】首先得到，均为等腰直角三角形，然后根据题意分两种情况讨论，点E落在边上和点E落在边上，然后分别根据勾股定理和相似三角形的性质求解即可．
【详解】∵在中，，，
∴为等腰直角三角形，
∵将绕点D逆时针旋转得到，
∴均为等腰直角三角形，
∴，
①当点E落在边上时，如图所示，则点D在边上，
∴，
在中，；
②当点E落在边上时，如解图2所示．
∵，
∴，
∵，
∴，
∴，
∴，
∴．
综上所述，的长为或．
【点睛】此题考查了旋转的性质，等腰直角三角形的判定与性质，相似三角形的判定与性质，解题的关键是根据题意分情况讨论．
三．解答题（共8小题，共75分）
16. （1）计算：
（2）先化简，再求值：，其中.
【答案】(1) ；（2），原式.
【解析】
【分析】(1)先计算三角函数值，零次幂和负整数指数幂，再进行实数的混合运算，即可；
(2)根据分式的混合运算法则，先化简，再代入求值，即可
【详解】(1)原式
；
（2）原式
当时，原式
【点睛】本题主要考查实数的混合运算法则和分式的混合运算法则，掌握分式的通分和约分是解题的关键.
17. 某商店购进甲、乙两种商品，已知每件甲种商品的价格比每件乙种商品的价格贵8元，用2400元购买甲种商品的件数恰好与用2000元购买乙种商品的件数相同．
（1）求甲、乙两种商品每件的价格各是多少元？
（2）计划购买这两种商品共80件，且投入的经费不超过3600元，那么最多可购买多少件甲种商品？
【答案】（1）每件甲种商品的价格为48元，每件乙种商品的价格为40元
（2）最多可购买50件甲种商品
【解析】
【分析】（1）设每件乙种商品的价格为元，每件甲种商品的价格为元，根据题意列出分式方程，解方程即可求解；
（2）设购买件甲种商品，则购买件乙种商品，根据题意，列出一元一次不等式，解不等式即可求解．
【小问1详解】
设每件乙种商品的价格为元，每件甲种商品的价格为元，
依题意得：，
解得：，
经检验，是原方程的解，且符合题意，
∴．
答：每件甲种商品的价格为元，每件乙种商品的价格为元．
【小问2详解】
设购买件甲种商品，则购买件乙种商品，
依题意得：，
解得：，
∴m的最大值为50．
答：最多可购买50件甲种商品．
【点睛】本题考查了分式方程的应用，一元一次不等式的应用，根据题意列出方程与不等式是解题的关键．
18. 2022年3月25日，教育部印发《义务教育课程方案和课程标准（2022年版）》，优化了课程设置，将劳动从综合实践活动课程中独立出来．某校以中国传统节日端午节为契机，组织全体学生参加包粽子劳动体验活动，随机调查了部分学生，对他们每个人平均包一个粽子的时长进行统计，并根据统计结果绘制成如下不完整的统计图表．
根据图表信息，解答下列问题：
（1）本次调查的学生总人数为 ，表中x的值为 ；
（2）该校共有500名学生，请你估计等级为B的学生人数；
（3）本次调查中，等级为A的4人中有两名男生和两名女生，若从中随机抽取两人进行活动感想交流，请利用画树状图或列表的方法，求恰好抽到一名男生和一名女生的概率．
【答案】（1）50人，
（2）200人 （3）
【解析】
【分析】本题考查的是用列表法或画树状图法求概率，用样本估计总体，条形统计图，用列表法或画树状图法不重复不遗漏的列出所有可能的结果是解题的关键．
（1）用D等级人数除以它所占的百分比得到调查的总人数，然后用4除以总人数得到x的值；
（2）用500乘以B等级人数所占的百分比即可；
（3）列表法展示所有12种等可能的结果，找出一名男生和一名女生的结果数，然后根据概率公式求解．
【小问1详解】
解：∵D组人数为 8 人，所占百分比为，
∴总人数为（人），
∴．
【小问2详解】
解：等级为B的学生所占的百分比为，
∴等级为B的学生人数为（人）．
【小问3详解】
解：记两名男生为a，b，记两名女生为c，d，列出表格如下：
∴一共有 12 种情况，其中恰有一男一女的有 8 种，
∴恰好抽到一名男生和一名女生的概率．
19. 小李、小王分别从甲地出发，骑自行车沿同一条路到乙地参加公益活动．如图，折线和线段CD分别表示小李、小王离甲地的距离y（单位：千米）与时间x（单位：小时）之间的函数关系．根据图中提供的信息，解答下列问题：
（1）求小王的骑车速度，点C的横坐标；
（2）求线段AB对应的函数表达式；
（3）当小王到达乙地时，小李距乙地还有多远？
【答案】（1）18千米/小时，
（2）； （3）4.5千米
【解析】
【分析】（1）根据函数图象中的数据先求出小王的骑车速度，再求出点C的坐标；
（2）用待定系数法可以求得线段AB对应的函数表达式；
（3）将x=2代入（2）中的函数解析式求出相应的y的值，再用减去此时的y值即可求得当小王到达乙地时，小李距乙地的距离．
【小问1详解】
解：由图可得，
小王的骑车速度是：(千米/小时)，
点C的横坐标为：；
【小问2详解】
设线段AB对应的函数表达式为，
∵，，
∴，
解得：，
∴线段AB对应的函数表达式为；
【小问3详解】
当时，，
∴此时小李距离乙地的距离为：（千米），
答：当小王到达乙地时，小李距乙地还有千米．
【点睛】本题考查了从函数图象获取信息，以及一次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
20. 2022年2月20日，举世瞩目的北京冬奥会圆满落下帷幕．本次冬奥会的成功举办掀起了全民冰雪运动的热潮．图1、图2分别是一名滑雪运动员在滑雪过程中某一时刻的实物图与示意图，已知运动员的小腿与斜坡垂直，大腿与斜坡平行，G为头部，假设G，E，D三点共线且头部到斜坡的距离为，上身与大腿夹角，膝盖与滑雪板后端的距离长为，．
（1）求此滑雪运动员的小腿的长度；
（2）求此运动员的身高．（参考数据：，，）
【答案】（1）
（2）
【解析】
【分析】本题考查解直角三角形的应用—坡度坡角问题，掌握锐角三角函数的定义是解答本题的关键．
（1）根据含30度角直角三角形的特征即可得出．
（2）由（1）得，，则，再得出，，最后根据运动员的身高为即可解答．
【小问1详解】
解：在中，，
∴，
∴此滑雪运动员的小腿的长度为．
【小问2详解】
解：由（1）得，，
∴，
∵，
∴，
在中，，，
∴，
∴运动员的身高为．
21. 如图，是的直径，是的切线，、是的弦，且，垂足为，连接并延长，交于点．
（1）求证：；
（2）若的半径，，求线段的长．
【答案】（1）证明见解析
（2）
【解析】
【分析】（1）根据平行线的判定和切线的性质、圆周角定理解答即可；
（2）通过添加辅助线，构造出直角三角形，利用勾股定理和相似三角形的判定和性质解答即可．
【小问1详解】
证明：是的切线，
，
，
，
，
，
，
；
【小问2详解】
解：连接，如图所示：
是直径，
，
，，
，
，
在中，，，则由勾股定理可得，
，，
，
，
，
，
．
【点睛】本题主要考查圆的综合，涉及切线的性质、平行线的判定与性质、圆周角定理、互余性质、勾股定理、相似三角形的判定和性质，熟练掌握相关几何性质定理是解题的关键．
22. 如图的题目中黑色区域是被污染后留下的痕迹，上面的文字已经无法辨认，导致题目中缺少一个条件而无法解答，经查询发现，该二次函数的解析式为．
已知二次函数的图像经过点和点B与y轴交于点C，求抛物线的解析式．

（1）请根据已有的信息添上这个条件是________；
（2）当时，函数的最大值是________，最小值是________；
（3）若点D为抛物线上任意一点，连接．
①当时，求直线的解析式；
②若将抛物线向下平移3个单位得到新抛物线，其中平移后的点D对应点E．当时，求点D的坐标．
【答案】（1）
（2），
（3）①，②或
【解析】
【分析】（1）先解，得 ，得，即可得答案；
（2）先求出抛物线的顶点坐标，根据二次函数的性质及，即可求答案；
（3）①过点C作的垂线交的延长线于点E，过点E作轴于点F，先求出，求出点和，再设直线的解析式为，将将和坐标代入，计算即可得答案；②连接交x轴与点F，设点，求出，再先求出，得，解得，，即可得答案．
【小问1详解】
解：
解得：，
，
添上这个条件是；
【小问2详解】
，
抛物线的顶点坐标是，
，
函数的最大值是，
，
函数的最小值是，
函数的最大值是，最小值是；
【小问3详解】
①如图，过点C作的垂线交的延长线于点E，过点E作轴于点F，

，
，
，
是等腰直角三角形，
，
轴，
，
，
又，
，
，
，
，
，
，
，
，
设直线的解析式为，
将和坐标代入，
解得：，
直线的解析式；
②如图，连接交x轴与点F，设点，

过点E的抛物线是由过点D的抛物线向下平移3个单位长得到的，
平移后的抛物线为，且轴，，
则，，，
，
，
，
，而，
，
，
，
解得，，
当时，，
当时，，
点D的坐标为或．
【点睛】本题考查了二次函数的图像和性质，三角形全等判定和性质，三角形相似的判定与性质，解题的关键是掌握二次函数的图像和性质，二次函数的平移性质，数形结合做题．
23. 某数学课外活动小组在学习了勾股定理之后，针对图1中所示的“由直角三角形三边向外侧作多边形，它们的面积之间的关系问题”进行了以下探究：
类比探究：
（1）如图2，在中，为斜边，分别以为直径，向外侧作半圆，则面积之间的关系式为_____________；
推广验证：
（2）如图3，在中，为斜边，分别以为边向外侧作，，满足，则（1）中所得关系式是否仍然成立？若成立，请证明你的结论；若不成立，请说明理由；
拓展应用：
（3）如图4，在五边形中，，点在上，，求五边形的面积．
【答案】（1）S1+S2=S3，(2)成立，证明见解析，（3）
【解析】
【分析】（1）分别写出三个半圆的面积，再利用勾股定理转化即可．
（2）先证明三个三角形相似，再计算出三个三角形的面积，即可得出结论．
（3）先添加辅助线，在第二问的思路下，先证明三个三角形相似，得出三个三角形的面积关系，再利用30°、45°的直角三角形计算出相应的边，计算出五边形的面积即可．
【详解】解：（1）设AB=b,AC=a,BC=c.则有：
所以
在Rt△ABC中，有a2+b2=c2，且
故答案为：S1+S2=S3
（2）∵
∴
设AB、AC、BC边上的高分别为h1，h2，h3
∴，设AB=b,AC=a,BC=c
则
∴

又在Rt△ABC中，有a2+b2=c2
∴
故依然成立
（3）连接PD、BD，作AF⊥BP，EM⊥PD
∵∠ABP=30°，∠BAP=105°
∴∠APB=45°
在Rt△ABF中，AF= AB= , BF=3,在Rt△AFP中,AF=PF=,则AP= ，
∵∠A=∠E,
∴△ABP∽△EDP
∴∠EPD=45°∠EDP=30°
∴∠BPD=90° 又PE=
∴PM=EM=1,MD=
则PD=1+
∴


=

所以五边形的面积为：
【点睛】本题考查勾股定理、与勾股定理有关的图形问题、相似三角形．是中考的常考知识．
等级
实践t（单位：分钟）
人数
所占百分比
A
4
x
B
20
C
D
a
b
c
d
a
b
c
d