



还剩21页未读,
继续阅读
成套系列资料,整套一键下载
青岛版数学五上 回顾整理-总复习2 图形与几何 统计与概率 课件
展开
这是一份青岛版数学五上 回顾整理-总复习2 图形与几何 统计与概率 课件,共29页。
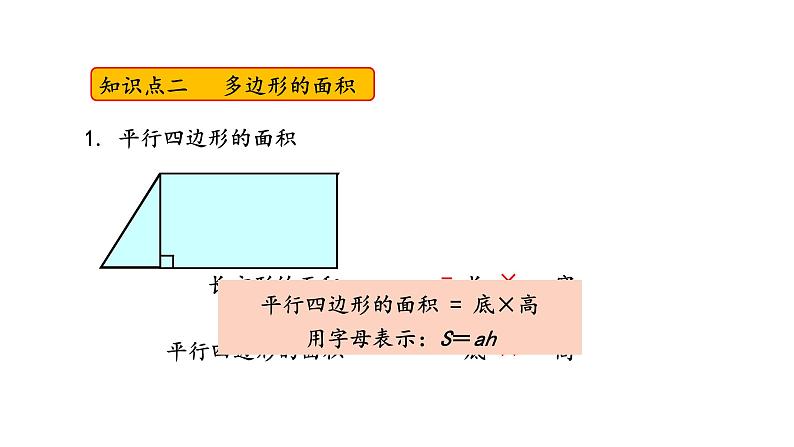
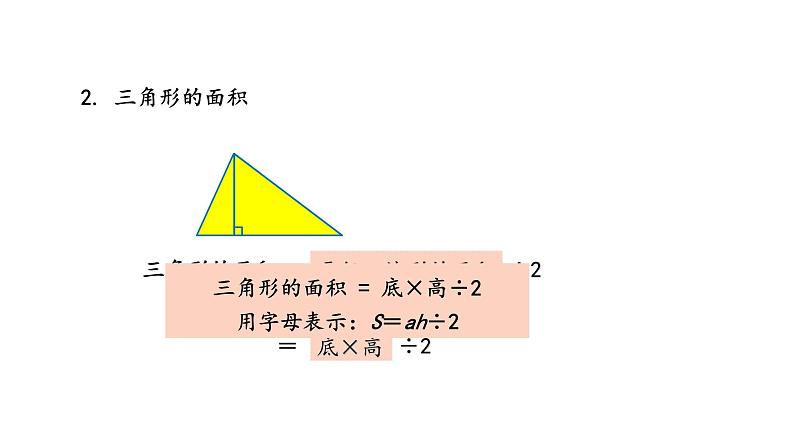
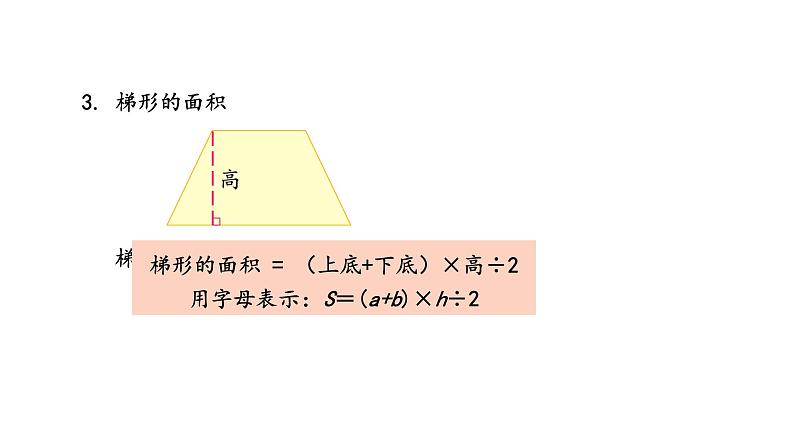
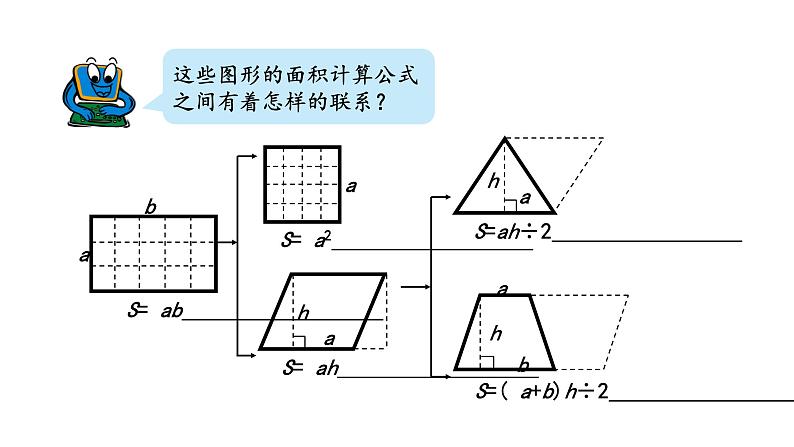
回顾整理——总复习第2课时 图形与几何知识点一 对称、平移与旋转1.轴对称图形和对称轴 将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,这样的图形叫做轴对称图形。对称轴2. 平移先画出平移的基本图形确定平移的方向确定平移的距离 物体或图形平移后,它们的大小、形状、方向都不改变,只是位置发生了变化。3. 旋转O图形旋转的三个要素:旋转中心、旋转方向和旋转角度物体或图形旋转后,形状、大小不变,只是位置和方向改变了。知识点二 多边形的面积1. 平行四边形的面积= ×= ×平行四边形的面积 = 底×高用字母表示:S=ah2. 三角形的面积三角形的面积=平行四边形的面积÷2底×高=÷2三角形的面积 = 底×高÷2用字母表示:S=ah÷23. 梯形的面积梯形的面积 = 平行四边形的面积÷2=(上底+下底)×高÷2梯形的面积 = (上底+下底)×高÷2用字母表示:S=(a+b)×h÷2这些图形的面积计算公式之间有着怎样的联系?4. 组合的面积分割法:将组合图形分割成两个或两个以上的基本图形的方法。添补法:通过添加辅助线,将组合图形转化成基本图形的方法。转化成基本图形新图形学过的图形割、补、拼转 化5. 常用的面积单位及进率平方厘米平方分米平方米公顷平方千米 100 100 10000 100随堂小练1. 计算下面各图形的面积。(单位:厘米)(教材P118页 第15题)2.2×4÷2= 4.4(cm2)3.8×7= 26.6(cm2)(20+60)×20÷2= 800(cm2)随堂小练S组合图形 = S长方形 + S三角形 三角形的面积:20×50÷2 = 500 (cm²)长方形的面积:50×65 = 3250 (cm²)总面积:500+3250 = 3750 (cm²)随堂小练2. 哪种说法正确?(单位:分米)(教材P118页 第16题)A. 三角形的面积最大 B. 梯形的面积最大C. 平行四边形的面积最大 D. 三种图形的面积一样大√随堂小练3.(教材P119页 第17题) (1)我国陆地面积约 960 万( )。 A.平方米 B.公顷 C.平方千米(2)实验小学占地约 2( )。 A.平方千米 B.公顷 C.平方米(3)足球场占地面积约 7140( )。 A.平方千米 B.公顷 C.平方米CBC随堂小练4. 右图是一个樱桃园,平均每棵樱桃树占地 9 平方米。园中大约可种多少棵樱桃树?(教材P119页 第18题)[(25+35)×21÷2] ÷9= 70(棵)答:这块地大约可种 70 棵樱桃树。随堂小练5.按要求画图。(教材P119页 第19题)(1)画出左图的另一半,使它成为一个轴对称图形。(2)将右图绕O点顺时针旋转90°,再向左平移3格。随堂小练5.按要求画图。(教材P119页 第19题)(2)将右图绕O点顺时针旋转90°,再向左平移3格。学习完本节课,你有什么收获?课堂小结1.从课后习题中选取;2.完成练习册本课时的习题。课后作业回顾整理——总复习第3课时 统计与概率折线统计图的特点及绘制1.折线统计图折线统计图不仅可以反映数量的多少,还可以清楚地反映数量的增减变化情况。用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来。2. 绘制折线统计图的一般步骤(1)写出统计图的标题和制图日期;(2)根据图纸的大小画出两条互相垂直的射线,并根据题意标出每条线表示的量及其单位;(3)在水平射线(即横轴)上适当分配各点的位置,确定各点间隔,并标出相应的数据;(4)在与水平射线垂直的射线(即纵轴)上,根据数据大小的具体情况,确定单位长度; (5)按照数据的大小描出各点,再用线段依次连接各点。3. 选择合适的统计图如果只需要反映数量的多少,那么选用条形统计图;如果既要反映数量的多少, 又要反映数量的增减变化情况, 那么选用折线统计图。要表示某地区去年一年降水量的变化情况,应该选用( )统计图。要表示某商店一个季度中每月销售铅笔数量的多少,应该选用( )统计图。条形折线随堂小练1. 有人对记忆外语单词情况进行测试,得到了这样一组数据。(教材P121页 第4题)随堂小练选择合适的统计图表示上面的数据。分析统计图,你能发现什么?选择折线统计图表示数据。100292015131212根据统计数据可以看出,第一天忘记的单词数量最多,第二天忘记的单词数量大幅度减少,第三天后记住的单词个数基本确定。随堂小练2. 立夏是夏季的第一个节气,很多人认为立夏就是夏天了,其实不然,在气象学上入夏的标准:首次出现连续 5 天日平均气温大于或等于22 ℃,那么这 5 天的首日即入夏日。下面是 2022 年 5 月 18 日-5 月 27 日某市日平均气温变化情况统计图。随堂小练(1)在此期间,日平均气温最高是 5 月( )日和 5 月( )日,最低是 5 月( )日。(2)已知该市近 30 年平均入夏日为 5 月 19 日,2020 年 5 月 18 日之前没有连续 5 天日平均气温大于或等于 22 ℃。 根据上面统计图可以看出,从 5 月( )日到 5 月( )日这 5 天该市日平均气温首次连续大于或等于 22℃, 由此确定该市 2022 年入夏的时间是5 月( )日。(3)从入夏起的连续 5 天的平均气温是多少?22.6+24.9+27.6+27.3+27.6)÷5=26(℃)答:从入夏起的连续 5 天的平均气温是 26 ℃。23251921 2521 学习完本节课,你有什么收获?课堂小结1.从课后习题中选取;2.完成练习册本课时的习题。课后作业
回顾整理——总复习第2课时 图形与几何知识点一 对称、平移与旋转1.轴对称图形和对称轴 将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,这样的图形叫做轴对称图形。对称轴2. 平移先画出平移的基本图形确定平移的方向确定平移的距离 物体或图形平移后,它们的大小、形状、方向都不改变,只是位置发生了变化。3. 旋转O图形旋转的三个要素:旋转中心、旋转方向和旋转角度物体或图形旋转后,形状、大小不变,只是位置和方向改变了。知识点二 多边形的面积1. 平行四边形的面积= ×= ×平行四边形的面积 = 底×高用字母表示:S=ah2. 三角形的面积三角形的面积=平行四边形的面积÷2底×高=÷2三角形的面积 = 底×高÷2用字母表示:S=ah÷23. 梯形的面积梯形的面积 = 平行四边形的面积÷2=(上底+下底)×高÷2梯形的面积 = (上底+下底)×高÷2用字母表示:S=(a+b)×h÷2这些图形的面积计算公式之间有着怎样的联系?4. 组合的面积分割法:将组合图形分割成两个或两个以上的基本图形的方法。添补法:通过添加辅助线,将组合图形转化成基本图形的方法。转化成基本图形新图形学过的图形割、补、拼转 化5. 常用的面积单位及进率平方厘米平方分米平方米公顷平方千米 100 100 10000 100随堂小练1. 计算下面各图形的面积。(单位:厘米)(教材P118页 第15题)2.2×4÷2= 4.4(cm2)3.8×7= 26.6(cm2)(20+60)×20÷2= 800(cm2)随堂小练S组合图形 = S长方形 + S三角形 三角形的面积:20×50÷2 = 500 (cm²)长方形的面积:50×65 = 3250 (cm²)总面积:500+3250 = 3750 (cm²)随堂小练2. 哪种说法正确?(单位:分米)(教材P118页 第16题)A. 三角形的面积最大 B. 梯形的面积最大C. 平行四边形的面积最大 D. 三种图形的面积一样大√随堂小练3.(教材P119页 第17题) (1)我国陆地面积约 960 万( )。 A.平方米 B.公顷 C.平方千米(2)实验小学占地约 2( )。 A.平方千米 B.公顷 C.平方米(3)足球场占地面积约 7140( )。 A.平方千米 B.公顷 C.平方米CBC随堂小练4. 右图是一个樱桃园,平均每棵樱桃树占地 9 平方米。园中大约可种多少棵樱桃树?(教材P119页 第18题)[(25+35)×21÷2] ÷9= 70(棵)答:这块地大约可种 70 棵樱桃树。随堂小练5.按要求画图。(教材P119页 第19题)(1)画出左图的另一半,使它成为一个轴对称图形。(2)将右图绕O点顺时针旋转90°,再向左平移3格。随堂小练5.按要求画图。(教材P119页 第19题)(2)将右图绕O点顺时针旋转90°,再向左平移3格。学习完本节课,你有什么收获?课堂小结1.从课后习题中选取;2.完成练习册本课时的习题。课后作业回顾整理——总复习第3课时 统计与概率折线统计图的特点及绘制1.折线统计图折线统计图不仅可以反映数量的多少,还可以清楚地反映数量的增减变化情况。用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来。2. 绘制折线统计图的一般步骤(1)写出统计图的标题和制图日期;(2)根据图纸的大小画出两条互相垂直的射线,并根据题意标出每条线表示的量及其单位;(3)在水平射线(即横轴)上适当分配各点的位置,确定各点间隔,并标出相应的数据;(4)在与水平射线垂直的射线(即纵轴)上,根据数据大小的具体情况,确定单位长度; (5)按照数据的大小描出各点,再用线段依次连接各点。3. 选择合适的统计图如果只需要反映数量的多少,那么选用条形统计图;如果既要反映数量的多少, 又要反映数量的增减变化情况, 那么选用折线统计图。要表示某地区去年一年降水量的变化情况,应该选用( )统计图。要表示某商店一个季度中每月销售铅笔数量的多少,应该选用( )统计图。条形折线随堂小练1. 有人对记忆外语单词情况进行测试,得到了这样一组数据。(教材P121页 第4题)随堂小练选择合适的统计图表示上面的数据。分析统计图,你能发现什么?选择折线统计图表示数据。100292015131212根据统计数据可以看出,第一天忘记的单词数量最多,第二天忘记的单词数量大幅度减少,第三天后记住的单词个数基本确定。随堂小练2. 立夏是夏季的第一个节气,很多人认为立夏就是夏天了,其实不然,在气象学上入夏的标准:首次出现连续 5 天日平均气温大于或等于22 ℃,那么这 5 天的首日即入夏日。下面是 2022 年 5 月 18 日-5 月 27 日某市日平均气温变化情况统计图。随堂小练(1)在此期间,日平均气温最高是 5 月( )日和 5 月( )日,最低是 5 月( )日。(2)已知该市近 30 年平均入夏日为 5 月 19 日,2020 年 5 月 18 日之前没有连续 5 天日平均气温大于或等于 22 ℃。 根据上面统计图可以看出,从 5 月( )日到 5 月( )日这 5 天该市日平均气温首次连续大于或等于 22℃, 由此确定该市 2022 年入夏的时间是5 月( )日。(3)从入夏起的连续 5 天的平均气温是多少?22.6+24.9+27.6+27.3+27.6)÷5=26(℃)答:从入夏起的连续 5 天的平均气温是 26 ℃。23251921 2521 学习完本节课,你有什么收获?课堂小结1.从课后习题中选取;2.完成练习册本课时的习题。课后作业











