




中职高教版(2021·十四五)5.1.2 复数的几何意义完整版ppt课件
展开5.1.2复数的几何意义
例如,复平面内的原点O(0,0)表示实数O,点A(1,0)表示实数,点B(0,-1)表示纯虚数-i,点D(1,-1 )表示复数 1- i.
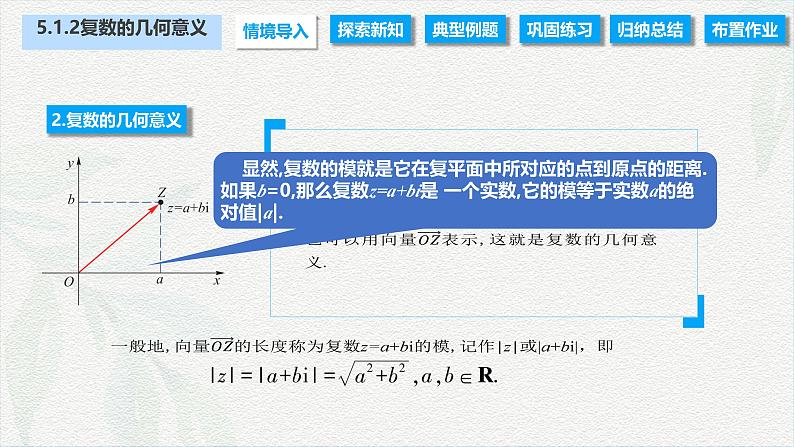
显然,复数的模就是它在复平面中所对应的点到原点的距离.如果b=0,那么复数z=a+bi是 一个实数,它的模等于实数a的绝对值|a|.
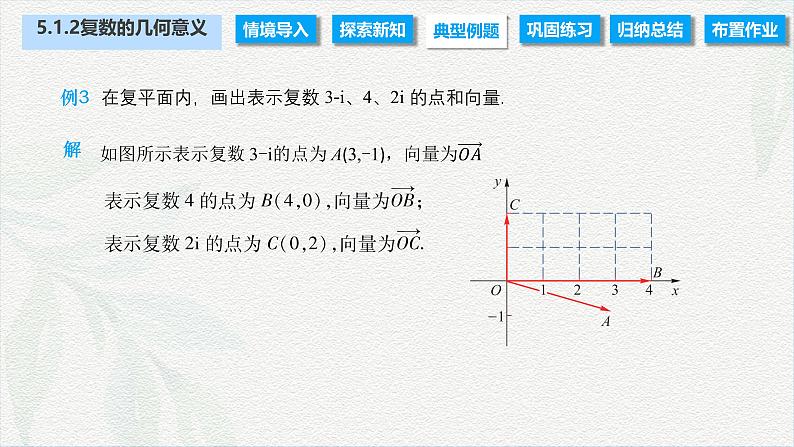
例3 在复平面内,画出表示复数 3-i、4、2i 的点和向量.
设复数z在复平面内对应的点为 Z,问满足下列条件的点Z的集合是什么图形?(1)|z|=3;(2)2≤|z|≤3.
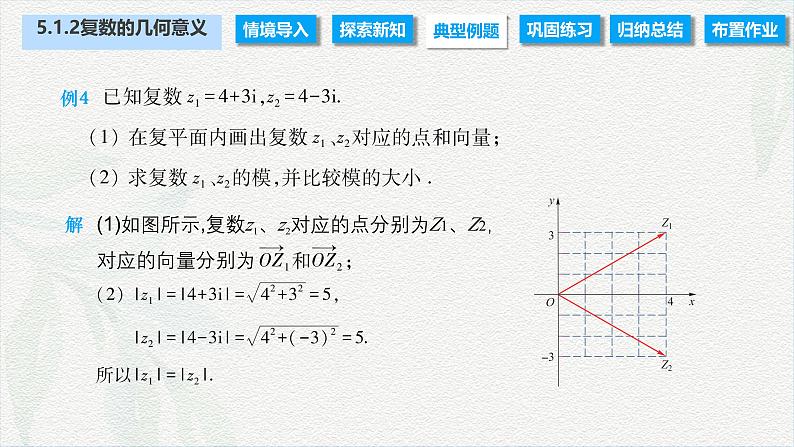
两个实数可以比较大小,试问两个复数可以比较大小吗?
作 业
1.书面作业:完成教材第165页习题5.1;2.查漏补缺:根据个人情况对课堂学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.
数学拓展模块一(上册)4.2.1 共面直线一等奖ppt课件: 这是一份数学拓展模块一(上册)<a href="/sx/tb_c4053649_t3/?tag_id=26" target="_blank">4.2.1 共面直线一等奖ppt课件</a>,共17页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,21共面直线,情境导入,异面直线,平行直线,相交直线等内容,欢迎下载使用。
中职数学高教版(2021·十四五)拓展模块一(上册)2.3 向量的内积获奖ppt课件: 这是一份中职数学高教版(2021·十四五)拓展模块一(上册)<a href="/sx/tb_c4053622_t3/?tag_id=26" target="_blank">2.3 向量的内积获奖ppt课件</a>,共15页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,3向量的内积,情境导入,向量的夹角,练一练,向量的内积等内容,欢迎下载使用。
中职数学第2章 平面向量2.2 向量的线性运算2.2.2 向量的减法运算优质课ppt课件: 这是一份中职数学<a href="/sx/tb_c4053619_t3/?tag_id=26" target="_blank">第2章 平面向量2.2 向量的线性运算2.2.2 向量的减法运算优质课ppt课件</a>,共11页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,情境导入,②连接两向量终点,简记口诀等内容,欢迎下载使用。












