



中职高教版(2021·十四五)2.2.1 向量的加法运算优秀课件ppt
展开2.2.1向量的加法运算
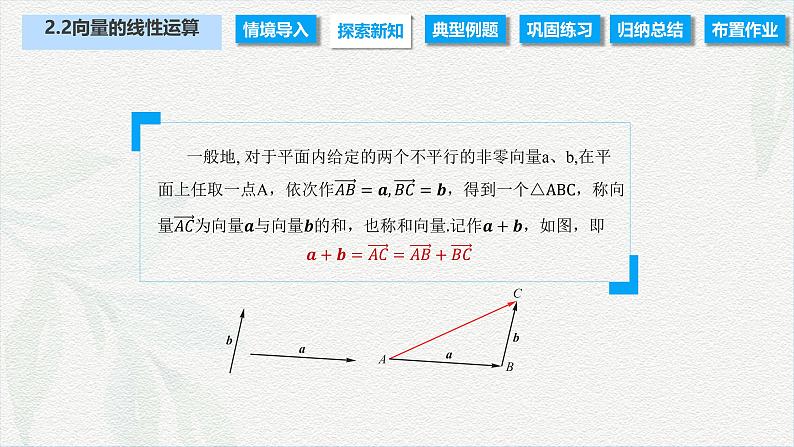
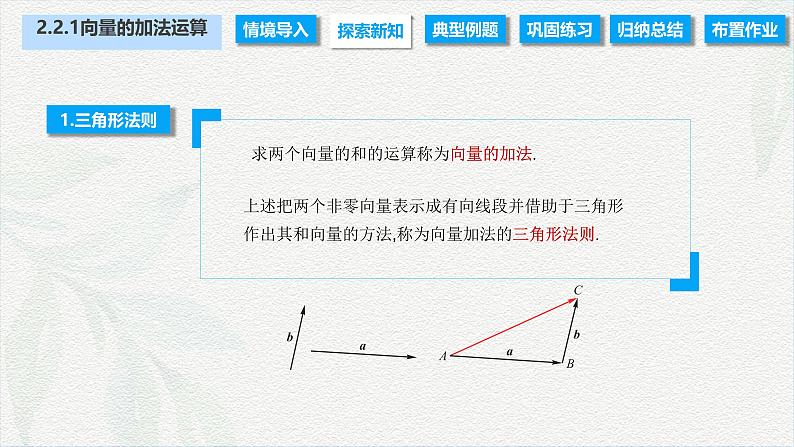
上述把两个非零向量表示成有向线段并借助于三角形作出其和向量的方法,称为向量加法的三角形法则.
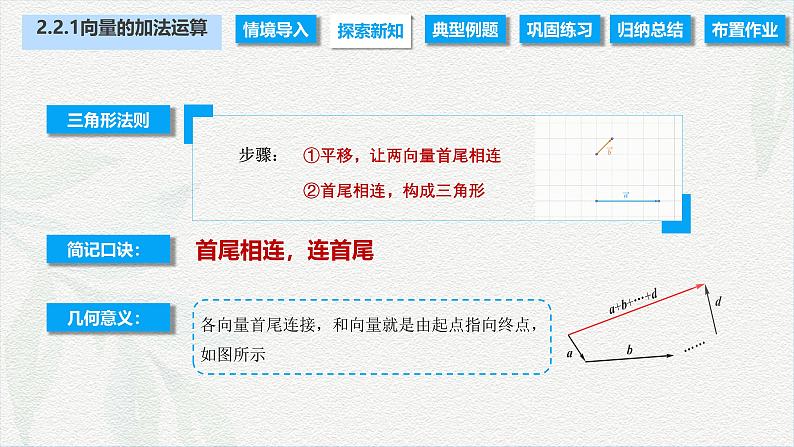
①平移,让两向量首尾相连
②首尾相连,构成三角形
各向量首尾连接,和向量就是由起点指向终点,如图所示
①将两个向量平移至同一个起点 .
③两个向量之间的对角线即为两个向量的和 .
可以验证,向量的加法满足以下运算律
a+b=b+a;(交换律) a+(b+c)= a+(b+c) .(结合律)
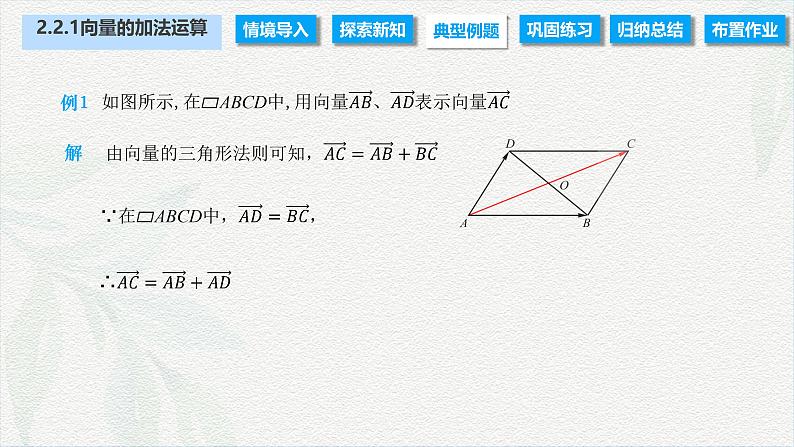
例2 已知向量a、b,如图(1)所示,试分别用向量加法的三角形法则和平行四边形法则作向量a+b.
例3 一艘渡轮要从南岸到北岸,它在静水中速度的大小为12km/h,方向正北. 若水流速度的大小为 12km/h,方向正东,求渡轮实际航行的速度.
因此, 船实际航行的速度大小是13km/h,方向为北偏东22°37’.
1.如图所示,分别求作下列情形下的向量a+b.
2.如图所示,已知向量a、b、c、d则(1)a+d=_________(2)c+b=_________
1.书面作业:完成教材第27页练习2.2.1,第2.3.4题;2.查漏补缺:根据个人情况对课堂学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.
中职数学高教版(2021·十四五)拓展模块一(上册)2.4.2 向量线性运算的坐标表示优质课课件ppt: 这是一份中职数学高教版(2021·十四五)拓展模块一(上册)<a href="/sx/tb_c4053625_t3/?tag_id=26" target="_blank">2.4.2 向量线性运算的坐标表示优质课课件ppt</a>,共14页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,向量线性运算坐标表示,情境导入,1-12等内容,欢迎下载使用。
中职数学高教版(2021·十四五)拓展模块一(上册)2.3 向量的内积获奖ppt课件: 这是一份中职数学高教版(2021·十四五)拓展模块一(上册)<a href="/sx/tb_c4053622_t3/?tag_id=26" target="_blank">2.3 向量的内积获奖ppt课件</a>,共15页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,3向量的内积,情境导入,向量的夹角,练一练,向量的内积等内容,欢迎下载使用。
中职数学高教版(2021·十四五)拓展模块一(上册)第2章 平面向量2.2 向量的线性运算2.2.3 向量的数乘运算精品课件ppt: 这是一份中职数学高教版(2021·十四五)拓展模块一(上册)<a href="/sx/tb_c4053620_t3/?tag_id=26" target="_blank">第2章 平面向量2.2 向量的线性运算2.2.3 向量的数乘运算精品课件ppt</a>,共16页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,情境导入,平面向量共线定理,例5计算等内容,欢迎下载使用。













