新高考数学一轮复习分层提升练习第05练 一元二次不等式及其应用（2份打包，原卷版+含解析）

这是一份新高考数学一轮复习分层提升练习第05练 一元二次不等式及其应用（2份打包，原卷版+含解析），文件包含新高考数学一轮复习分层提升练习第05练一元二次不等式及其应用原卷版doc、新高考数学一轮复习分层提升练习第05练一元二次不等式及其应用含解析doc等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。

一、单选题
1．（河南省部分学校大联考2022-2023学年高三下学期3月质量检测理科数学试题）已知全集 SKIPIF 1 < 0 ，集合 SKIPIF 1 < 0 ，则集合 SKIPIF 1 < 0 为（ ）
A．B．
C．D．
【答案】D
【分析】计算出 SKIPIF 1 < 0 ，从而根据交集，并集和补集概念计算出四个选项，得到正确答案.
【详解】由题意知 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
A选项， SKIPIF 1 < 0 ，A错误；
B选项， SKIPIF 1 < 0 ，B错误；
C选项， SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，C错误；
所以 SKIPIF 1 < 0 .
故选：D.
2．（江西省宜春市2023届高三一模数学（理）试题）设集合 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【分析】解一元二次不等式求集合A，解对数不等式求集合B，应用集合交运算求结果.
【详解】由 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
故选：C
3．（华大新高考联盟2023届高三下学期3月教学质量测评理科数学试题）若集合 SKIPIF 1 < 0 ，集合 SKIPIF 1 < 0 ，满足 SKIPIF 1 < 0 的实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【分析】解不等式可求得集合 SKIPIF 1 < 0 ，根据交集结果可确定集合 SKIPIF 1 < 0 ，由此可构造不等式求得结果.
【详解】由 SKIPIF 1 < 0 得： SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ；
由 SKIPIF 1 < 0 得： SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 .
故选：D.
4．设一元二次不等式 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【分析】根据 SKIPIF 1 < 0 和 SKIPIF 1 < 0 是方程 SKIPIF 1 < 0 的两个根，由韦达定理解得 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，可得结果.
【详解】由题意可知方程 SKIPIF 1 < 0 的根为 SKIPIF 1 < 0 ，
由韦达定理得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
故选：B.
5．（河北省承德市双滦区实验中学2023届高三上学期10月数学试题）已知集合 SKIPIF 1 < 0 ，集合 SKIPIF 1 < 0 ，若“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 ”的充分不必要条件，则实数 SKIPIF 1 < 0 的取值范围（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【分析】解分式不等式可求得集合 SKIPIF 1 < 0 ；根据充分不必要条件的定义可知 SKIPIF 1 < 0  SKIPIF 1 < 0 ；解一元二次不等式，分别讨论 SKIPIF 1 < 0 ， SKIPIF 1 < 0 和 SKIPIF 1 < 0 的情况，根据包含关系可求得结果.
【详解】由 SKIPIF 1 < 0 得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；
由 SKIPIF 1 < 0 得： SKIPIF 1 < 0 ；
SKIPIF 1 < 0 “ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 ”的充分不必要条件， SKIPIF 1 < 0  SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，不满足 SKIPIF 1 < 0  SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，不满足 SKIPIF 1 < 0  SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，若 SKIPIF 1 < 0  SKIPIF 1 < 0 ，则需 SKIPIF 1 < 0 ；
综上所述：实数 SKIPIF 1 < 0 的取值范围为 SKIPIF 1 < 0 .
故选：A.
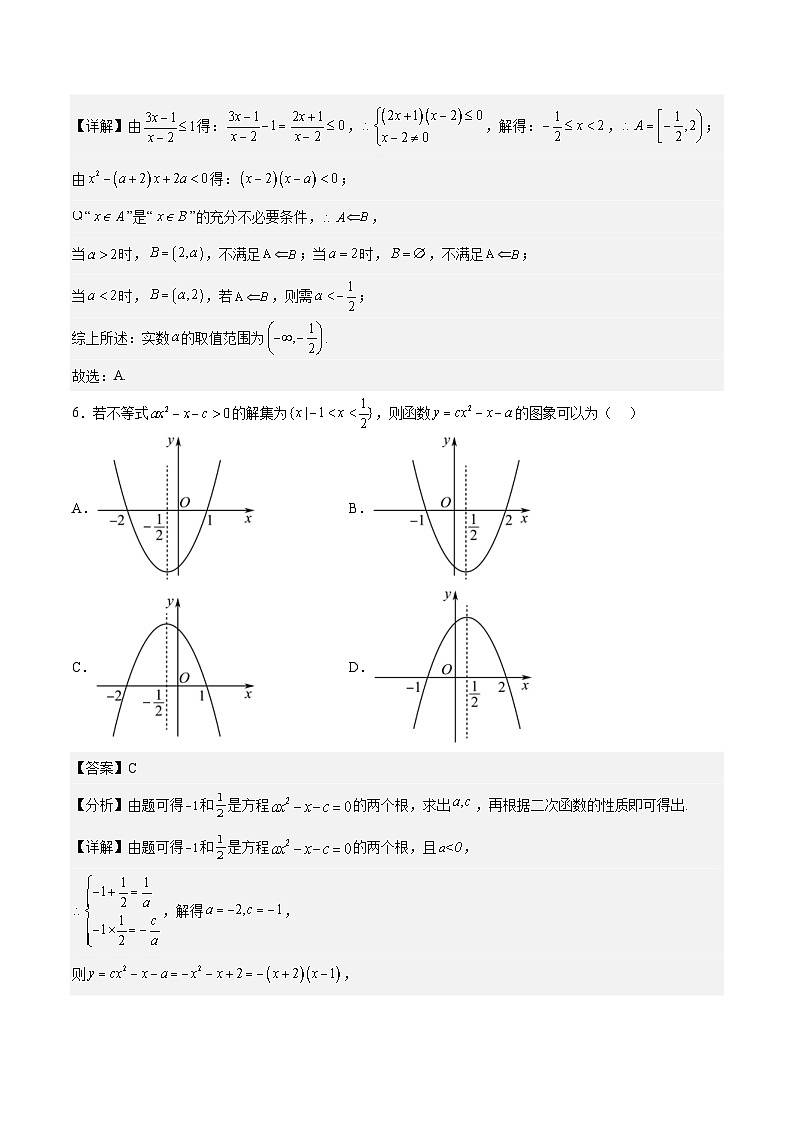
6．若不等式 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的图象可以为（ ）
A．B．
C．D．
【答案】C
【分析】由题可得 SKIPIF 1 < 0 和 SKIPIF 1 < 0 是方程 SKIPIF 1 < 0 的两个根，求出 SKIPIF 1 < 0 ，再根据二次函数的性质即可得出.
【详解】由题可得 SKIPIF 1 < 0 和 SKIPIF 1 < 0 是方程 SKIPIF 1 < 0 的两个根，且 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，
则函数图象开口向下，与 SKIPIF 1 < 0 轴交于 SKIPIF 1 < 0 .
故选：C.
二、多选题
7．已知关于x的不等式 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0
B．不等式 SKIPIF 1 < 0 的解集是 SKIPIF 1 < 0
C． SKIPIF 1 < 0
D．不等式 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0
【答案】ABD
【分析】根据不等式 SKIPIF 1 < 0 的解集判断出 SKIPIF 1 < 0 ，结合根与系数关系、一元二次不等式的解法判断BCD选项的正确性.
【详解】关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 选项正确；
且－2和3是关于 SKIPIF 1 < 0 的方程 SKIPIF 1 < 0 的两根，由韦达定理得 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，C选项错误；
不等式 SKIPIF 1 < 0 即为 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 选项正确；
不等式 SKIPIF 1 < 0 即为 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 选项正确.
故选： SKIPIF 1 < 0 .
8．已知关于 SKIPIF 1 < 0 的一元二次不等式 SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 ，则该不等式的解集可能是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】ABD
【分析】不等式变形后，确定相应二次方程的根有大小得不等式解集．
【详解】不等式变形为 SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 时，不等式解集为空集；
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
因此解集可能为ABD．
故选：ABD．
三、填空题
9．不等式 SKIPIF 1 < 0 的解集为__________________.
【答案】 SKIPIF 1 < 0
【分析】分类讨论 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，即可求出结果.
【详解】因为 SKIPIF 1 < 0 ，所以
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
所以原不等式的解集为 SKIPIF 1 < 0 .
【点睛】本题主要考查含绝对值不等式，属于基础题型.
10．不等式 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的单调递增区间是_______
【答案】 SKIPIF 1 < 0
【解析】根据不等式的解集可知一元二次不等式所对应的一元二次方程的根，利用韦达定理可求出 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的值，再根据复合函数求单调区间的方法，得出单调递增区间.
【详解】由题知-2和1是 SKIPIF 1 < 0 的两根，
由根与系数的关系知-2+1= SKIPIF 1 < 0 ，−2×1＝ SKIPIF 1 < 0 ，
由不等式的解集为 SKIPIF 1 < 0 ，可知 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，
因为函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 则该函数的增区间为 SKIPIF 1 < 0
所以 SKIPIF 1 < 0 的增区间为 SKIPIF 1 < 0
故答案为： SKIPIF 1 < 0 .
11．若关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 的解集不是空集，则 SKIPIF 1 < 0 的取值范围是________.
【答案】 SKIPIF 1 < 0 或 SKIPIF 1 < 0
【分析】分别讨论 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，利用不等式 SKIPIF 1 < 0 的解集不是空集，解出 SKIPIF 1 < 0 的取值范围.
【详解】解：若 SKIPIF 1 < 0 ，则原不等式等价为 SKIPIF 1 < 0 ，此时不等式的解集为空集，所以不成立，即 SKIPIF 1 < 0 .
若 SKIPIF 1 < 0 ，要使不等式 SKIPIF 1 < 0 的解集不是空集，
则①若 SKIPIF 1 < 0 ，有 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 .
②若 SKIPIF 1 < 0 ，则满足条件.
综上所述，满足条件的 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
【点睛】本题主要考查一元二次不等式的基本解法，属于基础题.
12．若 SKIPIF 1 < 0 和 SKIPIF 1 < 0 分别是一元二次方程 SKIPIF 1 < 0 的两根，则 SKIPIF 1 < 0 的是_____________.
【答案】 SKIPIF 1 < 0
【分析】由韦达定理得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 SKIPIF 1 < 0 ， SKIPIF 1 < 0 进而求解．
【详解】解：由韦达定理： SKIPIF 1 < 0 ， SKIPIF 1 < 0 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
【点睛】本题考查韦达定理，两根只差与两根之和、两根之积的关系．
四、解答题
13．集合 SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
(1)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求实数 SKIPIF 1 < 0 的值；
(2)从条件①②③这三个条件中选择一个作为已知条件，求实数 SKIPIF 1 < 0 的取值范围.
条件：① SKIPIF 1 < 0 ；② SKIPIF 1 < 0 ；③ SKIPIF 1 < 0 .
【答案】(1)1；
(2)条件选择见解析， SKIPIF 1 < 0 .
【分析】（1）利用元素与集合的关系，可以确定 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，求解即可；
（2）任选其中一个条件，根据集合间的关系，列式求解即可.
（1）
解：因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
且 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 得 SKIPIF 1 < 0 ；
∴实数 SKIPIF 1 < 0 的值为1.
（2）
解：集合 SKIPIF 1 < 0 .
集合 SKIPIF 1 < 0 .
若选择① SKIPIF 1 < 0 ，即 SKIPIF 1 < 0
若选择② SKIPIF 1 < 0 ，
若选择③ SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 .
14．（1）已知 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的最小值．
（2）求关于x的不等式的解集： SKIPIF 1 < 0 ．
【答案】（1）8 ；（2） SKIPIF 1 < 0 时，解集为 SKIPIF 1 < 0 ； SKIPIF 1 < 0 时，解集为 SKIPIF 1 < 0 ； SKIPIF 1 < 0 时，解集为 SKIPIF 1 < 0 ； SKIPIF 1 < 0 时，解集为 SKIPIF 1 < 0 ； SKIPIF 1 < 0 时，解集为 SKIPIF 1 < 0 ．
【分析】（1）整理可得 SKIPIF 1 < 0 ，结合基本不等式分析计算；（2）不等式分类讨论问题，结合本题，首先讨论最高项系数的符号；其次讨论两根的大小．
【详解】解：（1）因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时等号成立，
所以 SKIPIF 1 < 0 的最小值为8．
（2） SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时，不等式为 SKIPIF 1 < 0 ，解集为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 时，不等式分解因式可得 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时，故 SKIPIF 1 < 0 ，此时解集为 SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，故此时解集为 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 可化为 SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ，
解集为 SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 可化为 SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 ，解集为 SKIPIF 1 < 0 ，
综上所述： SKIPIF 1 < 0 时，解集为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 时，解集为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 时，解集为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 时，解集为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 时，解集为 SKIPIF 1 < 0 ．
【B组 在综合中考查能力】
一、单选题
1．（四川省成都市玉林中学2023届高三二诊模拟理科数学试题（三））若不等式 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有解，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【分析】由已知可得 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上有解，求出 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上的最小值，即可得出实数 SKIPIF 1 < 0 的取值范围．
【详解】因为关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上有解，
所以 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上有解，
设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上单调递减，
所以 SKIPIF 1 < 0 有最小值为 SKIPIF 1 < 0 ，
所以实数 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 ．
故选：C．
2．（2023年普通高等学校招生全国统一考试数学猜题卷（六））设函数 SKIPIF 1 < 0 ，则满足 SKIPIF 1 < 0 的整数 SKIPIF 1 < 0 的个数为（ ）
A．2B．3C．4D．5
【答案】C
【分析】首先求解关于 SKIPIF 1 < 0 的一元二次不等式，再结合函数 SKIPIF 1 < 0 的图象，求解不等式的整数解.
【详解】由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，易得当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
作出函数 SKIPIF 1 < 0 的大致图象如图所示.
故 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
结合图象，通过估算得整数解为－1，0，1，2，
故选：C.
3．（河南省平许济洛2022-2023学年高三第二次质量检测数学试题）已知命题“ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ”为真命题，则实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【分析】由题知 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，再根据二次函数求最值即可得答案.
【详解】解：因为命题“ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ”为真命题，
所以，命题“ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ”为真命题，
所以， SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
因为， SKIPIF 1 < 0 ，
所以，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，当且仅当 SKIPIF 1 < 0 时取得等号.
所以， SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，即实数 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0
故选：C
二、多选题
4．关于x的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立”的一个必要不充分条件是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】BD
【分析】求得关于x的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成时a的取值范围，根据必要不充分条件与集合包含之间的关系，即可判断答案.
【详解】由题意可知，关于x的不等式 SKIPIF 1 < 0 恒成立，
则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
对于选项A，“ SKIPIF 1 < 0 ”是“关于x的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立”的充要条件；
对于选项B， SKIPIF 1 < 0 ⫋ SKIPIF 1 < 0 ,
故“ SKIPIF 1 < 0 ”是“关于x的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立”的必要不充分条件；
对于选项C， SKIPIF 1 < 0 ⫋ SKIPIF 1 < 0 ,
“ SKIPIF 1 < 0 ”是“关于x的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立”的充分不必要条件；
对于选项D中， SKIPIF 1 < 0 ⫋ SKIPIF 1 < 0 , “ SKIPIF 1 < 0 ”是“关于x的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立”必要不充分条件，
故选：BD．
5．已知 SKIPIF 1 < 0 ，关于 SKIPIF 1 < 0 一元二次不等式 SKIPIF 1 < 0 的解集中有且仅有3个整数，则 SKIPIF 1 < 0 的值可以是（ ）
A．6B．7C．8D．9
【答案】ABC
【分析】利用对应二次函数的性质，结合题设不等式解集仅有3个整数可得 SKIPIF 1 < 0 求a的范围，即知其可能值.
【详解】由 SKIPIF 1 < 0 开口向上且对称轴为 SKIPIF 1 < 0 ，
∴要使题设不等式解集有且仅有3个整数，则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 的可能值A、B、C.符合.
故选：ABC.
三、填空题
6．（上海市宝山区2023届高三二模数学试题）已知函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 且 SKIPIF 1 < 0 ），若关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的取值范围是_________．
【答案】 SKIPIF 1 < 0
【分析】根据题意结合指数函数性质判断出 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 ，根据一元二次不等式和相应方程的关系可得 SKIPIF 1 < 0 ，结合b的范围，即可求得答案.
【详解】由题意知若 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 与 SKIPIF 1 < 0 是 SKIPIF 1 < 0 的两根，
故 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
故答案为： SKIPIF 1 < 0
7．（江苏省南通市2022-2023学年高三上学期期中数学试题）在 SKIPIF 1 < 0 中，三边长是公差为2的等差数列，若 SKIPIF 1 < 0 是钝角三角形，则其最短边长可以为______________.（写出一个满足条件的值即可）
【答案】3（答案不唯一）
【分析】设三角形的三边长为 SKIPIF 1 < 0 ，求出最短边的取值范围为 SKIPIF 1 < 0 即得解.
【详解】解：设三角形的三边长为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
因为三角形是钝角三角形，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
综合得最短边的取值范围为 SKIPIF 1 < 0 .
故答案为：3（答案不唯一）
四、解答题
8．在① SKIPIF 1 < 0 ，② SKIPIF 1 < 0 ，③ SKIPIF 1 < 0 这三个条件中任选一个，补充在下面的横线上，并回答下列问题.设全集 SKIPIF 1 < 0 ，______， SKIPIF 1 < 0
(1)若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 ；
(2)若“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 ”的充分不必要条件，求实数a的取值范围.
【答案】(1) SKIPIF 1 < 0
(2) SKIPIF 1 < 0
【分析】（1）根据除法不等式，绝对值不等式，对数函数的定义域即可分别求出三种情形下的集合A；（2）对集合B中不等式进行因式分解，再根据充分必要条件和集合包含关系即可求解.
【详解】（1）若选①：
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
故 SKIPIF 1 < 0 SKIPIF 1 < 0 .
若选②：
SKIPIF 1 < 0
SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
故 SKIPIF 1 < 0 SKIPIF 1 < 0 .
若选③：
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
故 SKIPIF 1 < 0 SKIPIF 1 < 0 .
（2）由（1）知 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
因为“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 ”的充分不必要条件，
（i）若 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
此时 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0
等号不同时取得，
解得 SKIPIF 1 < 0 .
故 SKIPIF 1 < 0 .
（ii）若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，不合题意舍去；
（iii）若 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
此时 SKIPIF 1 < 0 ，
SKIPIF 1 < 0
等号不同时取得，
解得 SKIPIF 1 < 0 .
综上所述，a的取值范围是 SKIPIF 1 < 0 .
【C组 在创新中考查思维】
一、单选题
1．（天津市南开中学2022届高三下学期高考前热身练习数学试题）已知函数 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 恰有两个零点，则实数 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【分析】函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 均有有两个零点，分类讨论每部分的零点个数，结合零点分布处理．
【详解】∵ SKIPIF 1 < 0 ，则二次函数 SKIPIF 1 < 0 有两个零点
若 SKIPIF 1 < 0 恰有两个零点，则 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0
此时 SKIPIF 1 < 0 无零点，则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0
则 SKIPIF 1 < 0
若 SKIPIF 1 < 0 无零点，则 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0
此时 SKIPIF 1 < 0 有两个零点，则 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0
则 SKIPIF 1 < 0
若 SKIPIF 1 < 0 有且仅有一个零点，则 SKIPIF 1 < 0 得 SKIPIF 1 < 0 ，
或 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，经检验 SKIPIF 1 < 0 不合题意
则 SKIPIF 1 < 0
此时 SKIPIF 1 < 0 有且仅有一个零点，则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 且 SKIPIF 1 < 0
则 SKIPIF 1 < 0 且 SKIPIF 1 < 0
综上所述： SKIPIF 1 < 0
故选：B．
2．（2022届高三数学新高考信息检测原创卷（四））已知 SKIPIF 1 < 0 是定义在 SKIPIF 1 < 0 上的奇函数， SKIPIF 1 < 0 是 SKIPIF 1 < 0 的导函数， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则不等式 SKIPIF 1 < 0 的解集是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【分析】根据题意，构造函数 SKIPIF 1 < 0 ，根据已知条件以及利用导数判断其单调性，从而求得 SKIPIF 1 < 0 的性质，再利用 SKIPIF 1 < 0 的性质求解不等式即可.
【详解】设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0
且 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减.
因为 SKIPIF 1 < 0 ，所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .
又当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以当 SKIPIF 1 < 0 时，恒有 SKIPIF 1 < 0 .
因为 SKIPIF 1 < 0 是 SKIPIF 1 < 0 上的奇函数，所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 等价于 SKIPIF 1 < 0 或 SKIPIF 1 < 0
解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
所以不等式 SKIPIF 1 < 0 的解集是 SKIPIF 1 < 0 .
故选：D.
【点睛】创新性考查落实，本题以函数导数为背景，考查函数奇偶性、利用导数研究函数单调性、二次不等式，考查运算求解能力，考查逻辑推理、数学建模、直观想象和数学运算核心素养.
3．已知函数 SKIPIF 1 < 0 有两个不同的极值点 SKIPIF 1 < 0 ，且不等式 SKIPIF 1 < 0 恒成立，则实数t的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【分析】把函数 SKIPIF 1 < 0 有两个不同的极值点 SKIPIF 1 < 0 转化为根的分布求出a的范围，
利用分离参数法得到 SKIPIF 1 < 0 .把 SKIPIF 1 < 0 转化为 SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，利用导数求出 SKIPIF 1 < 0 的值域，即可得到答案.
【详解】 SKIPIF 1 < 0 ，
因为函数 SKIPIF 1 < 0 有两个不同的极值点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以方程 SKIPIF 1 < 0 有两个不相等的正实数根，
于是有 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 .
因为不等式 SKIPIF 1 < 0 恒成立，
所以 SKIPIF 1 < 0 恒成立.
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ，
设 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，
故 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
因此实数t的取值范围是 SKIPIF 1 < 0 .
故选：A
【点睛】导数的应用主要有：
（1）利用导函数几何意义求切线方程；
（2）利用导数研究原函数的单调性，求极值（最值）；
（3）利用导数求参数的取值范围.
二、多选题
4．（河北省唐山市开滦第一中学2023届高三上学期第一次校际联考数学试题）若 SKIPIF 1 < 0 对任意 SKIPIF 1 < 0 恒成立，其中 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是整数，则 SKIPIF 1 < 0 的可能取值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】BCD
【分析】对 SKIPIF 1 < 0 分类讨论，当 SKIPIF 1 < 0 时，由 SKIPIF 1 < 0 可得 SKIPIF 1 < 0 ，由一次函数的图象知不存在；当 SKIPIF 1 < 0 时，由 SKIPIF 1 < 0 ，利用数形结合的思想可得出 SKIPIF 1 < 0 的整数解.
【详解】当 SKIPIF 1 < 0 时，由 SKIPIF 1 < 0 可得 SKIPIF 1 < 0 对任意 SKIPIF 1 < 0 恒成立，
即 SKIPIF 1 < 0 对任意 SKIPIF 1 < 0 恒成立，此时 SKIPIF 1 < 0 不存在；
当 SKIPIF 1 < 0 时，由 SKIPIF 1 < 0 对任意 SKIPIF 1 < 0 恒成立，
可设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，作出 SKIPIF 1 < 0 的图象如下，
由题意可知 SKIPIF 1 < 0 ，再由 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是整数可得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0
所以 SKIPIF 1 < 0 的可能取值为 SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0
故选：BCD
三、填空题
5．（重庆市南开中学校2023届高三上学期第三次质量检测数学试题）已知 SKIPIF 1 < 0 三个内角A，B，C的对边a，b，c依次成等比数列，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点T为线段AB（含端点）上的动点，若满足 SKIPIF 1 < 0 的点T恰好有2个，则实数t的取值范围为______．
【答案】 SKIPIF 1 < 0
【分析】由三角恒等变换与等比中项的性质可得 SKIPIF 1 < 0 为等边三角形，设BC中点M，则 SKIPIF 1 < 0 ，由题意若满足 SKIPIF 1 < 0 的点T恰好有2个，即需要 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，求解即可.
【详解】由 SKIPIF 1 < 0 ，
又由 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，或 SKIPIF 1 < 0 (舍).
SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，从而 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 为等边三角形．
设BC中点M，则 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
由题意若满足 SKIPIF 1 < 0 的点T恰好有2个，即需要 SKIPIF 1 < 0 ，
故 SKIPIF 1 < 0 ，
∴实数t的取值范围为 SKIPIF 1 < 0 ．
故答案为： SKIPIF 1 < 0 .
【点睛】本题的解题关键是将数量积 SKIPIF 1 < 0 转化为 SKIPIF 1 < 0 ，结合题意从而根据点到线段的距离以及几何知识可知
SKIPIF 1 < 0 的范围，再解不等式即可求出.