新高考数学一轮复习分层提升练习第08练 函数的基本性质Ⅱ-奇偶性、周期性和对称性（2份打包，原卷版+含解析）

这是一份新高考数学一轮复习分层提升练习第08练 函数的基本性质Ⅱ-奇偶性、周期性和对称性（2份打包，原卷版+含解析），文件包含新高考数学一轮复习分层提升练习第08练函数的基本性质Ⅱ-奇偶性周期性和对称性原卷版doc、新高考数学一轮复习分层提升练习第08练函数的基本性质Ⅱ-奇偶性周期性和对称性含解析doc等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。

一、单选题
1．（2023·北京通州·统考模拟预测）下列函数中，是奇函数且在定义域内单调递增的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【分析】根据幂函数、指数函数、正切函数的单调性及奇偶性逐一判断即可.
【详解】对于A，函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上递减，故A不符题意；
对于B，函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，关于原点对称，
因为 SKIPIF 1 < 0 ，所以函数为奇函数，
又函数在 SKIPIF 1 < 0 单调递增，故B符合题意；
对于C，函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，关于原点对称，
因为 SKIPIF 1 < 0 ，所以函数为偶函数，故C不符合题意；
对于D，函数 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，所以函数不是增函数，故D不符题意.
故选：B.
2．（2023春·河南·高三校联考阶段练习）已知 SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 都满足 SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A．3B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【分析】通过分析得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 .
【详解】根据题意， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，
所以函数 SKIPIF 1 < 0 的周期为6，所以 SKIPIF 1 < 0 ．
故选：D．
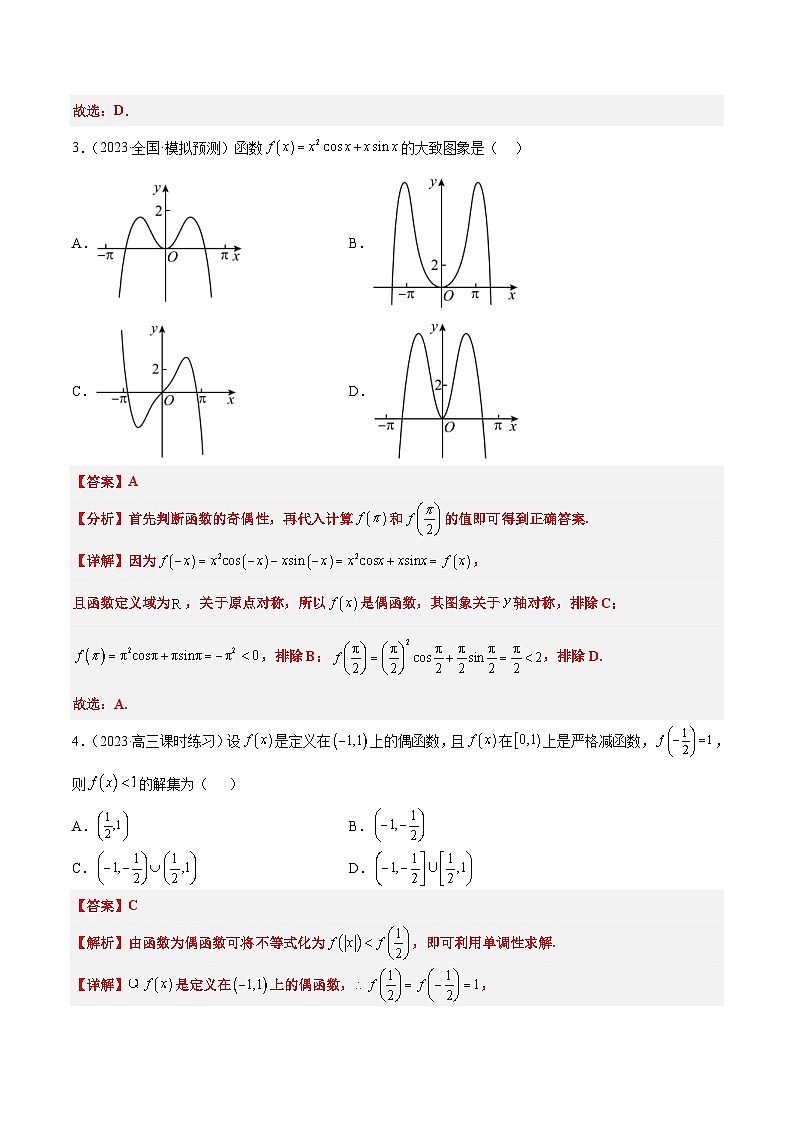
3．（2023·全国·模拟预测）函数 SKIPIF 1 < 0 的大致图象是（ ）
A．B．
C．D．
【答案】A
【分析】首先判断函数的奇偶性，再代入计算 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的值即可得到正确答案.
【详解】因为 SKIPIF 1 < 0 ，
且函数定义域为 SKIPIF 1 < 0 ，关于原点对称，所以 SKIPIF 1 < 0 是偶函数，其图象关于 SKIPIF 1 < 0 轴对称，排除C；
SKIPIF 1 < 0 ，排除B； SKIPIF 1 < 0 ，排除D.
故选：A.
4．（2023·高三课时练习）设 SKIPIF 1 < 0 是定义在 SKIPIF 1 < 0 上的偶函数，且 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上是严格减函数， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的解集为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【解析】由函数为偶函数可将不等式化为 SKIPIF 1 < 0 ，即可利用单调性求解.
【详解】 SKIPIF 1 < 0 SKIPIF 1 < 0 是定义在 SKIPIF 1 < 0 上的偶函数， SKIPIF 1 < 0 ，
则不等式 SKIPIF 1 < 0 为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上是严格减函数，
SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，又定义域为 SKIPIF 1 < 0 ，
故不等式的解集为 SKIPIF 1 < 0 .
故选：C.
【点睛】本题考查利用偶函数的性质解不等式，将不等式化为 SKIPIF 1 < 0 利用单调性求解是解题的关键.
5．（2023·浙江台州·统考二模）已知函数 SKIPIF 1 < 0 同时满足性质:① SKIPIF 1 < 0 ;②当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 ,则函数 SKIPIF 1 < 0 可能为( )
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【分析】① SKIPIF 1 < 0 说明 SKIPIF 1 < 0 为偶函数，② SKIPIF 1 < 0 ,说明函数在 SKIPIF 1 < 0 上单调递减,再逐项分析即可.
【详解】① SKIPIF 1 < 0 说明 SKIPIF 1 < 0 为偶函数，② SKIPIF 1 < 0 ,说明函数在 SKIPIF 1 < 0 上单调递减.
A不满足②，B不满足①，
C不满足②,因为 SKIPIF 1 < 0 在 SKIPIF 1 < 0 单调递减，在 SKIPIF 1 < 0 单调递增.
对于D,满足①,当 SKIPIF 1 < 0 ,单调递减,也满足②.
故选：D.
6．（2023·黑龙江大庆·铁人中学校考二模）已知函数 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，则实数a的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【分析】讨论 SKIPIF 1 < 0 与0、1的大小关系，写出 SKIPIF 1 < 0 的解析式，解出不等式后，再求并集即为答案.
【详解】因为 SKIPIF 1 < 0 .
①当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .
②当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .
③当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .
综上所述： SKIPIF 1 < 0 .
故选：D.
7．（2023春·江西·高三校联考阶段练习）设函数 SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称B． SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称
C． SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称D． SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称
【答案】D
【分析】根据函数对称性的性质依次判断选项即可得到答案.
【详解】对选项A，因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 不关于 SKIPIF 1 < 0 对称，故A错误.
对选项B，因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 不关于 SKIPIF 1 < 0 对称，故B错误.
对选项C，因为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 不关于 SKIPIF 1 < 0 对称，故C错误.
对选项D，因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，故D正确.
故选：D
8．（2023·青海·校联考模拟预测）已知函数 SKIPIF 1 < 0 为偶函数，且函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，则关于x的不等式 SKIPIF 1 < 0 的解集为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【分析】利用函数的奇偶性和对称性，得到函数的单调区间，利用单调性解函数不等式.
【详解】因为 SKIPIF 1 < 0 为偶函数，所以 SKIPIF 1 < 0 的图像关于y轴对称，则 SKIPIF 1 < 0 的图像关于直线 SKIPIF 1 < 0 对称．
因为 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减．
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ．
故选：A.
二、多选题
9．（2023·全国·高三专题练习）已知定义在 SKIPIF 1 < 0 上的奇函数 SKIPIF 1 < 0 的图象连续不断，且满足 SKIPIF 1 < 0 ，则以下结论成立的是（ ）
A．函数 SKIPIF 1 < 0 的周期 SKIPIF 1 < 0
B． SKIPIF 1 < 0
C．点 SKIPIF 1 < 0 是函数 SKIPIF 1 < 0 图象的一个对称中心
D． SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有4个零点
【答案】ABC
【分析】根据题意求得函数 SKIPIF 1 < 0 的周期为 SKIPIF 1 < 0 ，结合函数的周期性和 SKIPIF 1 < 0 ，逐项判定，即可求解.
【详解】由定义在 SKIPIF 1 < 0 上的奇函数 SKIPIF 1 < 0 的图象连续不断，且满足 SKIPIF 1 < 0 ，
所以函数 SKIPIF 1 < 0 的周期为 SKIPIF 1 < 0 ，所以A正确；
由 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，
又由 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，所以B正确；
由 SKIPIF 1 < 0 ，可得点 SKIPIF 1 < 0 是 SKIPIF 1 < 0 图象的一个对称中心，所以C正确；
由 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有 SKIPIF 1 < 0 ，
所以函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有5个零点，所以D错误.
故选：ABC.
10．（2023·全国·高三专题练习）已知定义在 SKIPIF 1 < 0 上的函数 SKIPIF 1 < 0 满足： SKIPIF 1 < 0 关于 SKIPIF 1 < 0 中心对称， SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，且 SKIPIF 1 < 0 .则下列选项中说法正确的有（ ）
A． SKIPIF 1 < 0 为奇函数B． SKIPIF 1 < 0 周期为2
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0 是奇函数
【答案】AD
【分析】由于 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，且关于 SKIPIF 1 < 0 中心对称，可知 SKIPIF 1 < 0 是奇函数，又 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，由此即可求出函数的周期，根据函数的奇偶性及周期性判断各项的正误.
【详解】由于 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，且关于 SKIPIF 1 < 0 中心对称，可得 SKIPIF 1 < 0 是奇函数，故A项正确；
因为 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 对称，即 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以函数 SKIPIF 1 < 0 的周期 SKIPIF 1 < 0 ，故B项错误；
SKIPIF 1 < 0 ，故C项错误；
SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 是奇函数，故D项正确.
故选：AD.
三、填空题
11．（2023秋·吉林长春·高三长春市第二中学校考期末）设 SKIPIF 1 < 0 是定义在 SKIPIF 1 < 0 上的奇函数，且 SKIPIF 1 < 0 ，又当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为______.
【答案】1
【分析】由已知可得函数的周期为4，然后根据函数解析式结合周期性奇偶性可求得结果.
【详解】因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 的周期为4，
因为 SKIPIF 1 < 0 是定义在 SKIPIF 1 < 0 上的奇函数，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ，
故答案为：1
12．（2023·全国·高三对口高考）已知函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是奇函数，且当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ________．
【答案】 SKIPIF 1 < 0
【分析】由奇函数性质得 SKIPIF 1 < 0 ，再根据奇函数求解析式即可.
【详解】解：因为 SKIPIF 1 < 0 为 SKIPIF 1 < 0 上的奇函数，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ．
所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 ．
所以， SKIPIF 1 < 0 时， SKIPIF 1 < 0
故答案为： SKIPIF 1 < 0
13．（2023·全国·高三专题练习）定义在 SKIPIF 1 < 0 上的奇函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为___________.
【答案】 SKIPIF 1 < 0
【分析】首先根据题意得到函数 SKIPIF 1 < 0 是以4为周期的周期函数，再结合奇函数的性质和对数的运算性质求解即可.
【详解】由题意，函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，
化简可得 SKIPIF 1 < 0 ，所以函数 SKIPIF 1 < 0 是以4为周期的周期函数，
因为 SKIPIF 1 < 0 为奇函数，
所以 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
14．（2023·福建漳州·统考三模）已知函数 SKIPIF 1 < 0 是定义在 SKIPIF 1 < 0 上的奇函数，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 _________.
【答案】 SKIPIF 1 < 0 / SKIPIF 1 < 0
【分析】根据奇函数的性质，结合题目中的函数解析式，可得答案.
【详解】由函数 SKIPIF 1 < 0 是定义在 SKIPIF 1 < 0 上的奇函数，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
15．（2023·全国·高三专题练习）已知函数 SKIPIF 1 < 0 ，若不等式 SKIPIF 1 < 0 在R上恒成立，则实数m的取值范围是________.
【答案】 SKIPIF 1 < 0 ．
【分析】利用换元法把目标式转化为二次函数问题，结合二次函数的单调性和最值情况可得答案.
【详解】令 SKIPIF 1 < 0
因为 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上是增函数，
所以 SKIPIF 1 < 0
因此要使 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上恒成立，应有 SKIPIF 1 < 0 ，即所求实数m的取值范围为 SKIPIF 1 < 0 ．
故答案为： SKIPIF 1 < 0 .
【B组 在综合中考查能力】
一、单选题
1．（2023·宁夏石嘴山·平罗中学校考模拟预测）如图是下列四个函数中的某个函数在区间 SKIPIF 1 < 0 上的大致图象，则该函数是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【分析】根据给定的函数图象特征，利用函数的奇偶性排除BC；利用 SKIPIF 1 < 0 的正负即可判断作答.
【详解】对于B， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 是偶函数，B不是；
对于C， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 是偶函数，C不是；
对于D， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，D不是；
对于A， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 是奇函数，
且 SKIPIF 1 < 0 ，A符合题意.
故选：A
2．（2023·上海宝山·统考二模）已知定义在 SKIPIF 1 < 0 上的偶函数 SKIPIF 1 < 0 ，若正实数a、b满足 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B．9C． SKIPIF 1 < 0 D．8
【答案】A
【分析】根据偶函数的对称性可得 SKIPIF 1 < 0 ，由题意分析可得 SKIPIF 1 < 0 ，结合基本不等式分析运算.
【详解】若函数 SKIPIF 1 < 0 为偶函数，则 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，
整理得 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 .
若正实数a、b满足 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，
可得 SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时，等号成立，
∴ SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0 .
故选：A.
3．（2023·广东广州·统考二模）已知偶函数 SKIPIF 1 < 0 与其导函数 SKIPIF 1 < 0 的定义域均为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 也是偶函数，若 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【分析】由偶函数的定义结合导数可得出 SKIPIF 1 < 0 ，由已知可得出 SKIPIF 1 < 0 ，可求出 SKIPIF 1 < 0 的表达式，利用导数分析函数 SKIPIF 1 < 0 的单调性，可知函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为增函数，再由 SKIPIF 1 < 0 可得出 SKIPIF 1 < 0 ，可得出关于实数 SKIPIF 1 < 0 的不等式，解之即可.
【详解】因为 SKIPIF 1 < 0 为偶函数，则 SKIPIF 1 < 0 ，等式两边求导可得 SKIPIF 1 < 0 ，①
因为函数 SKIPIF 1 < 0 为偶函数，则 SKIPIF 1 < 0 ，②
联立①②可得 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 不恒为零，
所以，函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为增函数，即函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为增函数，
故当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，所以，函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为增函数，
由 SKIPIF 1 < 0 可得 SKIPIF 1 < 0 ，
所以， SKIPIF 1 < 0 ，整理可得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 .
故选：B.
4．（2023·全国·模拟预测）已知函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是偶函数， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A．0B．1C．-1D．2
【答案】B
【分析】由函数的奇偶对称性推得 SKIPIF 1 < 0 是周期为4的函数，并求得 SKIPIF 1 < 0 ，最后利用周期性求目标函数值.
【详解】由 SKIPIF 1 < 0 是偶函数， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 是周期函数，周期为4，
对于 SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 SKIPIF 1 < 0 .
故选：B
5．（2023·新疆喀什·统考模拟预测）已知函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，满足 SKIPIF 1 < 0 为奇函数且 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 若 SKIPIF 1 < 0 则 SKIPIF 1 < 0 （ ）
A．10B．-10C． SKIPIF 1 < 0 D．- SKIPIF 1 < 0
【答案】A
【分析】根据函数 SKIPIF 1 < 0 的奇偶性与对称性得函数的周期，再根据已知区间内的解析式求得 SKIPIF 1 < 0 的值，最后利用周期性即可求得 SKIPIF 1 < 0 的值.
【详解】由 SKIPIF 1 < 0 为奇函数可得： SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ①，则 SKIPIF 1 < 0 关于点 SKIPIF 1 < 0 对称，令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；
由 SKIPIF 1 < 0 ②，得 SKIPIF 1 < 0 的图象关于直线 SKIPIF 1 < 0 对称；
由①②可得： SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，所以函数 SKIPIF 1 < 0 的周期 SKIPIF 1 < 0 ；
所以 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
联立 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 .所以 SKIPIF 1 < 0 .
故选：A.
二、多选题
6．（2023·山东菏泽·山东省东明县第一中学校联考模拟预测）已知函数 SKIPIF 1 < 0 的定义域为R， SKIPIF 1 < 0 为奇函数，且对 SKIPIF 1 < 0 ， SKIPIF 1 < 0 恒成立，则（ ）
A． SKIPIF 1 < 0 为奇函数B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】BCD
【分析】根据函数定义换算可得 SKIPIF 1 < 0 为偶函数，根据偶函数和奇函数性质可知 SKIPIF 1 < 0 为周期函数，再根据函数周期性和函数特殊值即可得出选项.
【详解】因为 SKIPIF 1 < 0 为奇函数，所以 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0
又 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为偶函数，A错误；
SKIPIF 1 < 0 为奇函数，所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，B正确；
SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 的图象关于点 SKIPIF 1 < 0 对称，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，C正确；
又 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 是以4为周期的函数，
SKIPIF 1 < 0 ，D正确．
故选：BCD．
7．（2023·江苏·统考三模）已知函数 SKIPIF 1 < 0 及其导函数 SKIPIF 1 < 0 的定义域均为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】BC
【分析】本题根据函数对称性，周期性与导数与单调性相关知识可得结果.
【详解】因 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，又因 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，所以 SKIPIF 1 < 0 的周期为4，
A：因 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，故A错．
B：当 SKIPIF 1 < 0 时 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
因 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，故B正确.
C： SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称且关于 SKIPIF 1 < 0 对称，所以 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，即 SKIPIF 1 < 0 为奇函数， SKIPIF 1 < 0 为偶函数，故C正确.
D：因 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减， SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，因 SKIPIF 1 < 0 的周期为4，所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，所以 SKIPIF 1 < 0 ，D错误.故选：BC.
三、填空题
8．（2023春·上海虹口·高三统考期中）对于定义在 SKIPIF 1 < 0 上的奇函数 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则该函数的值域为________.
【答案】 SKIPIF 1 < 0
【分析】根据奇函数的性质求得 SKIPIF 1 < 0 ，再结合基本不等式求 SKIPIF 1 < 0 时其 SKIPIF 1 < 0 的取值范围，再结合奇函数的性质求 SKIPIF 1 < 0 时函数值的范围，由此可得函数值域.
【详解】因为 SKIPIF 1 < 0 为 SKIPIF 1 < 0 上的奇函数，
所以 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
又当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 时等号成立，
即当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 为 SKIPIF 1 < 0 上的奇函数，
所以函数 SKIPIF 1 < 0 的图象关于原点对称，
所以 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以函数 SKIPIF 1 < 0 的值域为 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
9．（2023·吉林通化·梅河口市第五中学校考模拟预测）某函数 SKIPIF 1 < 0 满足以下三个条件：
① SKIPIF 1 < 0 是偶函数；② SKIPIF 1 < 0 ；③ SKIPIF 1 < 0 的最大值为4．
请写出一个满足上述条件的函数 SKIPIF 1 < 0 的解析式______．
【答案】 SKIPIF 1 < 0 （答案不唯一）
【分析】根据所给条件分析函数的性质，结合所学函数可得.
【详解】因为 SKIPIF 1 < 0 是偶函数，所以 SKIPIF 1 < 0 的图象关于y轴对称，
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0
所以 SKIPIF 1 < 0 的图象关于点 SKIPIF 1 < 0 对称，所以4为 SKIPIF 1 < 0 的一个周期，
又 SKIPIF 1 < 0 的最大值为4，所以 SKIPIF 1 < 0 满足条件.
故答案为： SKIPIF 1 < 0 （答案不唯一）
10．（2023·陕西咸阳·统考三模）已知 SKIPIF 1 < 0 是定义在R上的偶函数，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则不等式 SKIPIF 1 < 0 的解集是________．
【答案】 SKIPIF 1 < 0
【分析】利用导数判断当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 的单调性，结合偶函数解不等式.
【详解】当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，
因为 SKIPIF 1 < 0 是定义在R上的偶函数，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，
若 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
可得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
所以不等式 SKIPIF 1 < 0 的解集是 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
11．（2023·全国·高三专题练习）若 SKIPIF 1 < 0 为定义在 SKIPIF 1 < 0 上的连续不断的函数，满足 SKIPIF 1 < 0 ，且当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围___________.
【答案】 SKIPIF 1 < 0
【分析】构造函数 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 为奇函数，再利用导数判断函数 SKIPIF 1 < 0 的单调性，再根据函数的奇偶性和单调性即可求解.
【详解】由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，
设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为奇函数，
又 SKIPIF 1 < 0 ， SKIPIF 1 < 0 在 SKIPIF 1 < 0 上是减函数，从而在 SKIPIF 1 < 0 上是减函数，
则 SKIPIF 1 < 0 ，
等价于 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 的取值范围为 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
四、解答题
12．（2023·河北·高三学业考试）已知二次函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 的解析式；
(2)若方程 SKIPIF 1 < 0 ， SKIPIF 1 < 0 时有唯一一个零点，且不是重根，求 SKIPIF 1 < 0 的取值范围；
(3)当 SKIPIF 1 < 0 时，不等式 SKIPIF 1 < 0 恒成立，求实数 SKIPIF 1 < 0 的范围．
【答案】(1) SKIPIF 1 < 0
(2) SKIPIF 1 < 0
(3) SKIPIF 1 < 0
【分析】（1）设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，得到 SKIPIF 1 < 0 ，代入函数计算得到 SKIPIF 1 < 0 ，得到解析式.
（2）令 SKIPIF 1 < 0 ，只需 SKIPIF 1 < 0 ，解不等式并验证得到答案.
（3）设 SKIPIF 1 < 0 ，确定函数的单调性，计算最值得到答案.
【详解】（1）设 SKIPIF 1 < 0 ，则由 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 的解析式为 SKIPIF 1 < 0 ．
（2）令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有唯一零点且不是重根，
只需 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
经检验 SKIPIF 1 < 0 时，方程 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有唯一解 SKIPIF 1 < 0 ；
SKIPIF 1 < 0 时，方程 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有唯一解 SKIPIF 1 < 0 ，
故实数 SKIPIF 1 < 0 的取值范围为 SKIPIF 1 < 0 ．
（3） SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立，即 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立．
设 SKIPIF 1 < 0 ，其图象的对称轴为直线 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减．
故只需 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ， SKIPIF 1 < 0
【C组 在创新中考查思维】
一、单选题
1．（2023·辽宁·校联考二模）设函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上满足 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且在闭区间 SKIPIF 1 < 0 上只有 SKIPIF 1 < 0 ，则方程 SKIPIF 1 < 0 在闭区间 SKIPIF 1 < 0 上的根的个数（ ）．
A．1348B．1347C．1346D．1345
【答案】B
【分析】根据周期函数性质可知，只需求出一个周期里的根的个数，可求得 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的零点个数，再分区间 SKIPIF 1 < 0 和 SKIPIF 1 < 0 讨论即可.
【详解】 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上满足 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 和直线 SKIPIF 1 < 0 对称，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 的周期为6，
又在闭区间 SKIPIF 1 < 0 上只有 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
且当 SKIPIF 1 < 0 时，通过其关于直线 SKIPIF 1 < 0 对称，得其 SKIPIF 1 < 0 值对应着 SKIPIF 1 < 0 的 SKIPIF 1 < 0 值，
则 SKIPIF 1 < 0 在闭区间 SKIPIF 1 < 0 上只有 SKIPIF 1 < 0 ，
同理可推得 SKIPIF 1 < 0 在 SKIPIF 1 < 0 也只有两个零点，
因为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 共有 SKIPIF 1 < 0 个零点，
因为 SKIPIF 1 < 0 ，且在 SKIPIF 1 < 0 的图象与 SKIPIF 1 < 0 的图象相同，
则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有 SKIPIF 1 < 0 个零点，
则方程 SKIPIF 1 < 0 在闭区间 SKIPIF 1 < 0 上的根的个数为1347个.
故选：B.
【点睛】思路点睛：利用零点存在性定理不仅要函数在区间[a,b]上是连续不断的曲线，且f(a)·f(b)<0，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点．
2．（2023·新疆·统考二模）设 SKIPIF 1 < 0 是定义在R上的以2为周期的偶函数，在区间 SKIPIF 1 < 0 上单调递减，且满足 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则不等式组 SKIPIF 1 < 0 的解集为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【分析】根据题意，由函数的周期性与奇偶性分析可得 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 对称，据此可得 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上递增，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则进而分析 SKIPIF 1 < 0 可得答案．
【详解】根据题意， SKIPIF 1 < 0 为周期为2的偶函数，
则 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，
则有 SKIPIF 1 < 0 ，
则函数 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 对称，
又由 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上单调递减，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
因为周期为2得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 对称，则 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上递增，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，即不等式组的解集为 SKIPIF 1 < 0 .
故选：D．
3．（2023·海南·海口市琼山华侨中学校联考模拟预测）设偶函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的导函数为 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时，有 SKIPIF 1 < 0 ，则下列结论一定正确的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【分析】将 SKIPIF 1 < 0 变形为 SKIPIF 1 < 0 ，从而可构造函数 SKIPIF 1 < 0 ，判断其单调性以及奇偶性，由此代入数值，一一判断各选项，即可得答案.
【详解】当 SKIPIF 1 < 0 时，有 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，
又 SKIPIF 1 < 0 为偶函数，则 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 为偶函数，
故 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，故A错误，C正确；
由 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，B错误；
而 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 不一定成立，D错误，
故选：C
【点睛】关键点睛：解答本题的关键在于要能根据已知不等式的结构特征，进行变形，从而构造出函数 SKIPIF 1 < 0 ，进而判断其单调性，即可解决问题.
二、多选题
4．（2023·江苏·统考二模）已知函数 SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 是偶函数，也是周期函数B． SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0
C． SKIPIF 1 < 0 的图像关于直线 SKIPIF 1 < 0 对称D． SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增
【答案】BD
【分析】根据奇偶函数的定义即可判断A，求导得到 SKIPIF 1 < 0 ，从而得到其极值，即可判断B，根据对称性的定义即可判断C，由 SKIPIF 1 < 0 在 SKIPIF 1 < 0 的正负性即可判断D.
【详解】因为 SKIPIF 1 < 0 ，定义域为 SKIPIF 1 < 0 ，关于原点对称，
且 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 是奇函数，故A错误；
因为 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 单调递增，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 单调递减，
所以 SKIPIF 1 < 0 ，故B正确；
因为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以不关于 SKIPIF 1 < 0 对称，故C错误；
因为 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，故D正确.
故选:BD
三、填空题
5．（2023·全国·模拟预测）已知函数 SKIPIF 1 < 0 及其导函数 SKIPIF 1 < 0 的定义域均为R，且满足 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．若不等式 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立，则a的取值范围是__________,
【答案】 SKIPIF 1 < 0
【分析】构造 SKIPIF 1 < 0 ，得到其奇偶性和单调性，对不等式变形得到 SKIPIF 1 < 0 ，从而得到 SKIPIF 1 < 0 ，平方后由一次函数的性质得到不等式组，求出a的取值范围.
【详解】令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 为R上的偶函数，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 单调递减，在 SKIPIF 1 < 0 单调递增．
SKIPIF 1 < 0 等价于 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立．
所以 SKIPIF 1 < 0 ，平方后化简得到 SKIPIF 1 < 0 ．
由一次函数性质可得 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
故a的取值范围是 SKIPIF 1 < 0 ．
故答案为： SKIPIF 1 < 0 .
【点睛】利用函数 SKIPIF 1 < 0 与导函数 SKIPIF 1 < 0 的相关不等式构造函数，然后利用所构造的函数的单调性解不等式，是高考常考题目，以下是构造函数的常见思路：
比如：若 SKIPIF 1 < 0 ，则构造 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，则构造 SKIPIF 1 < 0 ，
若 SKIPIF 1 < 0 ，则构造 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，则构造 SKIPIF 1 < 0 .
四、解答题
6．（2023·全国·高三专题练习）已知定义在 SKIPIF 1 < 0 上的偶函数 SKIPIF 1 < 0 和奇函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 .
(1)求函数 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的解析式：
(2)若函数 SKIPIF 1 < 0 |的最小值为 SKIPIF 1 < 0 ，求实数m的值.
【答案】(1) SKIPIF 1 < 0
(2) SKIPIF 1 < 0 .
【分析】（1）根据函数奇偶性得到方程组 SKIPIF 1 < 0 ，解出即可.
（2）首先分类讨论去绝对值，得到 SKIPIF 1 < 0 ，通过整体换元令 SKIPIF 1 < 0 ，则得到 SKIPIF 1 < 0 ，再次分类讨论，分 SKIPIF 1 < 0 ， SKIPIF 1 < 0 和 SKIPIF 1 < 0 讨论即可.
【详解】（1）由 SKIPIF 1 < 0 可得 SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 是偶函数和 SKIPIF 1 < 0 是奇函数，故 SKIPIF 1 < 0 .
由 SKIPIF 1 < 0 解得 SKIPIF 1 < 0 .
（2） SKIPIF 1 < 0
SKIPIF 1 < 0
令 SKIPIF 1 < 0 ，易得 SKIPIF 1 < 0 在R上是增函数，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 .
SKIPIF 1 < 0
令 SKIPIF 1 < 0
SKIPIF 1 < 0
若 SKIPIF 1 < 0 ，则此时 SKIPIF 1 < 0 ，不合题意，舍去
若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
∴ SKIPIF 1 < 0 .
【点睛】方法点睛：（1）常见的求解函数解析式的方法：①换元法；②配方法；③方程组法；④待定系数法；
（2）对于带有绝对值的函数首先要去绝对值分类讨论，若此时边界值依旧含参数，需要再次进行分类讨论；
（3）遇到题目中一个较长代数式含有多组 SKIPIF 1 < 0 ，我们通常利用换元法令 SKIPIF 1 < 0 ，并要注意 SKIPIF 1 < 0 的范围.