
2023-2024学年湖北省武汉市汉阳区八年级(下)期末数学试卷(含详细答案解析) (1)
展开1.− 4的相反数是( )
A. 4B. −2C. 2D. −4
2.下列二次根式中,x的取值范围是x≥3的是( )
A. 3−xB. 6+2xC. x−3D. x+3
3.矩形具有而菱形不具有的性质是( )
A. 两组对边分别平行B. 对角线相等C. 对角线互相平分D. 两组对角分别相等
4.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是( )
A. 1cm
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A. 平均数B. 众数C. 中位数D. 方差
6.下列式子是最简二次根式的是( )
A. 12B. 2C. a2D. 8
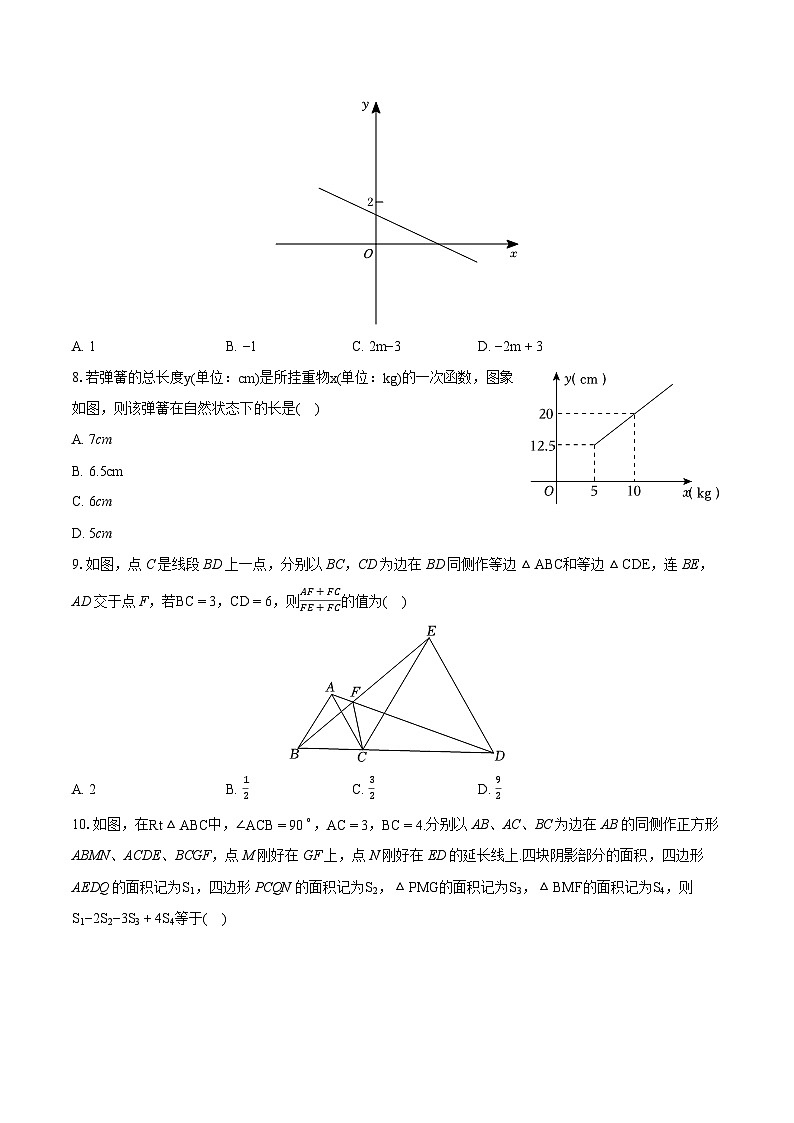
7.一次函数y=(1−m)x+m的图象如图所示,则化简|1−m|+ m2−4m+4的结果是( )
A. 1B. −1C. 2m−3D. −2m+3
8.若弹簧的总长度y(单位:cm)是所挂重物x(单位:kg)的一次函数,图象如图,则该弹簧在自然状态下的长是( )
A. 7cm
B. 6.5cm
C. 6cm
D. 5cm
9.如图,点C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,连BE,AD交于点F,若BC=3,CD=6,则AF+FCFE+FC的值为( )
A. 2B. 12C. 32D. 92
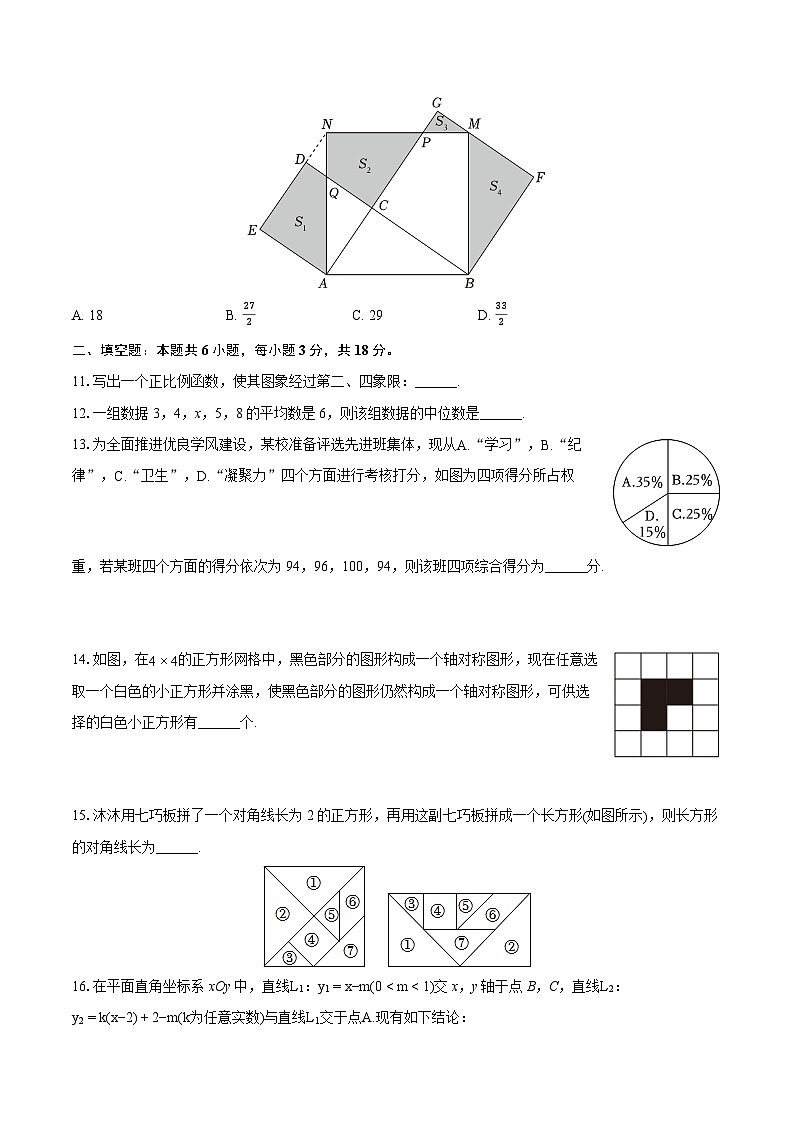
10.如图,在Rt△ABC中,∠ACB=90∘,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABMN、ACDE、BCGF,点M刚好在GF上,点N刚好在ED的延长线上.四块阴影部分的面积,四边形AEDQ的面积记为S1,四边形PCQN的面积记为S2,△PMG的面积记为S3,△BMF的面积记为S4,则S1−2S2−3S3+4S4等于( )
A. 18B. 272C. 29D. 332
二、填空题:本题共6小题,每小题3分,共18分。
11.写出一个正比例函数,使其图象经过第二、四象限:______.
12.一组数据3,4,x,5,8的平均数是6,则该组数据的中位数是______.
13.为全面推进优良学风建设,某校准备评选先进班集体,现从A.“学习”,B.“纪律”,C.“卫生”,D.“凝聚力”四个方面进行考核打分,如图为四项得分所占权重,若某班四个方面的得分依次为94,96,100,94,则该班四项综合得分为______分.
14.如图,在4×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形,可供选择的白色小正方形有______个.
15.沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为______.
16.在平面直角坐标系xOy中,直线L1:y1=x−m(0
③k≠1,若直线L2与y轴交点为D,△ADC为等腰直角三角形,DC的长为2或4;
④关于x,y的二元一次方程组y=x−my=k(x−2)+2−m一定有一组解的x=2.
其中正确的结论序号为______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
已知一次函数的图象经过点(−4,9)和点(6,3),求这个函数的解析式.
18.(本小题8分)
如图,▱ABCD中,AC,BD相交于点O,点E,F分别是OA,OC的中点.
(1)求证:四边形DEBF为平行四边形;
(2)设ACBD=k,当k为何值时,四边形DEBF是矩形?请直接写出合适的k值.不需要说明理由.
19.(本小题8分)
读书可以让人得到智慧启发.学校某兴趣小组为了了解学生课外阅读的情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
【收集数据】从学校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如表(单位:min):
【整理数据】按下表分段整理样本数据:
【分析数据】对样本数据进行分析得到如下分析表:
【得出结论】
(1)补全分析表中的数据:a=______,m=______,n=______;
(2)如果该校现有学生1600人,请估计每周阅读时间超过90min的学生有多少人;
(3)假设平均阅读一本课外书的时间为310分钟,请你估计该校学生每人半年(按24周计算)平均阅读多少本课外书.
20.(本小题8分)
已知:正方形ABCD的边长是4,F是DC边的中点,E是BC上的点,且CE=14BC,如图,求证:∠AFE=90∘.
21.(本小题8分)
如图是由小正方形组成的9×7网格,每个小正方形的顶点叫做格点.图中A,C都是格点,仅用无刻度的直尺在给定网格中完成画图.
(1)在图1中,点B是格点,点D是BC与网格线的交点,先画格点E,使AE⊥AB于点A,且AE=AB,再连AE,在AE上画点F,使DF//AB;
(2)在图2中,点G为格线上的非格点,先画线段AG中点H,再画线段AP,使AP//CG,且AP=CG.
22.(本小题10分)
方便便捷的生活方式,极大的方便了我们生活,你是否知道营业厅电话营销的基本常识:营业厅的月使用费用固定收取,当选择了这个套餐,业务开通后,不论是否通话都会按规定收费;主叫限定时间,是电话通信的一种优惠方式,在不超过主叫限定时间内主叫通话不再收费,主叫超时部分加收超时费,被叫免费.某营业厅有如下两种移动电话计费方式:
若选择某种套餐后,主叫时间为t分钟,计费的总费用为y元.
(1)分别直接写出套餐A和套餐B的总费用yA,yB与t间的函数关系式;
(2)是否存在实数t,使选择套餐A或B,费用相同,若存在,求主叫通话时间,若不存在,请说明理由;
(3)营业厅的工作人员推销说,对于套餐A和套餐B,加收的主叫超时费用套餐A总比套餐B多,请你通过计算或推理的分式说明工作人员是否有欺骗消费者的意图,并说明如何选择哪种套餐更省钱.
23.(本小题10分)
(1)已知点D为等边△ABC边AB所在直线上一点,连DC,以DC为边作等边△DEC,连AE.
①如图1,点D在线段AB上,求证:AE//BC;
②如图2,点D在AB的延长线上,F,G分别是BE,AD的中点,连FG,求FGAE的值;
(2)如图3,点D为等腰直角△ABC直角边AB所在直线上任意一点,连CD,以CD为斜边作等腰直角△CDE,连BE,当CE的长最小时,直接写出CEBE的值,不需要说明理由.
24.(本小题12分)
如图,在平面直角坐标系中,点O为坐标原点,直线m:y=12x+1交x,y轴于A,B,直线n:y=kx+2k(k为任意常实数).
(1)直接写出点A,B坐标和线段AB的长;
(2)第四象限的直线n上存在点P,使∠APB=45∘,且AB=BP,求直线n的解析式;
(3)如图2,直线y=−2x+2上有一点E,D(0,−3),过(4,0)且平行于y轴的直线上有点F,若△DEF为等腰直角三角形,且∠DEF=90∘,直接写出E点坐标.
答案和解析
1.【答案】C
【解析】解:∵− 4=−2,−2的相反数是2,
∴− 4的相反数是2.
故选:C.
先由算术平方根的定义求出 4=2,再根据相反数的定义即可求解.
本题考查了算术平方根与相反数的定义,比较简单.
2.【答案】C
【解析】解:A、根据二次根式有意义的条件可得:3−x≥0,解得x≤3,故此选项错误;
B、根据二次根式有意义的条件可得:6+2x≥0,解得x≥−3,故此选项错误;
C、根据二次根式有意义的条件可得:x−3≥0,解得x≥3,故此选项正确;
D、根据二次根式有意义的条件可得:x+3≥0,解得x≥−3,故此选项错误;
故选:C.
根据二次根式有意义的条件:被开方数是非负数分别进行分析.
此题主要考查了二次根式有意义的条件,关进是掌握二次根式中的被开方数是非负数.
3.【答案】B
【解析】解:A、矩形与菱形的两组对边都分别平行,故本选项错误;
B、矩形的对角线相等,菱形的对角线不一定相等,故本选项正确;
C、矩形与菱形的对角线都互相平分,故本选项错误;
D、矩形与菱形的两组对角都分别相等,故本选项错误.
故选B.
根据矩形与菱形的性质对各选项分析判断后利用排除法求解.
本题考查了矩形的性质,菱形的性质,熟记两图形的性质是解题的关键.
4.【答案】A
【解析】【分析】
根据三角形的三边关系定理得到AC的取值范围,再根据平行四边形的性质即可求出OA的取值范围.
本题考查了对平行四边形的性质,三角形的三边关系定理等知识点的理解和掌握,得到AO是AC的一半是解此题的关键.
【解答】
解:∵AB=3cm,BC=5cm,
∴2cm
∴AO=12AC,
∴1cm
5.【答案】C
【解析】解:去掉一个最高分和一个最低分对中位数不发生变化;
故选:C.
根据中位数的定义:位于中间位置或中间两数的平均数可以得到去掉一个最高分和一个最低分不影响中位数.
本题考查了统计量的选择,解题的关键是了解中位数的定义,难度不大.
6.【答案】B
【解析】解:A、 12= 22,被开方数含分母,不是最简二次根式;
B、 2是最简二次根式;
C、 a2=|a|,被开方数中含能开得尽方的因式,不是最简二次根式;
D、 8=2 2,被开方数中不含能开得尽方的因数,不是最简二次根式;
故选:B.
根据最简二次根式的概念判断即可.
本题考查的是最简二次根式的概念,最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.
7.【答案】A
【解析】解:由题意得,1−m<00
=1.
故选A.
根据一次函数的图象确定m的取值范围,再化简即可.
本题主要考查了一次函数图象与系数的关系,解题的关键是求出m的取值范围.
8.【答案】D
【解析】解:设一次函数的解析式为y=kx+b,
把(5,12.5)、(10,20)代入,
得5k+b=12.510k+b=20,
解得k=1.5b=5,
∴一次函数的解析式为y=1.5x+5,
当x=0时,y=5,
即不挂重物时,弹簧的长度是5cm.
故选:D.
利用待定系数法求出过(5,12.5)、(10,20)两点的一次函数的解析式为y=0.5x+10,当不挂重物时,即x=0,代入解析式求出对应的函数值即可弹簧的长度.
本题考查了一次函数的应用:运用一次函数的性质,把实际问题与函数图象结合进行分析,从函数图象中获取实际问题中的数据,把实际问题中的数据转化为函数图象中的点的坐标,并且运用一次函数图象描树实际问题.也考查了待定系数法求函数的解析式.
9.【答案】B
【解析】解:∵△ABC和△CDE为等边三角形,
∴∠ACB=∠ECD=60∘,AC=BC,CE=CD.
∵∠BCE=∠ACB+∠ACE,∠ACD=∠ECD+∠ACE,
∴∠BCE=∠ACD,∠ACE=180∘−60∘−60∘.
又∵AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS).
∴∠CEB=∠CDA.
如图,在FD上取一点G,连接EG,使FG=EF.
∵∠ECD=∠EBC+∠CEB=60∘,
∴∠EFD=∠EBC+∠CDA=60∘.
∵FG=EF,
∴△EFG是等边三角形.
∴EF=EG,∠GEF=60∘.
∵∠CED=∠GEF=60∘,
∴∠CED−∠GEC=∠GEF−∠GEC.
∴∠FEC=∠GED.
又∵ED=EC,
∴△EFC≌△EGD(SAS).
∴∠FCE=∠GDE.
∵∠ACB=∠EDC=60∘,
∴ED//AC.
∴∠EDG=∠CAF.
∴△AFC∽△CFE.
∴AFFC=FCEF=ACEC.
∵AC=BC=3,EC=CD=6,
∴AFFC=FCEF=36=12.
∴FC=2AF,EF=2FC.
∴AF+FCFE+FC=AF+2AF4AF+2AF=3AF6AF=12.
故选:B.
依据题意,根据△ABC和△CDE为等边三角形,先证明△ACD≌△BCE,可得∠CEB=∠CDA,再在FD上取一点G,连接EG,使FG=EF,从而可得△EFG是等边三角形,再证明△EFC≌△EGD,则∠FCE=∠GDE,又ED//AC,可得△AFC∽△CFE进而可得AFFC=FCEF=ACEC,再由AC=BC=3,EC=CD=6,故AFFC=FCEF=36=12,又FC=2AF,EF=2FC,进而代入计算可以得解.
本题主要考查了全等三角形的判定与性质、相似三角形的判定与性质、等边三角形的性质,解题时要熟练掌握并能灵活运用是关键.
10.【答案】D
【解析】解:∵∠ACB=90∘,AC=3,BC=4.
∴AB=5.
∵四边形ABMN、四边形ACDE、四边形BCGF为正方形,
∴BM=MN=AN=5,AC=AE=DE=DC=3,BF=GF=4,∠F=∠G=∠ANP=∠E=∠ACD=∠BMN=90∘.
∴MF= BM2−BF2=3,∠MBF+∠BMF=90∘,∠BMF+∠PMG=90∘,∠PMG+∠GPM=90∘,∠GPM=∠APN,∠APN+∠NAG=90∘.
∴GM=1,∠MBF=∠GMP=∠NAC.
∴tan∠MBF=tan∠GMP=tan∠NAC.
∴MFBF=GPGM=PNAN=CQCA.
∴34=GP1=PN5=CQ3.
解得:GP=34,PN=154,CQ=94.
∴S1=32−12×3×94=458,S2=12×5×154−12×94×3=6,S3=12×1×34=38,S4=12×3×4=6.
∴S1−2S2−3S3+4S4=458−2×6−3×38+4×6=332.
故选:D.
根据勾股定理可得MF=3,那么GM=1,易得∠MBF=∠GMP=∠NAC,那么这几个角的正切值也相等,可计算出GP、PN、CQ的长度,分别计算出S1、S2、S3、S4的长度,代入所求的式子计算即可.
本题考查勾股定理及解直角三角形的应用.关键是判断出图形中相等的角,使用相等的角的正切值得到相关线段的长度.
11.【答案】y=−x(答案不唯一)
【解析】先设出此正比例函数的解析式,再根据正比例函数的图象经过二、四象限确定出k的符号,再写出符合条件的正比例函数即可.
解:设此正比例函数的解析式为y=kx(k≠0),
∵此正比例函数的图象经过二、四象限,
∴k<0,
∴符合条件的正比例函数解析式可以为:y=−x(答案不唯一).
故答案为:y=−x(答案不唯一).
本题考查的是正比例函数的性质,即正比例函数y=kx(k≠0)中,当k<0时函数的图象经过二、四象限.
12.【答案】5
【解析】解:由题意知3+4+x+5+8=6×5,
解得x=10,
则这组数据为3,4,5,8,10,
∴这组数据的中位数为5,
故答案为:5.
先根据平均数的定义求出x的值,得出这组数据,再根据中位数的定义求解可得.
此题主要考查了一组数据平均数的求法以及中位数的求法,又结合了实际问题,此题比较典型.
13.【答案】96
【解析】解:该班四项综合得分为94×35%+96×25%+100×25%+94×15%=96(分),
故答案为:96.
根据加权平均数的定义列式计算即可.
本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
14.【答案】5
【解析】解:如图所示:标有数字的5个位置都是轴对称图形.
故答案为:5.
直接利用轴对称图形的定义进而得出符合题意的答案.
此题主要考查了利用轴对称设计图案,正确把握轴对称图形的定义是解题关键.
15.【答案】 5
【解析】解:根据图形可知:长方形的长是正方形的对角线为2,
长方形的宽是正方形对角线的一半为1,
则长方形的对角线长= 12+22= 5.
故答案为: 5.
根据图形可得长方形的长是正方形的对角线为2,长方形的宽是正方形对角线的一半为1,然后利用勾股定理即可解决问题.
本题考查了正方形的性质,七巧板,矩形的性质,解决本题的关键是掌握正方形的性质.
16.【答案】②③④
【解析】解:①∵直线L1:y1=x−m(0
∴y1随x的增大而增大,
当x=0时,y1=−m;当x=1时,y1=1−m,
∴−m
③∵x=2时,y1=x−m,y2=2−m,
∴A(2,2−m),
当∠ADC=90∘时,
∵△ADC为等腰直角三角形,
∴DC=AD=2;
当∠DAC=90∘时,
∵△ADC为等腰直角三角形,
∴DC=4;
∴DC的长为2或4,故结论③正确;
④由③可知,直线L1与直线L2的交点A横坐标为2,
∴关于x,y的二元一次方程组y=x−my=k(x−2)+2−m一定有一组解的x=2,故结论④正确.
故答案为:②③④.
利用一次函数图象上点的坐标特征即可判断①;由一次项系数即可判断②;分两组情况讨论求得CD的值即可判断③;根据A的横坐标即可判断④.
本题考查的是一次函数与二元一次方程组,一次函数的性质,一次函数图象上点的坐标特征,等腰直角三角形的性质等,求得A点的坐标是解题的关键.
17.【答案】解:设函数解析式为y=kx+b,
∵一次函数的图象经过点(−4,9)和点(6,3),
∴−4k+b=96k+b=3,
解得k=−35b=335,
所以,这个函数的解析式为y=−35x+335.
【解析】本题考查了待定系数法求一次函数解析式,待定系数法是求函数解析式常用的方法,一定要熟练掌握.
设函数解析式为y=kx+b,把经过的两个点的坐标代入得到关于k、b的二元一次方程组,求解得到k、b的值,即可得解.
18.【答案】(1)证明:∵四边形ABCD是平行四边形,AC,BD相交于点O,
∴OA=OC,OB=OD,
∴12OA=12OC,
∵点E,F分别是OA,OC的中点,
∴OE=12OA,OF=12OD,
∴OE=OF,
∵OB=OD,OE=OF,
∴四边形DEBF为平行四边形.
(2)当k=2时,四边形DEBF是矩形,
理由:∵ACBD=k=2,
∴AC=2BD,
∵AE=OE=OF=CF,
∴AC=4OE,
∵BD=2OB,
∴4OE=2×2OB,
∴OE=OB,
∴2OE=2OB,
∵EF=2OE,BD=2OB,
∴EF=BD,
∵四边形DEBF是平行四边形,且EF=BD,
∴四边形DEBF是矩形.
【解析】(1)由平行四边形的性质得OA=OC,OB=OD,因为OE=12OA,OF=12OD,所以OE=OF,即可由OB=OD,OE=OF,证明四边形DEBF为平行四边形;
(2)当ACBD=k=2时,则AC=2BD,因为AC=4OE,BD=2OB,所以4OE=2×2OB,则OE=OB,所以EF=BD,即可证明四边形DEBF是矩形.
此题重点考查平行四边形的判定与性质、矩形的判定定理等知识,推导出OE=OB是解题的关键.
19.【答案】481min81min
【解析】解:(1)a=4,m=81+812=81(min),众数为81min.
故答案为:4,81min,81min;
(2)1600×720=560(人);
答:该校现有学生1600人,每周阅读时间超过90min的学生约为560人;
(3)77.5×24÷310=6(本).
答:估计该校学生每人半年(按24周计算)平均阅读6本课外书
(1)a=20−5−7−4=4,再根据中位数,众数的定义求出m,n;
(2)1600×90min以上的人数20,可得结论;
(3)选择“平均数”进行计算即可.
本题考查众数,样本估计总体,频数分布表,平均数、中位数等众数,掌握计算方法是正确解答的关键.
20.【答案】证明:∵CE=14BC,
∴CE=1,BE=3,
∵F是DC边的中点,
∴CF=DF=2,
在Rt△ABE中,∠B=90∘,
由勾股定理得:AE2=32+42=25,
在Rt△ECF中,∠C=90∘,
由勾股定理得:FE2=12+22=5,
在Rt△ADF中,∠D=90∘,
由勾股定理得:AF2=42+22=20,
∴AE2=FE2+AF2,
∴AF⊥EF,
∴∠AFE=90∘.
【解析】求出△AEF各边的长度,运用勾股定理逆定理解决.
本题考查了正方形的性质、勾股定理及其逆定理,熟练掌握勾股定理和逆定理是解决本题的关键.
21.【答案】解:(1)如图1中,线段AE,点F即为所求;
(2)如图2中,点H,线段AP即为所求.
【解析】(1)利用旋转变换的性质作出线段AE即可,取格点K,连接AK交网格线于点Q,连接DQ交AE于点F,点F即为所求;
(2)取网格线的中点J,K,作直线JK交AB于点H,取AC的中点O,连接GO交网格线于点P,连接AP,线段AP即为所求.
本题考查作图-应用与设计作图,平行线的判定和性质,线段垂直平分线的性质,等腰直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
22.【答案】解:(1)当t≤150时,yA=58,
当t>150时,yA=58+0.25(t−150)=0.25t+20.5,
∴yA=58(t≤150)0.25t+20.5(t>150),
当t≤350时,yB=88,
当t>350时,yB=88+0.19(t−350)=0.19t+21.5,
∴yB=88(t≤350)0.19t+21.5(t>350).
(2)存在,
0.25t+20.5=88,
解得:t=270,
故存在,当t=270min时,选择套餐A或B的费用相同.
(3)由(2)可知,当t=270min时,两种套餐计费一样,
当t<270min时,选择套餐A,
当t>270min时,选择套餐B.
【解析】(1)根据t的范围进行分情况讨论;
(2)根据已知条件列出0.25t+20.5=88,解得t的值即可;
(3)由(2)可知,分情况分析.
本题主要考查一次函数的应用,数形结合是解题的关键.
23.【答案】(1)①证明:∵△ABC和△DEC都是等边三角形,
∴BC=AC,DC=CE,∠ACB=∠DCE=60∘=∠ABC,
∴∠BCD=∠ACE,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠ABC=60∘,
∴∠CAE=∠ACB=60∘,
∴AE//BC;
②解:如图2,取AB的中点H,连接FH,
∵△ABC和△DEC都是等边三角形,
∴BC=AC,DC=CE,∠ACB=∠DCE=60∘=∠ABC,
∴∠BCD=∠ACE,∠DBC=120∘,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠DBC=120∘,BD=AE,
∴∠BAE=60∘,
∵点F是BE的中点,点H是AB的中点,
∴FH=12AE,FH//AE,
∴∠EAB=∠FHB=60∘,
∵点H是AB的中点,点G是AD的中点,
∴AH=12AB,AG=12AD=12(AB+BD),
∴GH=AG−AH=12(AB+BD)−12AB=12BD,
∴FH=GH,
∴△FGH是等边三角形,
∴FG=FH=12AE,
∴FGAE=12;
(2)解:如图3,延长AC至F,使AD=CF,连接EF,
∵△ABC和△EDC都是等腰直角三角形,
∴∠BAC=∠DEC=90∘=∠DAC,DE=CE,AB=AC,
∴∠ADE+∠ACE=180∘,
又∵∠ACE+∠ECF=180∘,
∴∠ECF=∠ADE,
又∵AD=CF,
∴△ADE≌△FCE(SAS),
∴∠AED=∠FEC,AE=EF,
∴∠AEF=∠DEC=90∘,
∴∠EAF=45∘=∠ACB,
∴AE//BC,
∴点E在过点A平行于BC的直线上运动,
∴当CE⊥AE时,CE有最小值,
此时如图4,点D与点A重合,
设CE=x=DE,则AC= 2x,
∴BC= 2AC=2x,
∵∠BCE=∠ACB+∠ACE=90∘,
∴BE= BC2+CE2= 4x2+x2= 5x,
∴CEBE=x 5x= 55.
【解析】(1)①由“SAS”可证△ACE≌△BCD,可得∠CAE=∠ABC=60∘=∠ACB,可证AE//BC;
②由“SAS”可证△ACE≌△BCD,可得∠CAE=∠DBC=120∘,BD=AE,由三角形中位线定理可得FH=12AE,FH//AE,可证△FGH是等边三角形,可得FG=FH=12AE,即可求解;
(2)由“SAS”可证△ADE≌△FCE,可得∠AED=∠FEC,AE=EF,可求∠EAF=45∘=∠ACB,可得AE//BC,则点E在过点A平行于BC的直线上运动,即当CE⊥AE时,CE有最小值,设CE=x=DE,则AC= 2x,由勾股定理可求BE的长,即可求解.
本题是四边形综合题,考查了全等三角形的判定和性质,等边三角形的判定和性质,三角形中位线定理等知识,添加恰当辅助线构造全等三角形是解题的关键.
24.【答案】解:(1)直线m:y=12x+1交x,y轴于A,B,则点A、B的坐标分别为:(−2,0)、(0,1),
则AB= 1+22= 5;
(2)∵∠APB=45∘,且AB=BP,
则△ABP为直角三角形,则PB⊥AB,
而直线AB的表达式为:y=12x+1,
则直线PB的表达式为:y=−2x+1,
设点P(m,−2m+1),
∵AB=BP,
即12+22=m2+(−2m+1−1)2,
解得:m=1,
即点P(1,−1),
将点P的坐标代入y=kx+2k得:−1=k+2k,
解得:k=−13,
故直线的表达式为:y=−13x−23;
(3)设点E(m,−2m+2),点F(4,n),
过点E作直线HG交y轴于点G,交过点F和y轴的平行线于点H,
∵△DEF为等腰直角三角形,且∠DEF=90∘,则ED=EF,
∵∠DEG+∠FEH=90∘,∠FEH+∠EFH=90∘,
∴∠DEG=∠EFH,
∵∠EGD=∠FHE=90∘,
∴△EGD≌△FHE(AAS),
则DG=|−3+2m−2|=EH=4−m且GE=m=FH=|n+2m−2|,
解得:m=3或1,
即点E(3,−4)或(1,0).
【解析】(1)直线m:y=12x+1交x,y轴于A,B,则点A、B的坐标分别为:(−2,0)、(0,1),即可求解;
(2)∠APB=45∘,且AB=BP,则PB⊥AB,得到直线PB的表达式为:y=−2x+1,设点P(m,−2m+1),由AB=BP,即可求解;
(3)证明△EGD≌△FHE(AAS),则DG=|−3+2m−2|=EH=4−m且GE=m=FH=|n+2m−2|,即可求解.
本题考查的是一次函数的综合运用,涉及到三角形全等、直角三角形的性质等,分类求解是解题的关键.平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
30
60
81
50
40
110
130
146
90
100
60
31
120
140
70
81
10
20
100
81
课外阅读时间x(min)
0≤x<40
40≤x<80
80≤x<120
120≤x≤160
人数
a
5
7
4
平均数
中位数
众数
77.5
m
n
计费方式(元)
月使用费用(元)
主叫限定时间(分钟)
主叫超时费用(元/分钟)
被叫费用(元)
套餐A
58
150
0.25
0
套餐B
88
350
0.19
0
2023-2024学年湖北省武汉市汉阳区八年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年湖北省武汉市汉阳区八年级(下)期末数学试卷(含详细答案解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年湖北省武汉市东湖高新区八年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年湖北省武汉市东湖高新区八年级(下)期末数学试卷(含详细答案解析),共24页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。
2023-2024学年湖北省武汉市汉阳区七年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年湖北省武汉市汉阳区七年级(下)期末数学试卷(含详细答案解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












