2025高考数学一轮复习-3.2-导数与函数的单调性【课件】

这是一份2025高考数学一轮复习-3.2-导数与函数的单调性【课件】，共60页。PPT课件主要包含了知识诊断基础夯实，单调递增，单调递减，常数函数，定义域，得x≤－a或x≥a，考点突破题型剖析，角度1比较大小，ACD，角度2解不等式等内容，欢迎下载使用。

ZHISHIZHENDUANJICHUHANGSHI
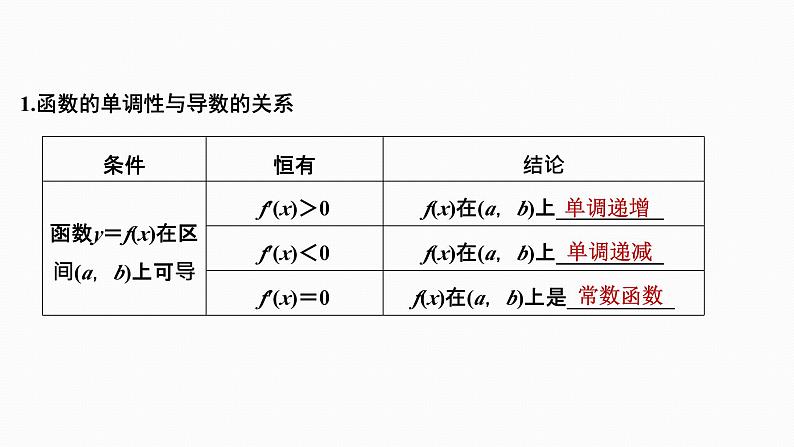
1.函数的单调性与导数的关系
第1步，确定函数的________；第2步，求出导函数f′(x)的______；第3步，用f′(x)的零点将f(x)的定义域划分为若干个区间，列表给出f′(x)在各区间上的正负，由此得出函数y＝f(x)在定义域内的单调性.
2.利用导数判断函数单调性的步骤
1.若函数f(x)在区间(a，b)上递增，则f′(x)≥0，所以“f′(x)>0在(a，b)上成立”是“f(x)在(a，b)上单调递增”的充分不必要条件.2.对于可导函数f(x)，“f′(x0)＝0”是“函数f(x)在x＝x0处有极值”的必要不充分条件.
解析　(1)f(x)在(a，b)内单调递增，则有f′(x)≥0.
1.思考辨析(在括号内打“√”或“×”)(1)函数f(x)在(a，b)内单调递增，那么一定有f′(x)＞0.(　　)(2)如果f(x)在某个区间内恒有f′(x)＝0，则f(x)在此区间内没有单调性.(　　)(3)若函数f(x)在定义域上都有f′(x)＞0，则f(x)在定义域上一定单调递增.(　　)(4)函数f(x)＝x－sin x在R上是增函数.(　　)
解析　由题意得，当x∈(－∞，c)时，f′(x)＞0，所以函数f(x)在(－∞，c)上是增函数，因为a＜b＜c，所以f(c)＞f(b)＞f(a).当x∈(c，e)时，f′(x)＜0，所以函数f(x)在(c，e)上是减函数，因为c＜d＜e，所以f(c)＞f(d)＞f(e).
2.(多选)已知定义在R上的函数f(x)，其导函数f′(x)的大致图象如图所示，则下列叙述正确的是(　　)A.f(b)＞f(c)＞f(d)B.f(b)＞f(a)＞f(e)C.f(c)＞f(b)＞f(a)D.f(c)＞f(d)＞f(e)
解析　由题意可得函数的定义域为(0，＋∞)，∵f(x)＝ln x－x2，
3.函数f(x)＝ln x－x2的单调递增区间为______________.
由f′(x)＞0可得1－2x2＞0，
解析　f′(x)＝3ax2＋6x－1，
4.若函数f(x)＝ax3＋3x2－x恰好有三个单调区间，则实数a的取值范围是____________________.
(－3，0)∪(0，＋∞)
解析　f′(x)＝x2－3x＋a，且f(x)的单调递减区间为[－1，4]，∴f′(x)＝x2－3x＋a≤0的解集为[－1，4], ∴－1，4是方程f′(x)＝0的两根，则a＝(－1)×4＝－4.
∵函数在[2，＋∞)上单调递增，∴[2，＋∞)⊆[a，＋∞)，∴a≤2.又a＞0，∴0＜a≤2.
在x∈[2，＋∞)上恒成立，即a2≤x2恒成立，∵x∈[2，＋∞)，∴x2≥4，∴a2≤4，又a＞0，∴0＜a≤2.
KAODIANTUPOTIXINGPOUXI
对于B，f′(x)＝(x＋1)ex＞0，符合题意；
1.下列函数中，在(0，＋∞)内为增函数的是(　　)A.f(x)＝sin 2x B.f(x)＝xexC.f(x)＝x3－x D.f(x)＝－x＋ln x
解析　∵函数f(x)＝2x2－ln x，
2.函数f(x)＝2x2－ln x的单调递减区间是(　　)
解析　f′(x)＝sin x＋xcs x－sin x＝xcs x.令f′(x)＝xcs x>0，则其在区间(－π，π)上的解集为
3.已知定义在区间(－π，π)上的函数f(x)＝xsin x＋cs x，则f(x)的递增区间是________________.
解　函数f(x)的定义域为(0，＋∞)，
∴f′(x)≥0在(0，＋∞)上恒成立，∴函数f(x)在(0，＋∞)上单调递增；
当a＝1时，函数f(x)在(0，＋∞)上单调递增；
解　f(x)的定义域为(0，＋∞)，
令x2－ax＋1＝0，Δ＝a2－4，
(ⅰ)当Δ≤0，即0＜a≤2时，f′(x)≤0，f(x)在(0，＋∞)上是减函数.故a≤2时，f(x)在(0，＋∞)上是减函数.(ⅱ)当Δ＞0，即a＞2时，令f′(x)＝0，得
∵函数g(x)在[1，2]上单调递增，∴g′(x)≥0在[1，2]上恒成立，
∴a≥－2x2－x在[1，2]上恒成立，∴a≥(－2x2－x)max，x∈[1，2].在[1，2]上，(－2x2－x)max＝－3，所以a≥－3.∴实数a的取值范围是[－3，＋∞).
(2)若g(x)在区间[1，2]上存在单调递增区间，求实数a的取值范围.解　g(x)在[1，2]上存在单调递增区间，则g′(x)＞0在[1，2]上有解，即a＞－2x2－x在[1，2]上有解，∴a＞(－2x2－x)min，又(－2x2－x)min＝－10，∴a＞－10.
∴当x∈[1，2]时，a≤－2x2－x恒成立，
迁移 (1)(变条件)若函数g(x)在区间[1，2]上单调递减，求实数a的取值范围.
∴当x＝2时，t＝－2x2－x取得最小值－10.所以a≤－10，即实数a的取值范围为(－∞，－10].
(2)(变条件)若函数g(x)在区间[1，2]上不单调，求实数a的取值范围.解　∵函数g(x)在区间[1，2]上不单调，∴g′(x)＝0在区间(1，2)内有解，
易知该函数在(1，2)上是减函数，∴y＝－2x2－x的值域为(－10，－3)，因此实数a的取值范围为(－10，－3).
由f(x)在R上单调递增，则f′(x)≥0在R上恒成立.令t＝cs x，t∈[－1，1]，
在t∈[－1，1]上恒成立.∴4t2－3at－5≤0在t∈[－1，1]上恒成立.令g(t)＝4t2－3at－5，
例3 (多选)(2021·淄博二模)已知e是自然对数的底数，则下列不等关系中不正确的是(　 　)
当0＜x＜e时，g′(x)＞0，当x＞e时，g′(x)＜0，所以g(x)在(0，e)上单调递增，在(e，＋∞)上单调递减.
∵e＜3＜π，∴g(e)＞g(3)＞g(π)，
解析　因为f(x)(x∈R)为奇函数，f(－1)＝0，所以f(1)＝－f(－1)＝0.
例4 设函数f′(x)是奇函数f(x)(x∈R)的导函数，f(－1)＝0，当x＞0时，xf′(x)－f(x)＜0，则使得f(x)＞0成立的x的取值范围是______________________.
(－∞，－1)∪(0，1)
则g(x)为偶函数，g(1)＝g(－1)＝0.
故g(x)在(0，＋∞)上单减，在(－∞，0)上单增.
综上知，使得f(x)＞0成立的x的取值范围是(－∞，－1)∪(0，1).
在(－∞，0)上，当x＜－1时，
解析　f′(x)g(x)＋f(x)g′(x)＞0⇔[f(x)g(x)]′＞0，所以函数y＝f(x)g(x)在(－∞，0)上单调递增.又由题意知函数y＝f(x)g(x)为奇函数，所以其图象关于原点对称，且过点(－3，0)，(3，0).数形结合可求得不等式f(x)g(x)＜0的解集为(－∞，－3)∪(0，3).
(2)设f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x＜0时，f′(x)g(x)＋f(x)g′(x)＞0，且g(－3)＝0，则不等式f(x)g(x)＜0的解集为__________________.
(－∞，－3)∪(0，3)
导数关系构造函数的一些常见结构1.对于不等式f′(x)＋g′(x)>0，构造函数F(x)＝f(x)＋g(x).2.对于不等式f′(x)－g′(x)>0，构造函数F(x)＝f(x)－g(x).特别地，对于不等式f′(x)>k，构造函数F(x)＝f(x)－kx.3.对于不等式f′(x)g(x)＋f(x)g′(x)>0，构造函数F(x)＝f(x)·g(x).
5.对于不等式xf′(x)＋nf(x)>0，构造函数F(x)＝xn·f(x).6.对于不等式f′(x)＋f(x)>0，构造函数F(x)＝ex·f(x).7.对于不等式f′(x)＋kf(x)>0，构造函数F(x)＝ekx·f(x).
∴g(x)在R上为增函数，又a＞0，
例1 f(x)为定义在R上的可导函数，且f′(x)＞f(x)，对任意正实数a，下列式子一定成立的是(　　)
一、利用f(x)与ex构造可导型函数
故f(a)＞eaf(0).
当x＞0时，xf′(x)－2f(x)＜0，可以推出当x＞0时，F′(x)＜0，F(x)在(0，＋∞)上单调递减.∵f(x)为偶函数，x2为偶函数，∴F(x)为偶函数，∴F(x)在(－∞，0)上单调递增.根据f(－1)＝0可得F(－1)＝0，根据函数的单调性、奇偶性可得函数图象(图略)，根据图象可知f(x)＞0的解集为(－1，0)∪(0，1).
例2 已知偶函数f(x)(x≠0)的导函数为f′(x)，且满足f(－1)＝0，当x＞0时，2f(x)＞xf′(x)，则使得f(x)＞0成立的x的取值范围是____________________.
(－1，0)∪(0，1)
二、利用f(x)与xn构造可导型函数
三、利用f(x)与sin x，cs x构造可导型函数
则f(ln x)＜f(ln y).又f(t)在(0，＋∞)上单调递增.则ln x＜ln y，∴1＜x＜y，即y－x＞0，所以ey－x＞e0＝1，A正确，B不正确；又y－x－1无法确定与0的关系，故C、D不正确.
FENCENGXUNLIAN GONGGUTISHENG
解析　利用导数与函数的单调性进行验证.f′(x)＞0的解集对应y＝f(x)的增区间，f′(x)＜0的解集对应y＝f(x)的减区间，验证只有D符合.
1.函数y＝f(x)的导函数y＝f′(x)的图象如图所示，则函数y＝f(x)的图象可能是(　　)
2.函数f(x)＝3＋xln x的单调递减区间是(　　)
解析　令g(x)＝f(x)－3x－6，则g′(x)＝f′(x)－3＜0，所以函数g(x)在R上单调递减，g(－2)＝f(－2)－3×(－2)－6＝0，由g(x)＜0⇔g(x)＜g(－2)，则x＞－2.
3.若函数f(x)的定义域为R，其导函数为f′(x).若f′(x)－3＜0恒成立，f(－2)＝0，则f(x)－3x＜6的解集为(　　)A.(－∞，－2) B.(－2，2)C.(－∞，2) D.(－2，＋∞)
令g(x)＝2ax2－4ax－1，则函数g(x)＝2ax2－4ax－1的对称轴方程为x＝1，若f(x)在(1，4)上不单调，则g(x)在区间(1，4)上有零点.
4.已知函数f(x)＝ax2－4ax－ln x，则f(x)在(1，4)上不单调的一个充分不必要条件可以是(　　)
当a＝0时，显然不成立；
A.b＜c＜a B.c＜a＜bC.a＜c＜b D.c＜b＜a
当0＜x＜e时，f′(x)＞0；当x＞e时，f′(x)＜0，则f(x)在(0，e)上单调递增，在(e，＋∞)上单调递减，
故f(a－1)＋f(2a2)≤0⇔f(a－1)≤f(－2a2)，
又当x＜0时，xf′(x)－f(x)＜0，所以g′(x)＜0，即函数g(x)在区间(－∞，0)内单调递减.因为f(x)为R上的偶函数，所以g(x)为(－∞，0)∪(0，＋∞)上的奇函数，所以函数g(x)在区间(0，＋∞)内单调递减.由0＜ln 2＜e＜3，可得g(3)＜g(e)＜g(ln 2)，即c＜a＜b.
解析　∵f(x)在[1，4]上单调递减，
解析　∵函数f(x)＝x2－ex－ax在R上存在单调递增区间，∴f′(x)＝2x－ex－a＞0，即a＜2x－ex有解.设g(x)＝2x－ex，则g′(x)＝2－ex，令g′(x)＝0，得x＝ln 2，则当x＜ln 2时，g′(x)＞0，g(x)单调递增，当x＞ln 2时，g′(x)＜0，g(x)单调递减，∴当x＝ln 2时，g(x)取得极大值也是最大值，且g(x)max＝g(ln 2)＝2ln 2－2，∴a＜2ln 2－2.
9.若函数f(x)＝x2－ex－ax在R上存在单调递增区间，则实数a的取值范围是__________________.
(－∞，2ln 2－2)
解　f′(x)＝(2x＋a)e－x－(x2＋ax＋b)·e－x＝[－x2＋(2－a)x＋a－b]e－x，∴f′(0)＝a－b，又f(0)＝b，∴f(x)在(0，f(0))处的切线方程为y－b＝(a－b)x，即(a－b)x－y＋b＝0，
10.函数f(x)＝(x2＋ax＋b)e－x，若f(x)在点(0，f(0))处的切线方程为6x－y－5＝0.(1)求a，b的值；
(2)求函数f(x)的单调区间.解　∵f(x)＝(x2＋x－5)e－x，x∈R，∴f′(x)＝(－x2＋x＋6)e－x＝－(x＋2)(x－3)e－x，当x＜－2或x＞3时，f′(x)＜0；当－2＜x＜3时，f′(x)＞0，故f(x)的单调递增区间是(－2，3)，单调递减区间是(－∞，－2)，(3，＋∞).
①当a≥1时，f′(x)＞0，故f(x)在(0，＋∞)上单调递增；②当a≤0时，f′(x)＜0，故f(x)在(0，＋∞)上单调递减；③当0＜a＜1时，令f′(x)＝0，
11.讨论函数f(x)＝(a－1)ln x＋ax2＋1的单调性.
综上，当a≥1时，f(x)在(0，＋∞)上单调递增；当a≤0时，f(x)在(0，＋∞)上单调递减；
当x∈(0，e)时，f′(x)＞0，f(x)单调递增；当x∈(e，＋∞)时，f′(x)＜0，f(x)单调递减，又f(a)＝f(2)＝f(4)＞f(b)＝f(16)，结合a，b∈(0，3)，所以b＜a＝2，又c＝＝lg0.3(0.2×0.3)＝lg0.30.2＋1＞1＋lg0.30.3＝2，所以b＜a＜c.
12.已知a，b∈(0，3)，且4ln a＝aln 4，4ln b＝bln 2，c＝，则(　　)A.c＜b＜a B.a＜c＜bC.b＜a＜c D.b＜c＜a
解析　由导函数的图象可知，导函数f′(x)的图象在x轴下方，即f′(x)＜0，故原函数为减函数，并且递减的速度是逐渐减慢.所以f(x)的示意图如图所示：
13.(多选)已知函数f(x)的定义域为R，其导函数f′(x)的图象如图所示，则对于任意的x1，x2∈R(x1≠x2)，下列结论正确的是(　　)
f(x)＜0恒成立，没有依据，故A不正确；B表示(x1－x2)与[f(x1)－f(x2)]异号，即f(x)为减函数，故B正确；C，D左边的式子意义为x1，x2中点对应的函数值，即图中点B的纵坐标值，右边式子代表的是函数值的平均值，即图中点A的纵坐标值，显然有左边小于右边，故C不正确，D正确.
当a＞0时，f(x)的递增区间为(0，1)，递减区间为(1，＋∞)；当a＜0时，f(x)的递增区间为(1，＋∞)，递减区间为(0，1)；当a＝0时，f(x)为常函数，无单调区间.
14.已知函数f(x)＝aln x－ax－3(a∈R).(1)求函数f(x)的单调区间；
即a＝－2，∴f(x)＝－2ln x＋2x－3，