广东省东莞市2023-2024学年七年级下学期期末数学试卷(含答案)

这是一份广东省东莞市2023-2024学年七年级下学期期末数学试卷(含答案)，共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．的相反数为( )
A.B.C.D.2
2．下列各点中,在第一象限的点是( )
A.B.C.D.
3．下列调查中,适合采用全面调查的是( )
A.了解我市中小学生上学所用的交通工具
B.了解“五一”假期来旗峰山游览的游客满意度
C.了解某校701班学生的视力情况
D.了解全国七年级学生的身高情况
4．如图,是一块梯形铁片的残余部分,量得,则的度数是( )
A.B.C.D.
5．若,下列各式错误的是( )
A.B.C.D.
6．能满足方程的一组解是( )
A.B.
C.D.
7．如图,直线与相交于点O,过O点作射线,下列选项中两个角是对顶角的是( )
A.与B.与C.与D.与
8．如图所示是中国象棋棋盘的一半.放置在平面直角坐标系中,若“相”的坐标为,D的坐标为,则“马”的坐标为( )
A.B.C.D.
9．已知x,y满足方程组,则无论m取何值,x,y恒有的关系式是( )
A.B.C.D.
10．已知关于x的方程的解大于0,则m的取值范围为( )
A.B.C.D.
二、填空题
11．计算：______.
12．2024年4月25日,神舟十八号载人飞船发射成功,神舟十八号将在太空“养鱼”,若想了解“鱼”生长的变化趋势,最适合的统计图是______(填“条形”“扇形”或“折线”)统计图.
13．已知,则代数式的值为______.
14．如图,直线a,b被直线c所截,则的同旁内角是______.
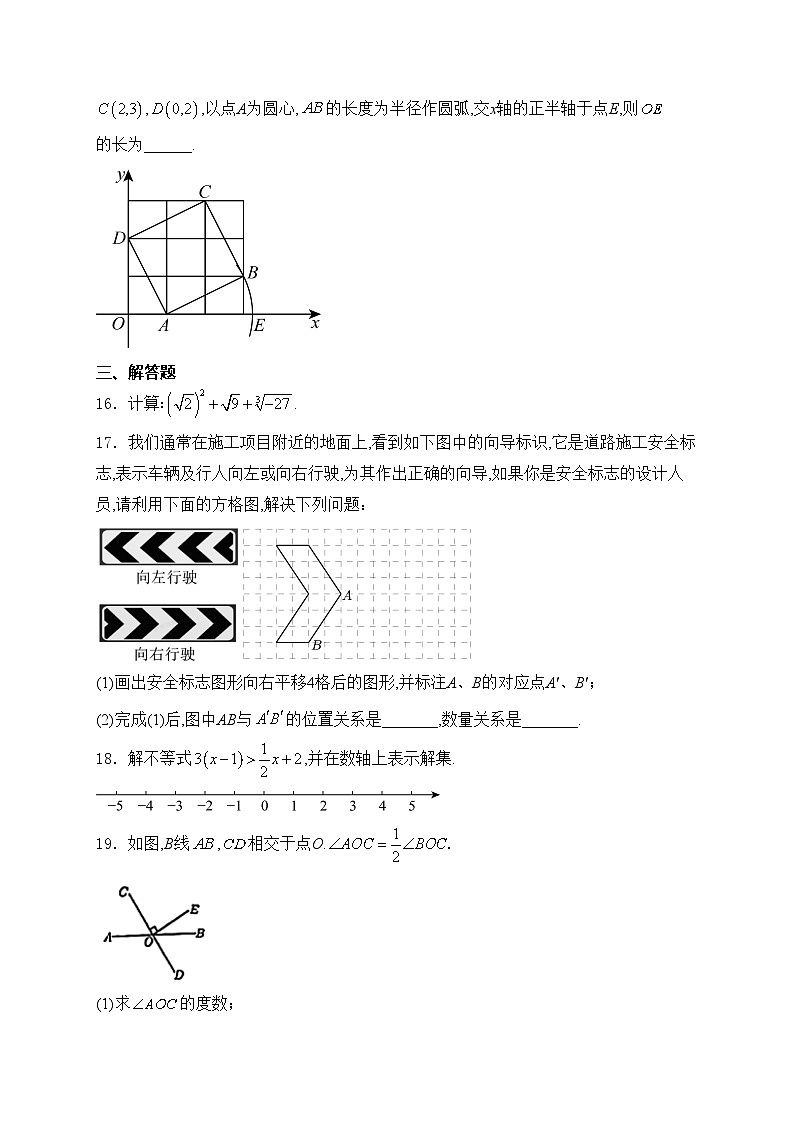
15．如图,平面直角坐标系中,正方形四个顶点的坐标分别是,,,,以点A为圆心,的长度为半径作圆弧,交x轴的正半轴于点E,则的长为______.
三、解答题
16．计算∶.
17．我们通常在施工项目附近的地面上,看到如下图中的向导标识,它是道路施工安全标志,表示车辆及行人向左或向右行驶,为其作出正确的向导,如果你是安全标志的设计人员,请利用下面的方格图,解决下列问题：
(1)画出安全标志图形向右平移4格后的图形,并标注A、B的对应点A'、B'；
(2)完成(1)后,图中AB与的位置关系是_______,数量关系是_______.
18．解不等式,并在数轴上表示解集.
19．如图,B线,相交于点O.
(1)求的度数；
(2)若,求的度数.
20．解方程组.
21．我市某校为了更好的开展劳动教育,采用随机抽样的方法,抽取了一部分学生,对他们一年前平均每月的劳动时间(单位：小时)进行了调查,将数据整理后绘制了如图不完整的频数分布直方面和扇形图.根据图中提供指出,解答下列问题：
(1)扇形形,______,E组对应的圆心角度数为度;
(2)这次抖音的样本容量是,补全频数分布直方图;
(3)请估计游技2000名学生中一年前平均每月的劳动时间不低于6小时的人数？
22．2024年5月5日,是中国羽毛球队的荣耀时刻,中国队时隔6年重新夺得代表羽毛球男子团体世界最高水平的汤姆斯杯、羽毛球运动消耗最大是羽毛球,为节约开支,羽毛球爱好者通常会购买2种羽毛球,即训练球和比赛球.若购买3桶训练球和2桶比赛球,共花费675元：购买3桶训练球的费用与购买1桶比赛球的费用相同.
(1)每桶羽毛球训练球和比赛球的价格各是多少元？
(2)若购买两种球共20桶,其中比赛球不少于6桶,所需费用总额不超过2800元,至少买训练球多少桶？请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方式
23．台球运动蕴含数学知识：台球桌面如1图是一个长方形,两组对边分别平行；台游直线运动：过台球与桌型碰撞的点作桌壁的垂线,该垂线平分台球碰撞前后运动所形成的天角.
(1)如2图,已知长方形桌面中,,一个球在桌面上的点A处滚向桌边,碰到上的点B后反弹,再碰到边上的点C后,再次反弹进入底袋点Q,在球碰到桌边反弹的过程中,,,都是直线,且,,,.求证：.
(2)如3图,若球在桌面的点A处,经过两次反弹后碰到边上的点D处,已站长方形桌面中,,.通过观察猜想与的位置关系,并证明你的猜想.
24．我国著名数学家华罗庚在杂志上看到这样的问题：求59319的立方根.他脱口而出：39.他是怎样快速准确算出来的呢？
(1)【知识储备】开立方与立方互为逆运算,如：因为,所以,因为,所以,因此,我们需要熟悉一些数及其立方.请补全表格：
(2)【思路探究】尝试求出19683的立方根是哪个整数：
①确定立方根的位数：由,猜想是______位数；
②确定个位的数字：根据(1)中各整数的立方的个位数字,确定的个位上的数字是______；
③确定十位的数字：由,且,确定的十位上的数字是______；
④确定立方根的值：由可得的值为______.
(3)【尝试应用】某商场拟建一个棱长为整数、容积为373248的正方体玻璃柜放置东莞迎思门(西城楼)模型,请问这个正方形棱长是多少？请写出求解过程.
25．综合探究:表示无理数整数部分与小数部分的思路：
,
,
的整数部分为2,小数部分为,
根据观察上述的规律后试解下面的问题：
(1)的整数部分为______,小数部分为______；
(2)已知其中a是是整数部分,b是小数部分.求的平方根；
(3)已知的小数部分为m,的小数部分为n,求关于x的不等式组的解集.
26．如图1,在平面直角坐标系中,点,,,且满足P点在线段上运动(不与O、A重合).
(1)直接写出点A的坐标,B的坐标,C的坐标；
(2)如图2,Q点在线段上运动,与的平分线交于点M,当时,点P在运动过程中,的大小是否变化？若不变,求出其值；若变化,说明理由：
(3)若点Q在y轴上运动(不与O、C重合),当与的角平分线交于点M时,根据点Q的运动位置,直接写出,和三者的数量关系.
参考答案
1．答案：B
解析：∵的相反数是,
故选：B.
2．答案：A
解析：因为第一象限内点的特征是,所以符合条件的选项只有,故选A.
3．答案：C
解析：A、了解我市中小学生上学所用的交通工具,适合采用抽样调查；故此选项不符合题意；
B、了解“五一”假期来旗峰山游览的游客满意度,适合采用抽样调查；故此选项不符合题意；
C、了解某校701班学生的视力情况,适合采用全面调查,故此选项符合题意；
D、了解全国七年级学生的身高情况,适合采用抽样调查；故此选项不符合题意；
故选：C.
4．答案：B
解析：∵上图是梯形铁片,
,
则,
则,
故选：B.
5．答案：A
解析：A、∵,∴,∴,故此选项符合题意；
B、∵,∴,故此选项不符合题意；
C、∵,∴,故此选项不符合题意；
D、∵,∴,故此选项不符合题意；
故选：A.
6．答案：D
解析：A、把代入方程左边,故此选项不符合题意；
B、把代入方程左边,故此选项不符合题意；
C、把代入方程左边,故此选项不符合题意；
D、把代入方程左边,故此选项符合题意；
故选：D.
7．答案：D
解析：A、与不是对顶角,故此选项不符合题意；
B、与不是对顶角,故此选项不符合题意；
C、与不是对顶角,故此选项不符合题意；
D、与是对顶角,故此选项符合题意；
故选：D.
8．答案：B
解析：“相”的坐标为,D的坐标为,可建立如图所示的平面直角坐标系：
所以“马”所在点的坐标为.
故选：B
9．答案：A
解析：
把②代入①,得,
∴,
故选：A.
10．答案：A
解析：
由题意,得
解得：
故选：A.
11．答案：4
解析：原式.
故答案为4.
12．答案：折线
解析：折线统计图,用点表示变化的数据,并且连接成线,能很好地反应数据变化情况.
因此想要了解“鱼”生长的变化趋势,应该选择的统计图是折线图.
故答案为：折线.
13．答案：
解析：,
∴
∴
故答案为：.
14．答案：
解析：与都在直线a、b之间,且它们都在直线c的同旁,
的同旁内角是.
故答案为：.
15．答案：
解析：正方形,
∴
∴
故答案为：.
16．答案：2
解析：原式
.
17．答案：(1)图见解析
(2)平行(或),相等(或)
解析：(1)图形如图所示：
(2),,
故答案为：,.
18．答案：,图见解析
解析：
在数轴上表示解集为：
.
19．答案：(1)
(2)
解析：(1),,
,
；
(2),
,
,,
,
.
20．答案：
解析：
得：,
解得：,
将代入①得：,
解得：,
将代入③得：,
解得：,
则方程组的解为.
21．答案：(1)40；14.4
(2)100；图见解析
(3)580人
解析：(1)本次调查的学生有：(人,
,
E组对应的圆心角度数为：,
故答案为：40,14.4；
(2)由(1)可知：这次抖音的样本容量是100；
D组的频数为：,
补全的频数分布直方图如图所示；
(3)(人,
答：该校2000名学生中每周的运动时间不少于6小时的约有580人.
22．答案：(1)每桶羽毛球训练球的价格是30元,比赛球的价格是20元；
(2)至少买训练球12桶,最省钱的购买方式为买训练球14桶,买比赛球6桶
解析：(1)设每桶羽毛球训练球的价格是a元,比赛球的价格是b元,
由题意得：,
解得：,
每桶羽毛球训练球的价格是75元,比赛球的价格是225元.
(2)设买训练球x桶,则买比赛球桶,根据题意,得
,
解得：,
∵x为整数,
∴至少买训练球12桶；
∴或13或14,
∴或7或6,
∴共有三种方案：方案一：买训练球12桶,则买比赛球8桶,所需费用总额为：(元)；
方案二：买训练球13桶,则买比赛球7桶,所需费用总额为：(元)；
方案三：买训练球14桶,则买比赛球6桶,所需费用总额为：(元)；
∵,
∴最省钱的购买方式为买训练球14桶,买比赛球6桶.
23．答案：(1)证明见解析
(2),理由见解析
解析：(1)∵,,,
∴,
∴,
∵,,
∴,即,
∴.
(2),
证明：∵,
∴,
由题意可知：,,
∴
∵,
∴,
∴.
24．答案：(1)64,125,343,512
(2)①两
②7
③2；
④27
(3)这个正方形棱长是72
解析：(1),,,,
故答案为：64,125,343,512；
(2)要得到的结果,可以按如下步骤思考：
①∵,,而,
∴,
由此得是两位数；
②∵19683的个位上的数是3,而只有7的立方的个位上的数是3,
∴的个位上的数是7；
③∵,,且,
所以的十位上的数字是2；
④综合以上可得,；
(3)设这个正方形棱长是x,
根据题意得：,
故,
求解如下：
第一步：确定的位数,因为,,而,所以,由此得是两位数；
第二步：确定个位数字,因为373248的个位上的数是8,而2的立方的个位上的数是8,所以的个位上的数是2；
第三步：确定十位数字,划去373248后面的三位248得到373,因为,,而,所以的十位上的数字是7；
综合以上可得,,
故这个正方形棱长是72.
25．答案：(1)3,
(2)
(3)
解析：(1),
,
的整数部分为3,小数部分为,
故答案为：3,；
(2),
,
的整数部分为15,小数部分为,
即,,
,
的平方根是；
(3),
,
,,
的小数部分为,的小数部分为,
即,,
化为,
解不等式得：,
解不等式得：,
此不等式组的解集为.
26．答案：(1)；；
(2)的大小没有变化,其值为
(3)当点Q在线段上时,；当点Q在延长线上时,；当点Q在延长线上时,
解析：(1)∵
∴,,
解得：,,
∴,,.
(2)过点M作,如图2,
∵
∴
∵,,
∴
∴
∴
∴
∵
∴
∴
∵与的平分线交于点M,
∴,,
∵
∴,
∵,,
∴
∴
∴
∴的大小没有变化,其值为.
(3)当点P在线段上时,过点M作,
∵与的平分线交于点M,
∴,,
∵
∴,
∵,,
∴
∴
∴
即；
当点P在延长线上时,过点M作,如图,
同理
即,
当点P在延长线上时,过点M作,如图,
同理,
即.
综上,当点P在线段上时,；当点P在延长线上时,；当点P在延长线上时,.
整数
1
2
3
4
5
6
7
8
9
10
100
整数的立方
1
8
27
216
729