吉林省长春市南关区2017届九年级(上)期中数学试卷(含解析)

这是一份吉林省长春市南关区2017届九年级(上)期中数学试卷(含解析)，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题（每小题3分，共24分）
1．下来式子中，属于最简二次根式的是（ ）
A． B． C． D．
2．下列运算中错误的是（ ）
A． += B．（﹣）2=3 C． = D．÷=2
3．若x1，x2是一元二次方程x2﹣3x﹣6=0的两个根，则x1+x2的值是（ ）
A．﹣3 B．3 C．﹣6 D．6
4．用配方法将方程x2﹣4x+2=0变形，正确的是（ ）
A．（x﹣2）2=0 B．（x﹣2）2=2 C．（x+2）2=0 D．（x+2）2=2
5．在Rt△ABC中，∠C=90°，若csB=，则tanA的值是（ ）
A． B． C． D．
6．如图，在菱形ABCD中，对角线AC与BD相交于点O，且AC=6，BD=8，则菱形ABCD的高AH的值是（ ）
A．4 B．5 C． D．
7．如图，在方格纸中，△ABC和△DPE的顶点均在格点上，要使△ABC∽△DPE，则点P所在的格点为（ ）
A．P1 B．P2 C．P3 D．P4
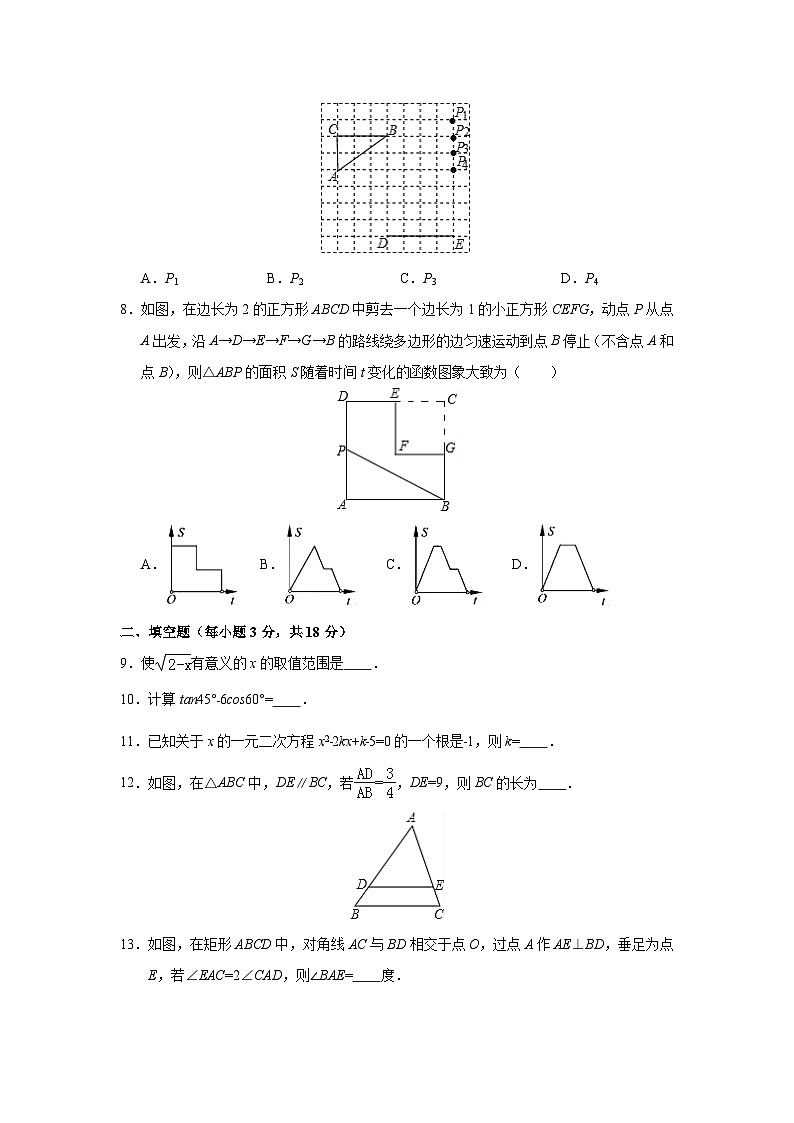
8．如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止（不含点A和点B），则△ABP的面积S随着时间t变化的函数图象大致为（ ）
A．B． C． D．
二、填空题（每小题3分，共18分）
9．使有意义的x的取值范围是 ．
10．计算tan45°﹣6cs60°= ．
11．已知关于x的一元二次方程x2﹣2kx+k﹣5=0的一个根是﹣1，则k= ．
12．如图，在△ABC中，DE∥BC，若=，DE=9，则BC的长为 ．
13．如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE= 度．
14．如图，直线l⊥x轴于点P，且与反比例函数y1=（x＞0）及y2=（x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为3，则k1﹣k2= ．
三、解答题（本大题共11小题，共78分）
15．计算：﹣3+．
16．解方程：x2+4x﹣1=0．
17．先化简，再求值：﹣，x=﹣1．
18．已知关于x的一元二次方程x2﹣（2k﹣1）x+k2﹣2k=0有实数根，求k的取值范围．
19．如图，在平面直角坐标系中，图中小正方形的边长均为1，已知△ABC三个顶点的坐标分别为A（﹣2，2），B（﹣4，0），C（﹣4，﹣4）．
（1）画出△ABC，以原点O为位似中心，将△ABC缩小为原来的，得到△A1B1C1；
（2）求∠A1C1B1的正弦值．
20．如图，一艘轮船位于灯塔P北偏东60°方向上，距离灯塔40海里的A处，它向西航行多少海里到达灯塔P北偏西45°方向上的B处．（参考数据：≈1.732，结果精确到0.1）
21．在国家政策的调控下，某市的商品房成交均价由今年5月份的每平方米10000元下降到7月份的每平方米8100元．
（1）求6、7两月平均每月降价的百分率；
（2）如果房价继续回落，按此降价的百分率，请你预测到9月份该市的商品房成交均价是否会跌破每平方米6500元？请说明理由．
22．如图，△ABC中，点D，E分别在边AB，AC上，∠ADE=∠C，∠BAC的平分线AG分别交线段DE，BC于点F，G．
（1）求证：△AEF∽△ABG；
（2）若=，求的值．
23．如图，在正方形ABCD中，点E，F分别是CB，BA延长线上的点，且BE=AF，连接DE，CF，CF交DE于点M，交AD于点H，过点E作EG⊥DE，使EG=DE，连接FG．
（1）求证：四边形GECF是平行四边形；
（2）若FA=2， =，求EG的长．
24．10月2日早晨8点，小华和同学骑自行车去净月潭游玩，当天按原路返回，如图，是小华出行的过程中，他距净月潭的距离y（千米）与他离开家的时间x（小时）之间的函数图象．
（1）小华去时骑自行车的速度是 ；
（2）求线段AB所表示的函数关系式；
（3）已知下午2点48分时，小华距净月潭12千米，求线段CD所表示的函数关系式，并求他何时到家．
25．如图，在平面直角坐标系中，直线y=mx+4与x，y轴分别交于A，B两点，直线y=﹣x+n与x，y轴分别交于C，D两点，点E（﹣，）是这两条直线的交点．
（1）求m，n的值；
（2）若点P是直线AB上一动点（不与点A重合），若△AOB与△ACP相似时，求点P的坐标．

2016-2017学年吉林省长春市南关区九年级（上）期中数学试卷
参考答案与试题解析

一、选择题（每小题3分，共24分）
1．下来式子中，属于最简二次根式的是（ ）
A．B．C．D．
【考点】最简二次根式．
【分析】结合最简二次根式的概念：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式．进行求解即可．
【解答】解：A、=2，不是最简二次根式，本选项不符合题意；
B、=3，不是最简二次根式，本选项不符合题意；
C、是最简二次根式，本选项符合题意；
D、=，不是最简二次根式，本选项不符合题意．
故选C．

2．下列运算中错误的是（ ）
A． +=B．（﹣）2=3C． =D．÷=2
【考点】二次根式的混合运算．
【分析】根据各个选项中的式子可以计算出正确的结果，从而可以判断哪个选项是错误的，本题得以解决．
【解答】解：∵不能合并，故选项A错误，
∵=3，故选项B正确，
∵，故选项C正确，
∵，故选项D正确，
故选A．

3．若x1，x2是一元二次方程x2﹣3x﹣6=0的两个根，则x1+x2的值是（ ）
A．﹣3B．3C．﹣6D．6
【考点】根与系数的关系．
【分析】根据一元二次方程根与系数的关系解答即可．
【解答】解：∵x1，x2是一元二次方程x2﹣3x﹣6=0的两个根，
∴x1+x2=3，
故选：B．

4．用配方法将方程x2﹣4x+2=0变形，正确的是（ ）
A．（x﹣2）2=0B．（x﹣2）2=2C．（x+2）2=0D．（x+2）2=2
【考点】解一元二次方程﹣配方法．
【分析】先把常数项移项，再方程两边同加上一次项系数一半的平方，再配方即可．
【解答】解：x2﹣4x+2=0，
移项得x2﹣4x=﹣2，
方程两边同加上4得，x2﹣4x+4=2，
配方得（x﹣2）2=2，
故选B．

5．在Rt△ABC中，∠C=90°，若csB=，则tanA的值是（ ）
A．B．C．D．
【考点】互余两角三角函数的关系．
【分析】根据一个角的正弦等于它余角的余弦，可得sin A，根据同角三角函数关系，可得答案．
【解答】解：由题意，得
sinA=csB=，
csA==，
tanA==，
故选：D．

6．如图，在菱形ABCD中，对角线AC与BD相交于点O，且AC=6，BD=8，则菱形ABCD的高AH的值是（ ）
A．4B．5C．D．
【考点】菱形的性质．
【分析】根据菱形的对角线互相垂直平分可得AC⊥BD，再求出OB、OC，然后利用勾股定理列式求出BC，然后根据菱形的面积等于对角线乘积的一半和底边乘以高两种方法列方程求解即可．
【解答】解：∵菱形ABCD，
∴AC⊥BD，
OB=BD=×8=4，
OC=AC=×6=3，
由勾股定理得，BC===5，
S菱形ABCD=AC•BD=BC•AH，
即×6×8=5AH，
解得AH=．
故选C．

7．如图，在方格纸中，△ABC和△DPE的顶点均在格点上，要使△ABC∽△DPE，则点P所在的格点为（ ）
A．P1B．P2C．P3D．P4
【考点】相似三角形的判定．
【分析】利用两个三角形都为直角三角形，则根据两组对应边的比相等且夹角对应相等的两个三角形相似，当=时，△ABC∽△DPE，然后利用比例性质计算出PE后可判断P点的位置．
【解答】解：∵∠DEP=∠ACB，
∴当=时，△ABC∽△DPE，
即=，
∴PE=6，
∴点P在格点P2的位置．
故选B．

8．如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止（不含点A和点B），则△ABP的面积S随着时间t变化的函数图象大致为（ ）
A．B．C．D．
【考点】动点问题的函数图象．
【分析】根据点P在AD、DE、EF、FG、GB上时，△ABP的面积S与时间t的关系确定函数图象．
【解答】解：当点P在AD上时，△ABP的底AB不变，高增大，所以△ABP的面积S随着时间t的增大而增大；
当点P在DE上时，△ABP的底AB不变，高不变，所以△ABP的面积S不变；
当点P在EF上时，△ABP的底AB不变，高减小，所以△ABP的面积S随着时间t的减小而减小；
当点P在FG上时，△ABP的底AB不变，高不变，所以△ABP的面积S不变；
当点P在GB上时，△ABP的底AB不变，高减小，所以△ABP的面积S随着时间t的减小而减小；
故选：C

二、填空题（每小题3分，共18分）
9．使有意义的x的取值范围是 x≤2 ．
【考点】二次根式有意义的条件．
【分析】根据二次根式的被开方数为非负数即可得出答案．
【解答】解：由题意得：2﹣x≥0，
解得：x≤2．
故答案为：x≤2．

10．计算tan45°﹣6cs60°= ﹣2 ．
【考点】特殊角的三角函数值．
【分析】根据特殊角的三角函数值，可得答案．
【解答】解：原式=1﹣6×=﹣2，
故答案为：﹣2．

11．已知关于x的一元二次方程x2﹣2kx+k﹣5=0的一个根是﹣1，则k= ．
【考点】一元二次方程的解．
【分析】把x=﹣1代入已知方程，列出关于k的新方程，通过解新方程可以求得k的值．
【解答】解：把x=﹣1代入方程x2﹣2kx+k﹣5=0，可得1+3k﹣5=0，即k=，
故答案是：．

12．如图，在△ABC中，DE∥BC，若=，DE=9，则BC的长为 12 ．
【考点】相似三角形的判定与性质．
【分析】根据DE∥BC，得到△ADE∽△ABC，得到==，即可求BC的长
【解答】解：DE∥BC，
则△ADE∽△ABC，
则==，
∵DE=9，
∴BC=12．
故答案为：12．

13．如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE= 22.5 度．
【考点】矩形的性质．
【分析】首先证明△AEO是等腰直角三角形，求出∠OAB，∠OAE即可．
【解答】解：∵四边形ABCD是矩形，
∴AC=BD，OA=OC，OB=OD，
∴OA=OB═OC，
∴∠OAD=∠ODA，∠OAB=∠OBA，
∴∠AOE=∠OAD+∠ODA=2∠OAD，
∵∠EAC=2∠CAD，
∴∠EAO=∠AOE，
∵AE⊥BD，
∴∠AEO=90°，
∴∠AOE=45°，
∴∠OAB=∠OBA==67.5°，
∴∠BAE=∠OAB﹣∠OAE=22.5°．
故答案为22.5°．

14．如图，直线l⊥x轴于点P，且与反比例函数y1=（x＞0）及y2=（x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为3，则k1﹣k2= 6 ．
【考点】反比例函数系数k的几何意义．
【分析】由反比例函数的图象过第一象限可得出k1＞0，k2＞0，再由反比例函数系数k的几何意义即可得出S△OAP=k1，S△OBP=k2，根据△OAB的面积为2结合三角形之间的关系即可得出结论．
【解答】解：∵反比例函数y1=（x＞0）及y2=（x＞0）的图象均在第一象限内，
∴k1＞0，k2＞0．
∵AP⊥x轴，
∴S△OAP=k1，S△OBP=k2．
∴S△OAB=S△OAP﹣S△OBP=（k1﹣k2）=3，
解得：k1﹣k2=6．
故答案为：6

三、解答题（本大题共11小题，共78分）
15．计算：﹣3+．
【考点】二次根式的加减法．
【分析】结合二次根式加减法的运算法则进行求解即可．
【解答】解：原式=2﹣+
=（2﹣+1）
=．

16．解方程：x2+4x﹣1=0．
【考点】解一元二次方程﹣配方法．
【分析】首先进行移项，得到x2+4x=1，方程左右两边同时加上4，则方程左边就是完全平方式，右边是常数的形式，再利用直接开平方法即可求解．
【解答】解：∵x2+4x﹣1=0
∴x2+4x=1
∴x2+4x+4=1+4
∴（x+2）2=5
∴x=﹣2±
∴x1=﹣2+，x2=﹣2﹣．

17．先化简，再求值：﹣，x=﹣1．
【考点】分式的化简求值．
【分析】根据分式的减法可以化简题目中的式子，然后将x的值代入化简后的式子即可解答本题．
【解答】解：﹣
=
=
=
=
=，
当x=﹣1时，原式==﹣1．

18．已知关于x的一元二次方程x2﹣（2k﹣1）x+k2﹣2k=0有实数根，求k的取值范围．
【考点】根的判别式．
【分析】根据方程有实数根得出△=[﹣（2k﹣1）]2﹣4×1×（k2﹣2k）=4k+1≥0，解之可得．
【解答】解：根据题意得△=[﹣（2k﹣1）]2﹣4×1×（k2﹣2k）=4k+1≥0，
解得：k≥﹣．

19．如图，在平面直角坐标系中，图中小正方形的边长均为1，已知△ABC三个顶点的坐标分别为A（﹣2，2），B（﹣4，0），C（﹣4，﹣4）．
（1）画出△ABC，以原点O为位似中心，将△ABC缩小为原来的，得到△A1B1C1；
（2）求∠A1C1B1的正弦值．
【考点】作图﹣位似变换；解直角三角形．
【分析】（1）利用相似图形的性质结合相似比进而得出对应点位置，即可得出答案；
（2）利用勾股定理得出各边长，再利用锐角三角函数关系求出答案．
【解答】解：（1）如图所示：△A1B1C1和△A2B2C2即为所求；
（2）如图所示：∵A1C1==，
∴sin∠A1C1B1==．

20．如图，一艘轮船位于灯塔P北偏东60°方向上，距离灯塔40海里的A处，它向西航行多少海里到达灯塔P北偏西45°方向上的B处．（参考数据：≈1.732，结果精确到0.1）
【考点】解直角三角形的应用﹣方向角问题．
【分析】过点P作PC⊥AB于点C，根据正弦、余弦的定义求出AC、PC，根据等腰直角三角形的性质求出BC，计算即可．
【解答】解：过点P作PC⊥AB于点C，
在Rt△APC中，PC=PA•cs60°=20，
AC=PC•sin60°=20，
在Rt△BPC中，∠BPC=45°，
∴BC=PC=20，
∴AB=BC+AC=20+20≈54.6（海里），
答：向西航行54.6海里到达灯塔P北偏西45°方向上的B处．

21．在国家政策的调控下，某市的商品房成交均价由今年5月份的每平方米10000元下降到7月份的每平方米8100元．
（1）求6、7两月平均每月降价的百分率；
（2）如果房价继续回落，按此降价的百分率，请你预测到9月份该市的商品房成交均价是否会跌破每平方米6500元？请说明理由．
【考点】一元二次方程的应用．
【分析】（1）根据每次的均价等于上一次的价格乘以（1﹣x）（x为平均每次下调的百分率），可列出一个一元二次方程，解此方程可得平均每次下调的百分率；
（2）求出9月份该市的商品房成交均价，即可判断．
【解答】（1）设6、7两月平均每月降价的百分率为x，根据题意得10000（1﹣x）2=8100，
即（1﹣x）2=0.81，解得x=10%或1.9（舍去）．
（2）∵8100（1﹣0.1）2=6561＞6500（元）．
∴不会跌破6500元．

22．如图，△ABC中，点D，E分别在边AB，AC上，∠ADE=∠C，∠BAC的平分线AG分别交线段DE，BC于点F，G．
（1）求证：△AEF∽△ABG；
（2）若=，求的值．
【考点】相似三角形的判定与性质．
【分析】（1）证明△ADE∽△ACB，得到∠B=∠AEF，根据角平分线的定义、相似三角形的判定定理证明；
（2）根据相似三角形的性质计算即可．
【解答】证明：（1）∵∠ADE=∠C，∠DAE=∠CAB，
∴△ADE∽△ACB，
∴∠B=∠AEF，
∵AG是∠BAC的平分线，
∴∠BAG=∠EAF，
∴△AEF∽△ABG；
（2）∵△AEF∽△ABG，
∴==，
∴=．

23．如图，在正方形ABCD中，点E，F分别是CB，BA延长线上的点，且BE=AF，连接DE，CF，CF交DE于点M，交AD于点H，过点E作EG⊥DE，使EG=DE，连接FG．
（1）求证：四边形GECF是平行四边形；
（2）若FA=2， =，求EG的长．
【考点】相似三角形的判定与性质；平行四边形的判定与性质；正方形的性质．
【分析】（1）证明△FBC≌△ECD，得到CF=BE，∠FCB=∠EDC，根据平行四边形的判定定理证明即可；
（2）根据相似三角形的性质列出比例式，计算即可．
【解答】（1）证明：∵AB=BC，BE=AF，
∴BF=CE，
在△FBC和△ECD中，
，
∴△FBC≌△ECD，
∴CF=BE，∠FCB=∠EDC，
∵EG=ED，
∴CF=EG，
∵∠DEC+∠EDC=90°，
∴∠DEC+∠FCB=90°，
∴CF⊥DE，
∵EG⊥DE，
∴CF∥EG，
∴四边形GECF是平行四边形；
（2）解：∵=，
∴=，
∵△FAH∽△CDH，
∴==，
∵FA=2，
∴CD=6，
∴CE=BF=FA+AB=8，
∴EG=DE==10．

24．10月2日早晨8点，小华和同学骑自行车去净月潭游玩，当天按原路返回，如图，是小华出行的过程中，他距净月潭的距离y（千米）与他离开家的时间x（小时）之间的函数图象．
（1）小华去时骑自行车的速度是 18千米/小时 ；
（2）求线段AB所表示的函数关系式；
（3）已知下午2点48分时，小华距净月潭12千米，求线段CD所表示的函数关系式，并求他何时到家．
【考点】一次函数的应用．
【分析】（1）根据速度=路程÷时间，代入数据即可得出结论；
（2）根据点A、B的坐标，利用待定系数法即可求出线段AB所表示的函数关系式；
（3）找出下午2点48分时的坐标，结合点C的坐标利用待定系数法即可求出线段CD所表示的函数关系式，再将y=18代入该关系式中求出x值，结合开始出发时的时间为8点即可得出结论．
【解答】解：（1）小华去骑自行车的速度18÷1=18（千米/小时）．
故答案为：18千米/小时．
（2）设线段AB所表示的函数关系式为y=kx+b（k≠0），
将A（0，18）、B（1，0）代入y=kx+b，
，解得：，
∴线段AB所表示的函数关系式为y=﹣18x+18（0≤x≤1）．
（3）由题意可知：下午2点48分时，即x=6.8，y=12．
设线段CD所表示的函数关系式y=mx+n（m≠0），
把（6.8，12）、（6，0）代入y=mx+n，
，解得：，
∴线段CD所表示的函数关系式为y=15x﹣90．
当y=18时，15x﹣90=18，
解得：x=7.2．
8时+7.2小时=15.2时=15时12分．
答：华15时12分到家．

25．如图，在平面直角坐标系中，直线y=mx+4与x，y轴分别交于A，B两点，直线y=﹣x+n与x，y轴分别交于C，D两点，点E（﹣，）是这两条直线的交点．
（1）求m，n的值；
（2）若点P是直线AB上一动点（不与点A重合），若△AOB与△ACP相似时，求点P的坐标．
【考点】一次函数综合题．
【分析】（1）把交点E的坐标分别代入两直线解析式即可求得m、n的值；
（2）由两直线解析式可分别求得A、B、C的坐标，可设出P点坐标，分别表示出AP、PC的长，且可求得AC、AO、BO的长，根据相似三角形的性质可得到关于P点坐标的方程，可求得P点坐标．
【解答】解：
（1）∵点E（﹣，）是直线y=mx+4和直线y=﹣x+n的交点，
∴=﹣m+4， =﹣×（﹣）+n，
解得m=2，n=1；
（2）由（1）可知直线AB解析式为y=2x+4，
令y=0可得2x+4=0，解得x=﹣2，令x=0可得y=4，
∴A（﹣2，0），B（0，4），
直线CD解析式为y=﹣x+1，
令y=0可得﹣x+1=0，解得x=3，
∴C（3，0），
∴AO=2，BO=4，AC=3﹣（﹣2）=5，AB==2，
∵P点在直线AB上，
∴可设P点坐标为（t，2t+4），
∵Rt△AOB与Rt△ACP相似，
∴有∠ACP=∠AOB=90°和∠AOB=∠APC=90°两种情况，
①当∠ACP=∠AOB=90°时，则可知t=3，代入直线AB解析式可得y=2×3+4=10，
∴P（3，10）；
②当∠APC=∠AOB=90°时，
∵△AOB∽△APC，
∴=，即=，
∴AP=，
∴=，解得t=﹣1或t=﹣3，当t=﹣3时，∠APC≠90°，舍去，
∴P（﹣1，2）；
综上可知，当△AOB与△ACP相似时，点P的坐标为P（3，10）或P（﹣1，2）．

2017年3月5日