

2023-2024学年贵州省贵阳市七年级(下)月考数学试卷(6月份)(含答案)
展开1.a2×a3的结果是( )
A. a6B. a5C. 2a6D. 2a5
2.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
3.手撕钢是一种超薄不锈精密带钢,具有良好的微观组织和性能.国产手撕钢的厚度仅有0.000015米,创造了新的世界纪录,广泛应用于航空航天、高端电子、新能源等.将数据0.000015用科学记数法表示为( )
A. 1.5×10−5B. 0.15×10−3C. 1.5×10−6D. 15×10−4
4.在△ABC中,∠A=30°,∠B=50°,那么△ABC形状是( )
A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形
5.如图,点O在直线BD上,已知∠1=25°,OC⊥OA,则∠BOC的度数为( )
A. 55°
B. 65°
C. 75°
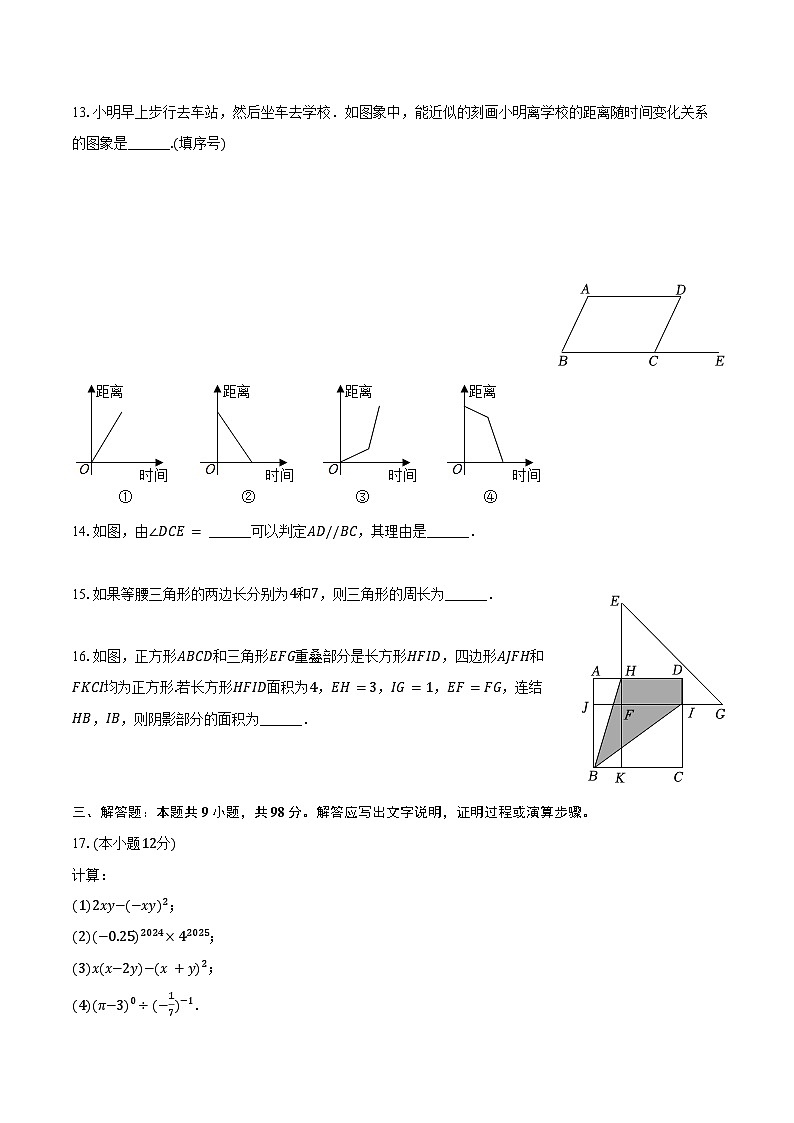
D. 155°
6.如图表,李师傅到小区附近的“爱心”加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A. 金额B. 数量C. 单价D. 金额和数量
7.在下列多项式的乘法中,不能用平方差公式的是( )
A. (x−3)(x+3)B. (x+3)(−x−3)
C. (−x+3)(−x−3)D. (x+3)(3−x)
8.如图,已知AD=AE,下列条件中,不能使△ADB≌△AEC的是( )
A. ∠B=∠C
B. ∠AEC=∠ADB
C. AB=AC
D. CE=BD
9.将一个直角三角尺和直尺按如图所示的方式摆放,直尺的一边经过点A,已知∠BAC=60°,若∠1=150°,则∠2的度数是( )
A. 30°
B. 40°
C. 45°
D. 50°
10.若x2+mx+16是一个完全平方式,则m的值为( )
A. ±8B. ±4C. 8D. 4
11.如图,点P在∠AOB内,线段MN交OA、OB于点E、F点,M、N分别是点P关于OA、OB的对称点,若△PEF的周长为15cm,则MN的长为( )
A. 10cmB. 12cmC. 15cmD. 18cm
12.如图,在△ABC中,延长CA至点F,使得AF=CA,延长AB至点D,使得BD=2AB,延长BC至点E,使得CE=3CB,连接EF、FD、DE,若S△DEF=36,则S△ABC为( )
A. 2B. 3C. 4D. 5
二、填空题:本题共4小题,每小题4分,共16分。
13.小明早上步行去车站,然后坐车去学校.如图象中,能近似的刻画小明离学校的距离随时间变化关系的图象是______.(填序号)
14.如图,由∠DCE= ______可以判定AD//BC,其理由是______.
15.如果等腰三角形的两边长分别为4和7,则三角形的周长为______.
16.如图,正方形ABCD和三角形EFG重叠部分是长方形HFID,四边形AJFH和FKCI均为正方形.若长方形HFID面积为4,EH=3,IG=1,EF=FG,连结HB,IB,则阴影部分的面积为______.
三、解答题:本题共9小题,共98分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题12分)
计算:
(1)2xy−(−xy)2;
(2)(−0.25)2024×42025;
(3)x(x−2y)−(x+y)2;
(4)(π−3)0÷(−17)−1.
18.(本小题10分)
学校有一块长方形的劳动教育基地,长3b米,宽2a米,后来为了满足需要,需在旁边开垦新的土地,使原来的长增加a米,宽增加b米.
(1)求该基地现在的土地面积是多少平方米?
(2)当a=3,b=2时,求增加的土地面积是多少平方米?
19.(本小题10分)
已知:∠α,∠β,线段c.求作:△ABC,使∠A=α,∠B=∠β,AB=c(不写作法,保留作图痕迹)
20.(本小题8分)
圆柱的底面半径为10cm,当圆柱的高变化时圆柱的体积也随之变化.
(1)在这个变化过程中,自变量是______,因变量是______;
(2)设圆柱的体积为V,圆柱的高为ℎ,则V与ℎ的关系式是______;
(3)当ℎ从1cm变化到10cm时,圆柱的体积如何变化?
21.(本小题10分)
在学习“利用三角形全等测距离”之后,七(1)班数学实践活动中,杨老师让同学们测量池塘A、B之间的距离(无法直接测量).小涵设计的方案是:如图,先在地上取一个可以直接到达A点的D点,取AD的中点C,连接BC并延长到E,使CB=CE,连接ED,则ED的长度即为AB的长度.
(1)你同意小涵的做法吗?并说明理由;
(2)若DE=20米,求池塘A、B之间的距离.
22.(本小题12分)
如图,在网格纸中每个小正方形的边长为1cm,请完成下列问题:
请在网格中画出△ABC关于直线n对称的△DEF;(其中,点A,B,C分别对应点D,E,F);若∠A=30°,∠C=45°,则∠E= ______°;求四边形ABFD的面积.
23.(本小题12分)
综合探究:某数学兴趣小组用“等面积法”构造了可以验证恒等式的图形:
(1)【探究】图中求阴影部分面积能够验证的恒等式是______;
(2)【应用】利用(1)中的结论计算:20242−2026×2022;
(3)【拓展】利用(1)中的结论计算:(2+1)(22+1)(24+1)(28+1)⋯(232+1).
24.(本小题12分)
问题情境
(1)如图①,已知∠B+∠E+∠D=360°,试探究直线AB与CD有怎样的位置关系?并说明理由.
小明给出下面正确的解法:
直线AB与CD的位置关系是AB//CD.
理由如下:
过点E作EF//AB(如图②所示),
所以∠B+∠BEF=180°(依据1),
因为∠B+∠BED+∠D=360°(已知),
所以∠B+∠BEF+∠FED+∠D=360°,
所以∠FED+∠D=180°,
所以EF//CD(依据2),
因为EF//AB,
所以AB//CD(依据3).
交流反思
上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?
“依据1”:______,
“依据2”:______,
“依据3”:______,
类比探究
(2)如图,当∠B、∠E、∠F、∠D满足条件______时,有AB//CD.
拓展延伸
(3)如图,当∠B、∠E、∠F、∠D满足条件______时,有AB//CD.
25.(本小题12分)
在△ABC中,小明利用尺规作了如图(1)所示的痕迹,已知AD=4,DE=2.
(1)观察图(1)中的尺规作图的痕迹,可以发现直线DF是线段AB的______,射线AE是∠DAC的______,小明作AE平分∠DAC的全等依据是______.
(2)在图(2)中,若EG⊥AC,EG=1,求△ADE的面积.
(3)若点P是直线DF上的一个动点,则AP+PE的最小值是______.
参考答案
1.B
2.A
3.A
4.C
5.B
6.C
7.B
8.D
9.A
10.A
11.C
12.A
13.④
14.∠D,内错角相等,两直线平行.
15.15或18
16.10
17.解:(1)原式=2xy−x2y2;
(2)原式=(−0.25)2024×42024×4
=(−0.25×4)2024×4
=(−1)2024×4
=1×4
=4;
(3)原式=x2−2xy−x2−2xy−y2
=−y2−4xy;
(4)原式=1÷(−7)
=−17.
18.解:(1)(3b+a)(2a+b)
=6ab+3b2+2a2+ab
=3b2+2a2+7ab(平方米),
答:该基地现在的土地面积是(3b2+2a+7ab)平方米.
(2)当a=3,b=2时,
该基地现在的土地面积为3b2+2a2+7ab=3×22+2×32+7×3×2=72(平方米),
原来基地的面积为2a×3b=6×3×2=36(平方米),
72−36=36(平方米),
答:增加的土地面积是36平方米.
19.解:如图所示:△ABC即为所求.
20.(1)圆柱的高,圆柱的体积.
(2)V=100πℎ.
(3)当ℎ=1时,V=100π;当ℎ=10时,V=1000π,
∴当ℎ从1cm变化到10cm时,圆柱的体积从100πcm3增大到1000πcm3.
21.解:(1)同意,理由如下:
∵点C是AD的中点,
∴AC=CD,
在△ACB与△DCE中,
AC=CD∠ACB=∠DCEBC=CE,
∴△ACB≌△DCE(SAS),
∴AB=DE;
(2)由(1)知,AB=DE,
∴池塘A、B之间的距离AB=DE=20米.
22.解:如图,△DEF为所作;
∵∠A=30°,∠C=45°,
∴∠B=180°−30°−45°=105°,
∵△ABC与△DEF关于直线n对称,
∴△ABC≌△DEF,
∴∠E=∠B=105°,
∴四边形ABFD的面积=12×(6+8)×4=28.
23.(1)a2−b2=(a+b)(a−b);
(2)原式=20242−(2024+2)(2024−2)
=20242−20242+4
=4;
(3)原式=(2−1)(2+1)(22+1)(24+1)(28+1)⋯(232+1)
=(22−1)(22+1)(24+1)(28+1)⋯(232+1)
=(24−1)(24+1)(28+1)⋯(232+1)
=(28−1)(28+1)⋯(232+1)
=(216−1)(216+1)⋯(232+1)
=(232−1)(232+1)
=264−1.
24.(1)两直线平行,同旁内角互补,同旁内角互补,两直线平行,
(2)如图,当∠B、∠BEF、∠EFD、∠D满足条件∠B+∠BEF+∠EFD+∠D=540°时,有AB//CD.
理由:过点E、F分别作GE//HF//CD.
则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,
∴∠GEF+∠EFD+∠FDC=360°;
又∵∠B+∠BEF+∠EFD+∠D=540°,
∴∠ABE+∠BEG=180°,
∴AB//GE,
∴AB//CD;
故答案为:∠B+∠BEF+∠EFD+∠D=540°;
(3)如图,当∠B、∠BEF、∠EFD、∠D满足条件∠B+∠BEF+∠EFD+∠D=540°时,有AB//CD.
理由:过点E、F分别作GE//HF//CD.
则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,
∴∠GEF+∠EFD+∠FDC=360°;
又∵∠B+∠BEF+∠EFD+∠D=540°,
∴∠ABE+∠BEG=180°,
∴AB//GE,
∴AB//CD,
故答案为:∠B+∠BEF+∠EFD+∠D=540°.
25.(1)线段AB的垂直平分线,∠DAC的平分线,SSS;
(2)过E作EH⊥AD于H,
∵AE是∠DAC的平分线,EG⊥AC,
∴EH=EG=1,
∴△ADE的面积=12AD⋅EH=12×4×1=2;
(3)6.
300.00
金额
44.248
数量/升
6.78
单价/元
2023-2024学年贵州省贵阳市清镇市七年级(下)期中数学试卷(含解析): 这是一份2023-2024学年贵州省贵阳市清镇市七年级(下)期中数学试卷(含解析),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年贵州省贵阳市七年级(下)期中数学试卷: 这是一份2022-2023学年贵州省贵阳市七年级(下)期中数学试卷,共16页。
贵州省贵阳市多区联考2023-2024学年七年级上学期期中数学试卷: 这是一份贵州省贵阳市多区联考2023-2024学年七年级上学期期中数学试卷,共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












