数学九年级上册4 探索三角形相似的条件备课ppt课件

这是一份数学九年级上册4 探索三角形相似的条件备课ppt课件，共23页。PPT课件主要包含了课前预习，成比例，典例讲练等内容，欢迎下载使用。
数学 九年级上册 BS版
1. 相似三角形的判定定理三.三边 的两个三角形相似.2. 利用三边成比例判定两个三角形相似的步骤.（1）排序：将三角形的三边按长短顺序排列.（2）计算：分别计算长、中、短三组边的比值.（3）判定：若三个比值相等，则相似；否则，不相似.
已知△ ABC 的三边长分别为8cm，10cm，12cm，△ DEF 的一边 长为4cm.若△ DEF 与△ ABC 相似，则△ DEF 的另外两边长可能 为（　C　）
【思路导航】两个三角形的三条边的长度都知道，就可以直接 使用“三边成比例的两个三角形相似”来进行判断求解.
【点拨】两个三角形的三边长都按大小排列，大比大、小比 小、中比中，看三个比值是否相等，若都相等，则两个三角形 相似；否则，不相似.
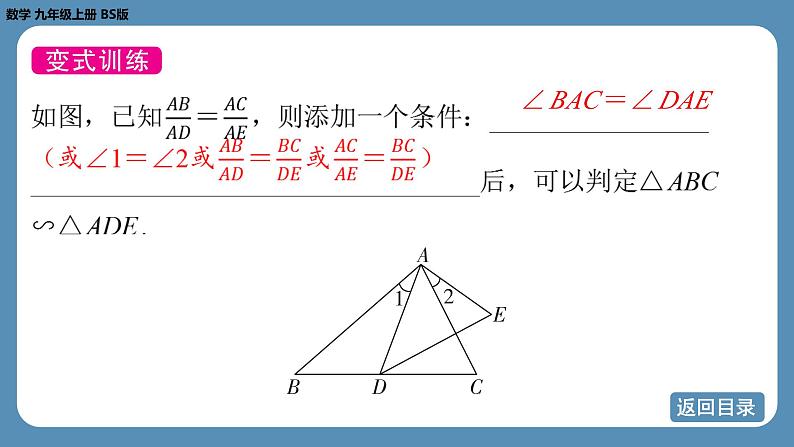
∠ BAC ＝∠ DAE
（1）∠ BAE 与∠ CAD 相等吗？为什么？（2）若∠ BAE ＝25°，求∠ DBC 的度数；
（3）试判断△ ABE 与△ ACD 是否相似，并说明理由.
【思路导航】（1）证明△ ABC ∽△ AED 即可得出结论；（2） 根据△ ABC ∽△ AED 和等量代换即可求出∠ DBC ；（3）利用 “两边成比例且夹角相等”即可证明.
（2）∵△ ABC ∽△ AED ， ∴∠ ABC ＝∠ AED . 又∵∠ ABC ＝∠ ABD ＋∠ DBC ， ∠ AED ＝∠ ABD ＋∠ BAE ，∴∠ DBC ＝∠ BAE ＝25°.
【点拨】当已知条件中（或经过探索后得到）两个三角形的某 两条边或三条边成比例时，可以考虑“三边成比例”或“两边 成比例且夹角相等”来判定这两个三角形相似.
如图，在△ ABC 中，已知 AB ＝25， BC ＝40， AC ＝20.在△ ADE 中， AE ＝12， AD ＝15， DE ＝24.求证：△ ADB ∽△ AEC .
如图，在边长为1的小正方形组成的网格中，△ ABC 和△ DEF 的顶点都在格点上，点 P1， P2， P3， P4， P5是△ DEF 边上的5 个格点，请按要求完成下列各题：
（1）试证明△ ABC 为直角三角形；
（2）判断△ DEF 和△ ABC 是否相似，并说明理由；
（3）直接写出一个与△ ABC 相似的三角形，使它的三个顶点为 点 P1， P2， P3， P4， P5中的三个格点.
【思路导航】（1）先求出△ ABC 各边的长度，再根据勾股定理 的逆定理判断即可；（2）先求出△ ABC 与△ DEF 各边的长 度，再根据“三边成比例的两个三角形相似”即可得出结论； （3）先求出各个边的长度，利用“三边成比例的两个三角形相 似”找到与△ ABC 相似的三角形.
（1）证明：由勾股定理，得 AB2＝22＋42＝20， AC2＝22＋12＝5， BC2＝32＋42＝25，∴ AB2＋ AC2＝ BC2.∴△ ABC 是直角三角形.
（3）解：与△ ABC 相似的三角形是△ P2 P4 P5.
【点拨】判断格点中的三角形是否相似，关键是看两个格点三 角形的三条对应边是否成比例.注意“对应关系”：大对大，中 对中，小对小.
如图，已知四边形 ABGH ， BCFG ， CDEF 都是边长为1的正方 形，连接 BH ， CH ， DH ，求证：∠ ABH ＋∠ ACH ＋∠ ADH ＝ 90°.