初中数学北师大版九年级上册4 探索三角形相似的条件教案配套ppt课件

这是一份初中数学北师大版九年级上册4 探索三角形相似的条件教案配套ppt课件，共25页。PPT课件主要包含了△HGR等内容，欢迎下载使用。
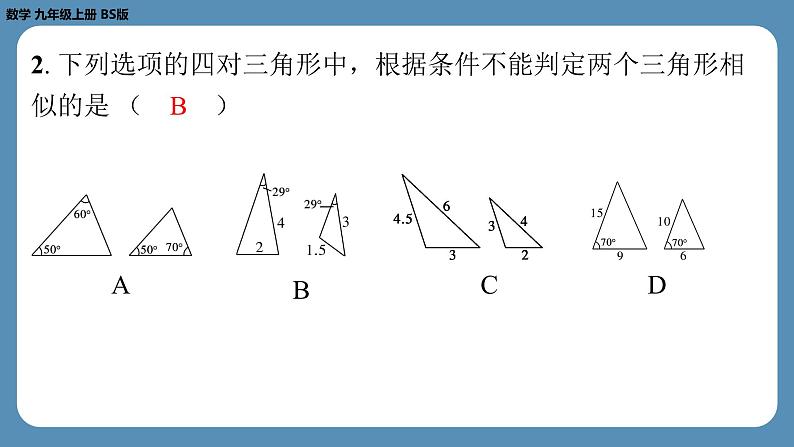
2. 下列选项的四对三角形中，根据条件不能判定两个三角形相 似的是 （　B　）
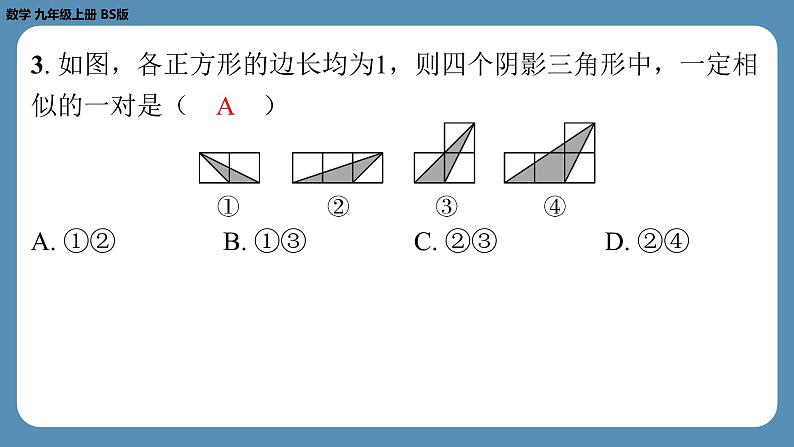
3. 如图，各正方形的边长均为1，则四个阴影三角形中，一定相 似的一对是（　A　）
4. 如图，在正方形网格中有3个三角形，则与△ FDE 相似的三角 形是 ⁠.
7. 如图，在△ ABC 中，已知点 D ， E ， F 分别是 AB ， BC ， CA 的中点.求证：△ EFD ∽△ ABC .
8. 如图，在平面直角坐标系中，已知点 A （3，0）， B （0， 4）， C （4，2），过点 C 作 CD ⊥ x 轴于点 D ，连接 AB ， BC ， AC . 求证：△ ABC ∽△ ACD .
证明：∵ A （3，0）， B （0，4），
∴ OA ＝3， OB ＝4.
∵ C （4，2）， CD ⊥ x 轴，
∴ OD ＝4， CD ＝2.
∴ AD ＝ OD － OA ＝1.
如答图，过点 C 作 CH ⊥ OB 于点 H .
则 OH ＝ CD ＝ BH ＝2， CH ＝ OD ＝4.
在△ ABC 和△ ACD 中，
∴△ ABC ∽△ ACD .
9. 如图，将三角形纸片（△ ABC ）折叠，使点 B 落在边 AC 上的 点 B '处，折痕为 EF ， AB ＝ AC ＝3， BC ＝4.若要使以点 B '， F ， C 为顶点的三角形与△ ABC 相似，则 BF 的长为 ⁠.
10. 如图，把一张3×4的方格纸放在平面直角坐标系内，每个方 格的边长为1个单位长度，△ ABC 的顶点都在方格的格点位置， 即点 A 的坐标是（1，0）.若点 D 也在格点位置（与点 A 不重 合），且使△ DBC 与△ ABC 相似，则符合条件的点 D 的坐标 是 ⁠.
（0，0），（3，2），（3，3）或（4，1）　
11. 如图，已知点 O 为△ ABC 内一点，点 A '， B '， C '分别是 OA ， OB ， OC 上的点，且 OA '∶ AA '＝ OB '∶ BB '＝1∶2， OC '∶ CC '＝2∶1，且 OB ＝6.（1）求证：△ OA ' B '∽△ OAB .
（1）证明：∵ OA '∶ AA '＝ OB '∶ BB '＝1∶2，∴ OA '∶ OA ＝ OB '∶ OB ＝1∶3.又∵∠ A ' OB '＝∠ AOB ，∴△ OA ' B '∽△ OAB .
（2）以点 O ， B '， C '为顶点的三角形是否可能与△ OBC 相 似？如果可能，求 OC 的长；如果不可能，请说明理由.
（2）解：可能相似.∵ OA '∶ AA '＝ OB '∶ BB '＝1∶2， OB ＝6，∴ OB '＝2.∵ OC '∶ CC '＝2∶1，∠ COB ＝∠ C ' OB '，∴可设 CC '＝ x ，则 OC '＝2 x ， OC ＝3 x .要使以点 O ， B '， C '为顶点的三角形与△ OBC 相似，
12. （选做）定义：若某个图形可分割为若干个都与它相似的图 形，则称这个图形是自相似图形.
探究：（1）如图1，在△ ABC 中，∠ C ＝90°，你能把△ ABC 分割成2 个与它自己相似的小直角三角形吗？若能，请在图1中画出分割 线，并说明理由.
解：（1）能.如图，过点 C 作 CD ⊥ AB 于点 D ， CD 即是满足要 求的分割线.理由如下：∵∠ B ＝∠ B ，∠ CDB ＝∠ ACB ＝90°，∴△ BCD ∽△ BAC . ∵∠ A ＝∠ A ，∠ ADC ＝∠ ACB ＝90°，∴△ ACD ∽△ ABC .
（2）一般地，“任意三角形都是自相似图形”，只要顺次连接 三角形各边中点，则可将原三分割为四个都与它自己相似的小 三角形.我们把△ DEF （图2）第一次顺次连接各边中点所进行 的分割，称为1阶分割（如图3）；把1阶分割得出的4个三角形 再分别顺次连接各边中点所进行的分割，称为2阶分割（如图 4）……依次规则操作下去. n 阶分割后得到的每一个小三角形都 是全等三角形（ n 为正整数），设此时小三角形的面积为 Sn .
②当 n ＞1时，请写出一个反映 Sn－1， Sn ， Sn＋1三者之间关系的 等式（不用证明）.