沪科版九年级上册22.4 图形的位似变换课堂教学ppt课件

这是一份沪科版九年级上册22.4 图形的位似变换课堂教学ppt课件，共29页。

1.(2024安徽安庆潜山期中)如图,在平面直角坐标系中,△ AOB和△COD是位似图形,点O是位似中心,CD=2AB.若点A 的坐标为(2,1),则点C的坐标为 (　    )A.(-6,-3)　　　B.(-5,-3)C.(-4,-2)　　　D.(-4,-3)
解析　∵△AOB和△COD是位似图形,点O是位似中心,CD= 2AB,点A的坐标为(2,1),∴点C的坐标为(-4,-2),故选C.
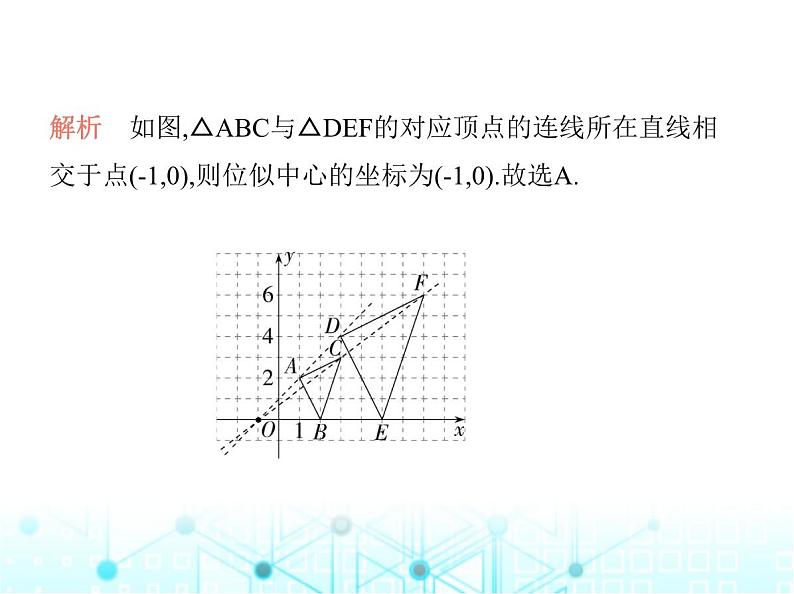
2.(2023四川遂宁中考)在方格图中,以格点为顶点的三角形 叫做格点三角形.在如图所示的平面直角坐标系中,格点△ ABC、△DEF成位似关系,则位似中心的坐标为 (　    )A.(-1,0)　　　B.(0,0)C.(0,1)　　　 D.(1,0)
解析　如图,△ABC与△DEF的对应顶点的连线所在直线相 交于点(-1,0),则位似中心的坐标为(-1,0).故选A. 
3.(易错题)(2023辽宁朝阳中考)如图,在平面直角坐标系中,已 知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB 放大,则点A的对应点A'的坐标是 (　    )A.(1,1)　　　B.(4,4)或(8,2)C.(4,4)　　　D.(4,4)或(-4,-4) 
解析　∵以原点O为位似中心,相似比为2,把△OAB放大,点 A的坐标为(2,2),∴点A的对应点A'的坐标为(2×2,2×2)或(2× (-2),2×(-2)),即(4,4)或(-4,-4),故选D.
4.如图,在平面直角坐标系中,△OAB与△OCD位似,位似中 心是坐标原点O,若点A(8,0),点C(4,0),则△OCD与△OAB面 积的比是　　    .
解析　∵A(8,0),C(4,0),∴OC∶OA=4∶8=1∶2.∵△OCD与 △OAB位似,位似中心是坐标原点O,∴相似比为1∶2,∴△OCD与△OAB面积的比是1∶4.
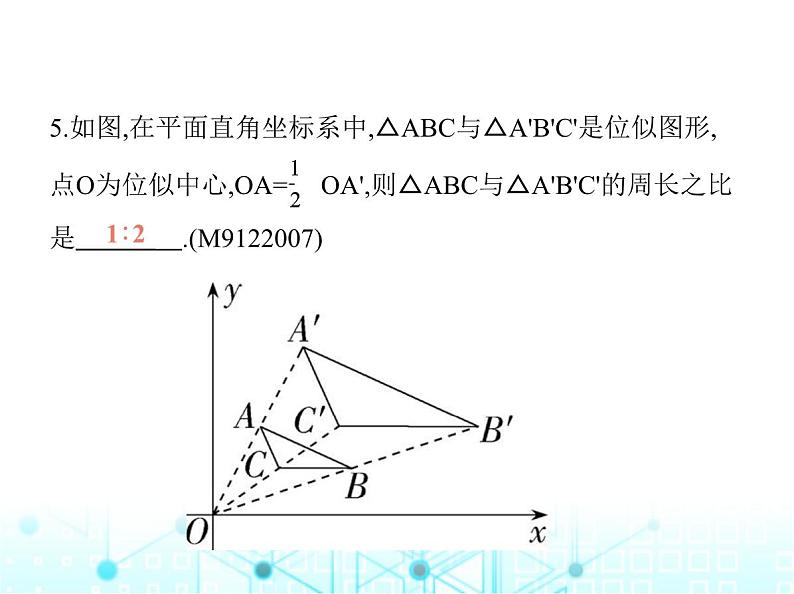
5.如图,在平面直角坐标系中,△ABC与△A'B'C'是位似图形, 点O为位似中心,OA= OA',则△ABC与△A'B'C'的周长之比是　　　    .(M9122007) 
解析    ∵OA= OA',∴ = .∵△ABC与△A'B'C'是位似图形,∴△ABC∽△A'B'C',AB∥A'B',∴△ABO∽△A'B'O,∴  = = ,∴△ABC与△A'B'C'的相似比是1∶2.∴△ABC与△A'B'C'的周长之比是1∶2.
6.(新独家原创)(新考法)如图,正方形OABC与正方形OA'B'C' 是以点O为位似中心的位似图形,相似比为1∶2,点A的坐标 为(0,1),则经过点B'的反比例函数图象的表达式为　　    .
解析　本题将位似和反比例函数图象综合起来进行考查,题 型新颖.∵正方形OABC与正方形OA'B'C'是位似图形,O为位似中心, 相似比为1∶2,∴OA∶OA'=1∶2.∵点A的坐标为(0,1),即OA=1,∴OA'=2.∵四边形OA'B'C'是正方形,∴A'B'=OA'=2.∴B'点的坐标为(2,2)或(-2,-2).设经过点B'的反比例函数图象 的表达式为y= ,将B'的坐标代入,得k=4,所以经过点B'的反
比例函数图象的表达式为y= .
7.(教材变式·P98T2)(2024安徽六安舒城期末)如图,在网格图 中(小正方形的边长为1),△ABC的三个顶点都在格点上.(M9 122007)(1)把△ABC沿着x轴向右平移6个单位得到△A1B1C1,请画出 △A1B1C1;(2)请以坐标系的原点O为位似中心在第一象限内画出△ ABC的位似图形△A2B2C2,使得△ABC与△A2B2C2的相似比 为1∶2;(3)请直接写出△A2B2C2三个顶点的坐标.
解析    (1)如图,△A1B1C1为所作.(2)如图,△A2B2C2为所作. (3)△A2B2C2三个顶点的坐标分别为A2(6,0),B2(6,4),C2(2,6).
8.(2024四川成都武侯期末,6, )如图,在平面直角坐标系xOy中,矩形OABC顶点的坐标分别是O(0,0),A(6,0),B(6,4),C (0,4).已知矩形OA'B'C'与矩形OABC位似,位似中心是原点O, 且矩形OA'B'C'的面积等于矩形OABC的面积的 ,则点B'的坐标是(M9122007)(　    )A.(3,2)　　　 B.(-3,-2)C.(3,2)或(-3,-2)　　　D.(2,3)或(-2,-3)
解析　∵矩形OA'B'C'与矩形OABC位似,矩形OA'B'C'的面 积等于矩形OABC面积的 ,∴矩形OA'B'C'与矩形OABC的相似比为1∶2,∵位似中心是原点O,B(6,4),∴点B'的坐标为 或 ,即(3,2)或(-3,-2),故选C.
9.(2023黑龙江绥化中考,19, )如图,在平面直角坐标系中,△ABC与△AB'C'的相似比为1∶2,点A是位似中心,已知 点A(2,0),点C(a,b),∠C=90°,则点C'的坐标为　　　    .(结果 用含a,b的式子表示)
 (6-2a,-2b)
解析　如图,过C作CM⊥AB于M,过C'作C'N⊥AB'于N, 则∠ANC'=∠AMC=90°,∵△ABC与△AB'C'的相似比为1∶ 2,∴ = .
∵∠NAC'=∠CAM,∠ANC'=∠AMC,∴△ACM∽△AC'N,∴ = = .∵点A(2,0),点C(a,b),∴OA=2,OM=a,CM=b,∴AM=a-2,∴  = = ,∴AN=2a-4,C'N=2b,∴ON=AN-OA=2a-6,∴点C'的坐标为(6-2a,-2b).
10.(2024安徽六安汇文中学期中,17, )如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C (3,5).(M9122007)(1)请画出△ABC关于x轴对称的△A1B1C1;(2)以O为位似中心,在第三象限内画出△ABC的位似图形△A2B2C2,且相似比为1;(3)借助网格,利用无刻度直尺画出线段CD,与AB交于点D,使 CD平分△ABC的面积.(保留确定点D的作图痕迹)
解析    (1)如图所示,△A1B1C1即为所求.(2)如图所示,△A2B2C2即为所求.(3)如图所示,CD即为所求. 
11.(几何直观)(新考向·规律探究题)如图,在平面直角坐标系 中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=1,
OC= ,在第二象限内,以原点O为位似中心将矩形AOCB放大为原来的 倍,得到矩形A1OC1B1,再以原点O为位似中心将矩形A1OC1B1放大为原来的 倍,得到矩形A2OC2B2,……,以此类推,得到的矩形A100OC100B100的对角线交点的纵坐标为　     　    .  
解析　∵OA=1,OC= ,∴点B的坐标为 ,∴矩形AOCB的对角线交点的坐标为 ,则矩形A1OC1B1的对角线交点的纵坐标为 × = = ,矩形A2OC2B2的对角线交点的纵坐标为 × = = ,∴矩形A100OC100B100的对角线交点的纵坐标为 .
12.(几何直观)(新考向·新定义试题)如果两个一次函数y=k1x +b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为 “平行一次函数”.如图,已知函数y=-2x+4的图象与x轴、y 轴分别交于A、B两点,一次函数y=kx+b与y=-2x+4是“平行 一次函数”.(1)若函数y=kx+b的图象过点(1,1),求b的值;(2)若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB 构成位似图形,位似中心为原点,相似比为1∶2,求函数y=kx+ b的表达式.
解析    (1)∵一次函数y=kx+b与y=-2x+4是“平行一次函 数”,∴k=-2.∵函数y=kx+b的图象过点(1,1),∴-2×1+b=1,解得b=3.(2)对于y=-2x+4,当x=0时,y=4,当y=0时,x=2,∴点A的坐标为(2,0),点B的坐标为(0,4),∵函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构 成位似图形,位似中心为原点,相似比为1∶2,∴点A的对应点的坐标为(1,0)或(-1,0),点B的对应点的坐标