
江西省赣州市于都县2023-2024学年七年级下学期4月期中考试数学试卷(含答案)
展开一、单选题
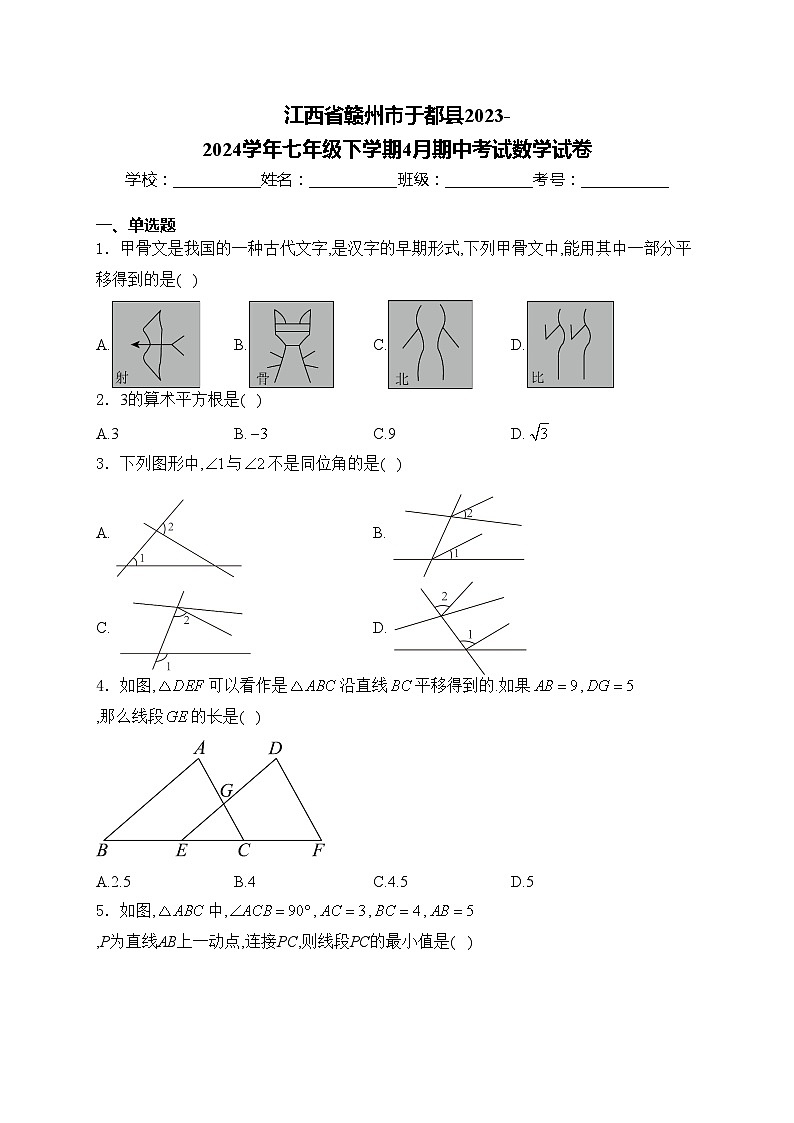
1.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )
A.B.C.D.
2.3的算术平方根是( )
A.3B.C.9D.
3.下列图形中,与不是同位角的是( )
A.B.
C.D.
4.如图,可以看作是沿直线平移得到的.如果,,那么线段的长是( )
A.2.5B.4C.4.5D.5
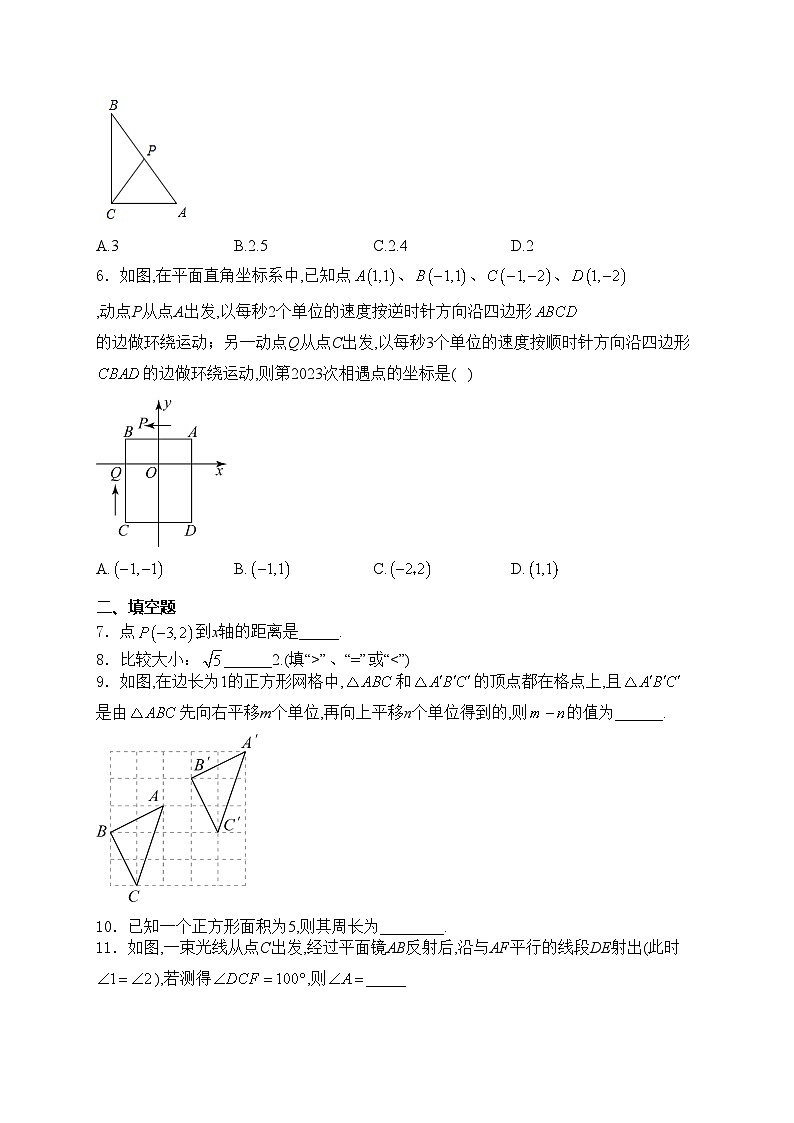
5.如图,中,,,,,P为直线AB上一动点,连接PC,则线段PC的最小值是( )
A.3B.2.5C.2.4D.2
6.如图,在平面直角坐标系中,已知点、、、,动点P从点A出发,以每秒2个单位的速度按逆时针方向沿四边形的边做环绕运动;另一动点Q从点C出发,以每秒3个单位的速度按顺时针方向沿四边形的边做环绕运动,则第2023次相遇点的坐标是( )
A.B.C.D.
二、填空题
7.点到x轴的距离是_____.
8.比较大小:______2.(填“>”、“=”或“<”)
9.如图,在边长为1的正方形网格中,和的顶点都在格点上,且是由先向右平移m个单位,再向上平移n个单位得到的,则的值为______.
10.已知一个正方形面积为5,则其周长为________.
11.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时),若测得,则_____
12.已知点,坐标轴,且,若点B在x轴的上方,则点B坐标为__.
三、解答题
13.如图,直线与相交于点F,于点F.
(1)图中与相等的角是_____,与互余的角是_____;
(2)若,求的度数.
14.计算:.
15.课堂上,老师让同学们从下列数中找一个无理数:
,,,0,,,
其中,甲说“”,乙说“”,丙说“”
(1)甲、乙、丙三个人中,说错的是________.
(2)请将老师所给的数字按要求填入下面相应的区域内;
16.如图是光明小区内的一幢商品房的示意图.若小李,小赵家所在的位置分别用,表示.
(1)用有序数对表示小张家的位置;
(2),分别表示谁家所在的位置?
17.完成下面推理过程:
已知:如图,已知,,.
求证:.
证明:,,,(已知)
__________.(在同一平面内,垂直于同一条直线的两条直线平行)
,(________________________)
又,,(已知)
________,(等量代换)
.(________________________)
18.在平面直角坐标系中,已知点,.
(1)若点B在x轴上,求点A的坐标;
(2)若线段轴,求a的值.
19.已知,如图,BC与DE相交于点O,给出下面三个论断:①;②;③.请以其中的两个论断为条件,填入“题设”栏中;剩下的论断为结论,填入“结论”栏中,使之成为一个真命题,并加以证明.
题设:已知:如图,BC与DE相交于点O,________,_______(填序号).
结论:__________(填序号).
20.如图图形,每个小正方形的边长为1.
(1)求图中阴影部分的面积和边长;
(2)已知x为阴影正方形边长的小数部分,y为的整数部分,求:
①x,y的值;
②的算术平方根.
21.小明制作了一张面积为的正方形贺卡想寄给朋友.现有一个长方形信封如图所示,长、宽之比为,面积为.
(1)求长方形信封的长和宽;
(2)小明能将贺卡不折叠就放入此信封吗?请通过计算给出判断.
22.如图,点A在x轴的负半轴上,点D在y轴的正半轴上,将三角形沿x轴向右平移,平移后得到三角形,点A的对应点是点B.已知点A的坐标为,点C的坐标为,且a,b,c满足.
(1)求点B的坐标.
(2)求证:.
23.问题背景观察小猪的主题,从中可以抽象出如图1所示的图形,
问题探究(1)如图1,,为、之间一点,连接、.可以得到与、之间有怎样的数量关系,并说明理由.
灵活应用(2)如图2,直线,若,,求的度数.
参考答案
1.答案:D
解析:A、是轴对称图形,不能用其中一部分平移得到,不符合题意;
B、是轴对称图形,不能用其中一部分平移得到,不符合题意;
C、是轴对称图形,不能用其中一部分平移得到,不符合题意;
D、能用其中一部分平移得到,符合题意;
故选D.
2.答案:D
解析:3的算术平方根是,
故选:D.
3.答案:B
解析:A,C,D中的与是同位角,
B中的与不是同位角,
故选:B.
4.答案:B
解析:∵由平移而成,
∴,
∵,
∴.
故选:B.
5.答案:C
解析:在中,,,,,
∵当时,PC的值最小,
此时:的面积,
∴,
∴,
故选:C.
6.答案:D
解析:∵点、、、,
∴,,
∴矩形的周长为,
由题意,经过1秒时,P、Q在点处相遇,接下来P、Q两点走的路程和是10的倍数时,两点相遇,相邻两次相遇间隔时间为秒,
∴第二次相遇点是的中点,
第三次相遇点是点,
第四次相遇点是点,
第五次相遇点是点,
第六次相遇点是点,……,
由此发现,每五次相遇点重合一次,
∵,
∴第2023次相遇点的坐标与第三次相遇点的坐标重合,即,
故选:D.
7.答案:2
解析:点到x轴的距离是.
故答案为:2.
8.答案:>
解析:∵,
∴,
∴,
故答案为:>.
9.答案:1
解析:是由向右平移3个单位,再向上平移2个单位得到的,
所以,,
则,
故答案为:1.
10.答案:
解析:∵正方形面积为5,
∴其边长为,
∴正方形的周长为.
故答案为:.
11.答案:50°
解析:∵,
∴,
∵,
∴,
∵,
∴,
故答案为:.
12.答案:或或
解析:①当轴时,∵,且,
∴点B坐标为或,又∵点B在x轴的上方,
∴点B的坐标为;
②当轴时,∵,且,∴点B坐标为或;
综上,点B坐标为或或,
故答案为:或或.
13.答案:(1),
(2)
解析:(1)∵和的对顶角,
∴,
∵,
∴,
即,
∴,
即与互余的角是,
故答案为:,;
(2)∵,
∴,
∵,
∴,
∴.
14.答案:
解析:
.
15.答案:(1)甲
(2)正实数为,,负分数为
解析:(1)是负分数,即是有理数范围内的,不是无理数,故甲错;
(2)正实数包括正有理数与正无理数,故答案为:、;
负分数为:.
16.答案:(1)
(2)表示小王家的位置;表示小周家的位置
解析:(1)小李,小赵家所在的位置分别用,表示,可找到原点如图所示:
根据图示,小张家的位置可用来表示
(2)根据上图示,表示小王家的位置;表示小周家的位置.
17.答案:见解析
解析:,,(已知)
.(在同一平面内,垂直于同一条直线的两条直线平行.)
.(两直线平行,同位角相等.)
又,(已知)
.(等量代换)
.(内错角相等,两直线平行.)
18.答案:(1)点
(2)
解析:(1)∵在x轴上,
∴,
∴,
∴,
∴点A坐标为;
(2)∵点,,线段轴,
∴,
∴.
19.答案:②,③;①;证明见解析
解析:题设:②、③
结论:①
证明:∵,
∴.
又∵,
∴.
∴.
20.答案:(1),
(2)①,
②
解析:(1)根据题意可得,
,
则阴影部分正方形的边长为:.
故答案为:13,;
(2)①,,
,,
,,
②∵,
,
即的算术平方根为.
21.答案:(1)长为,宽为
(2)小明能将这张贺卡不折叠就放入此信封,见解析
解析:(1)∵信封的长、宽之比为,
∴设长方形信封的长为,宽为,
由题意得,
∴(负值舍去),
∴长方形信封的长为,宽为;
(2)面积为的正方形贺卡的边长是.
∵,所以,
∴,即信封的宽大于正方形贺卡的边长,
∴小明能将这张贺卡不折叠就放入此信封.
22.答案:(1)
(2)证明见解析
解析:(1)∵,
∴,,,
解得,,,
∴,,,
则根据平移性质得,
∴;
(2)∵三角形沿x轴向右平移,平移后得到三角形,
∴,,
∴,,
∴.
23.答案:(1),理由见解析
(2)
解析:(1),
理由如下:点E作,如图1,
,
,
,,
,
;
(2),,
,
,
由(1)可得.
江西省赣州市于都县2023-2024学年八年级下学期期中考试数学试卷(含答案): 这是一份江西省赣州市于都县2023-2024学年八年级下学期期中考试数学试卷(含答案),共16页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
江西省赣州市于都县2023-2024学年七年级下学期4月期中考试数学试卷(含解析): 这是一份江西省赣州市于都县2023-2024学年七年级下学期4月期中考试数学试卷(含解析),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
江西省赣州市于都县2023-2024学年八年级下学期期中考试数学试卷(含解析): 这是一份江西省赣州市于都县2023-2024学年八年级下学期期中考试数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













