



还剩20页未读,
继续阅读
2024-2025学年度北师版八上数学-专题1-勾股定理及其逆定理在平面几何中的应用【课外培优课件】
展开
这是一份2024-2025学年度北师版八上数学-专题1-勾股定理及其逆定理在平面几何中的应用【课外培优课件】,共28页。
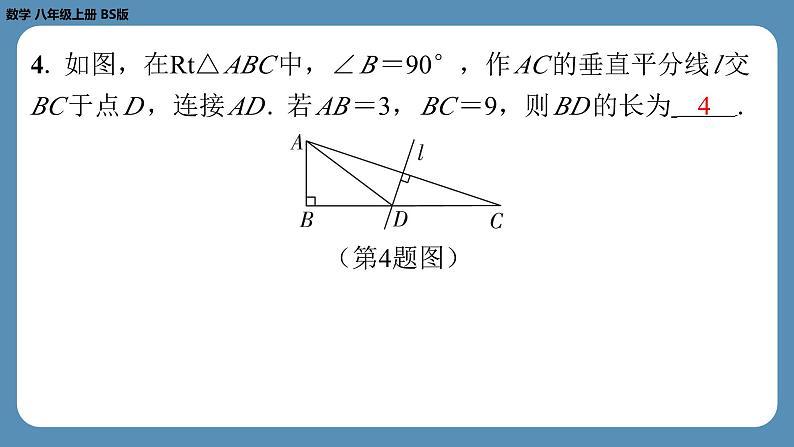
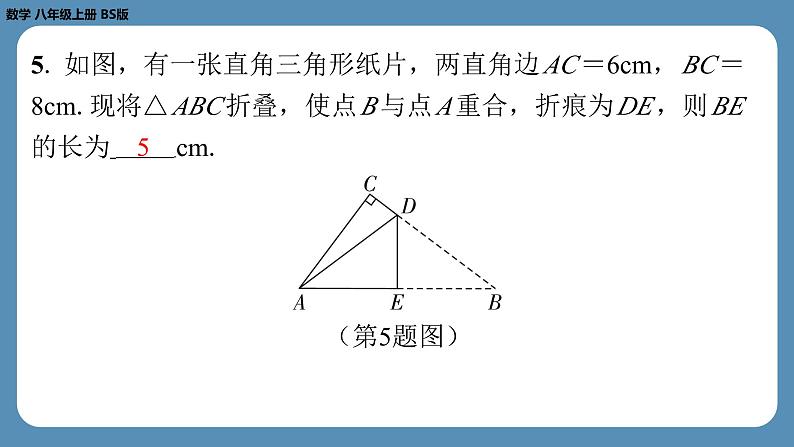
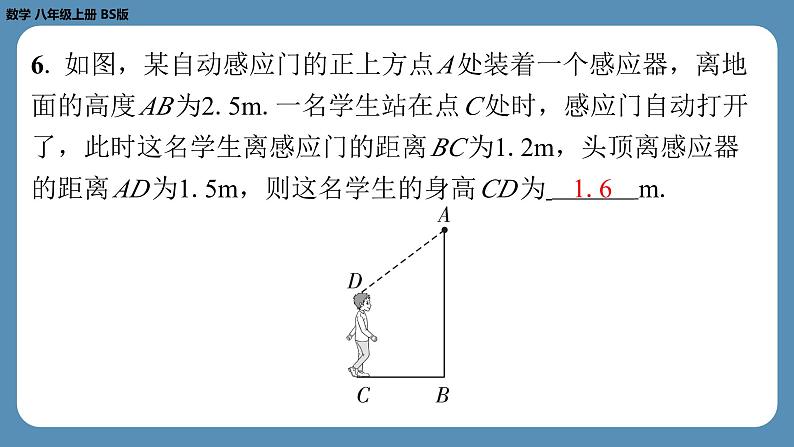
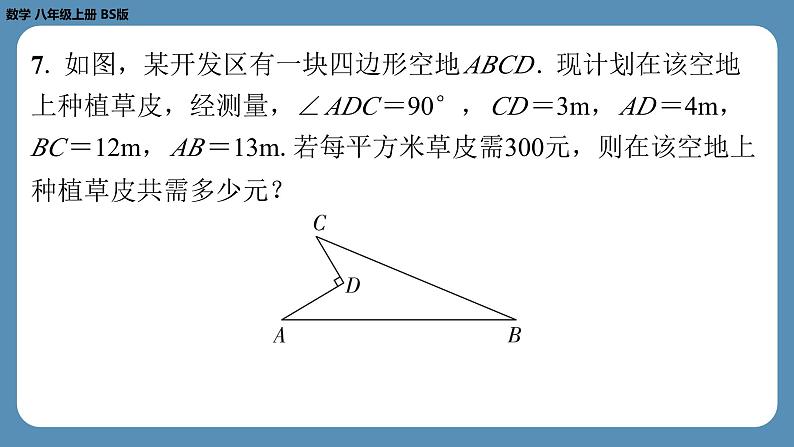
第二章 实 数专题1 勾股定理及其逆定理在几何图形中的应用 1. 在Rt△ ABC 中,已知∠ ACB =90°.若 AB =8, BC =6,则 AC 的长是( B )B2. 如图,将长为16cm的橡皮筋放置在数轴上,固定两端 A 和 B ,然后把中点 C 向上拉升6cm至点 D ,则橡皮筋被拉长了 ( A )A3. 如图,正方形 ABCD 的顶点 A , D 在数轴上,且点 A 表示的 数为-1,点 D 表示的数为0.若用圆规在数轴上截取 AE = AC , 则点 E 所表示的数为( C )C4. 如图,在Rt△ ABC 中,∠ B =90°,作 AC 的垂直平分线 l 交 BC 于点 D ,连接 AD . 若 AB =3, BC =9,则 BD 的长为 .4 5. 如图,有一张直角三角形纸片,两直角边 AC =6cm, BC = 8cm.现将△ ABC 折叠,使点 B 与点 A 重合,折痕为 DE ,则 BE 的长为 cm.5 6. 如图,某自动感应门的正上方点 A 处装着一个感应器,离地 面的高度 AB 为2.5m.一名学生站在点 C 处时,感应门自动打开 了,此时这名学生离感应门的距离 BC 为1.2m,头顶离感应器 的距离 AD 为1.5m,则这名学生的身高 CD 为 m.1.6 7. 如图,某开发区有一块四边形空地 ABCD . 现计划在该空地 上种植草皮,经测量,∠ ADC =90°, CD =3m, AD =4m, BC =12m, AB =13m.若每平方米草皮需300元,则在该空地上 种植草皮共需多少元?解:如图,连接 AC . 在Rt△ ACD 中,根据勾股定理,得 在△ ABC 中, AB2=132, BC2=122.又因为52+122=132,所以 AC2+ BC2= AB2.所以△ ABC 是直角三角形,且∠ ACB =90°. =24(m2).因为每平方米草皮需300元,所以在该空地上种植草皮共需24×300=7 200(元).8. 如图,将长方形 ABCD 沿对角线 AC 翻折,点 B 落在点 F 处, FC 交 AD 于点 E . (1)试说明:△ AFE ≌△ CDE ;(2)若 AB =4, BC =8,求图中阴影部分的面积. 9. 如图,在2×4的正方形网格中,△ ABC 的顶点都在小正方形 的顶点上,则点 A 到 BC 的距离等于 . 10. 如图,在正方形网格中,点 A , B , P 是网格线的交点,则 ∠ PAB +∠ PBA = °.答图45 【解析】如答图,延长 AP 交网格线于点 D ,连接 BD ,交网格 线于点 C ,可知点 D 在网格线交点处. PD2= BD2=12+22=5, PB2=12+32=10,所以 PD2+ BD2= PB2.所以△ BDP 是直角三 角形,且∠ PDB =90°.又因为 PD = BD ,所以△ PBD 是等腰 直角三角形.所以∠ DPB =45°.因为 PC ∥ AB ,所以∠ PAB = ∠ DPC ,∠ PBA =∠ CPB . 所以∠ PAB +∠ PBA =∠ DPC +∠ CPB =∠ DPB =45°.故答案为45.答图11. 如图,在一个长9cm、宽5cm的长方形纸片 ABCD 的中间位 置,放置一根正三棱柱的木块.木块的侧棱平行于 AD 且大于纸 片的宽 AD ,底面是边长为1cm的等边三角形.一只蚂蚁从点 A 处 爬行到点 C 处,求它爬行的最短路程.解:如图,将整个图形向上的一面展开到同一个平面中,中间 两个长方形表示三棱柱两个侧面的展开图.则蚂蚁爬行的最短路线为线段 AC . 在Rt△ ABC 中, AB =4+1+1+4=10(cm), BC =5cm, 12. 如图,在边长为6的正方形 ABCD 中,点 E 是边 CD 的中点, 将△ ADE 沿 AE 折叠至△ AFE ,延长 EF 交 BC 于点 G ,连接 AG ,且 AG 平分∠ BAF ,求 BG 的长. 所以△ ABG ≌△ AFG (ASA).所以 BG = FG . 设 BG = FG = x ,则 GC =6- x .因为点 E 为 CD 的中点,所以 CE = EF = DE =3,所以 EG =3+ x .在Rt△ CEG 中, CE2+ CG2= EG2,所以32+(6- x )2=(3+ x )2,解得 x =2.所以 BG 的长为2. (2)如图,Rt△ ABC 有 a2+ b2= c2.①由Rt△ ABC 是“平方倍三角形”,设 c2+ b2=3 a2.②把①代入②,得 a2+ b2+ b2=3 a2,即 a2= b2.所以 a = b . 演示完毕 谢谢观看
第二章 实 数专题1 勾股定理及其逆定理在几何图形中的应用 1. 在Rt△ ABC 中,已知∠ ACB =90°.若 AB =8, BC =6,则 AC 的长是( B )B2. 如图,将长为16cm的橡皮筋放置在数轴上,固定两端 A 和 B ,然后把中点 C 向上拉升6cm至点 D ,则橡皮筋被拉长了 ( A )A3. 如图,正方形 ABCD 的顶点 A , D 在数轴上,且点 A 表示的 数为-1,点 D 表示的数为0.若用圆规在数轴上截取 AE = AC , 则点 E 所表示的数为( C )C4. 如图,在Rt△ ABC 中,∠ B =90°,作 AC 的垂直平分线 l 交 BC 于点 D ,连接 AD . 若 AB =3, BC =9,则 BD 的长为 .4 5. 如图,有一张直角三角形纸片,两直角边 AC =6cm, BC = 8cm.现将△ ABC 折叠,使点 B 与点 A 重合,折痕为 DE ,则 BE 的长为 cm.5 6. 如图,某自动感应门的正上方点 A 处装着一个感应器,离地 面的高度 AB 为2.5m.一名学生站在点 C 处时,感应门自动打开 了,此时这名学生离感应门的距离 BC 为1.2m,头顶离感应器 的距离 AD 为1.5m,则这名学生的身高 CD 为 m.1.6 7. 如图,某开发区有一块四边形空地 ABCD . 现计划在该空地 上种植草皮,经测量,∠ ADC =90°, CD =3m, AD =4m, BC =12m, AB =13m.若每平方米草皮需300元,则在该空地上 种植草皮共需多少元?解:如图,连接 AC . 在Rt△ ACD 中,根据勾股定理,得 在△ ABC 中, AB2=132, BC2=122.又因为52+122=132,所以 AC2+ BC2= AB2.所以△ ABC 是直角三角形,且∠ ACB =90°. =24(m2).因为每平方米草皮需300元,所以在该空地上种植草皮共需24×300=7 200(元).8. 如图,将长方形 ABCD 沿对角线 AC 翻折,点 B 落在点 F 处, FC 交 AD 于点 E . (1)试说明:△ AFE ≌△ CDE ;(2)若 AB =4, BC =8,求图中阴影部分的面积. 9. 如图,在2×4的正方形网格中,△ ABC 的顶点都在小正方形 的顶点上,则点 A 到 BC 的距离等于 . 10. 如图,在正方形网格中,点 A , B , P 是网格线的交点,则 ∠ PAB +∠ PBA = °.答图45 【解析】如答图,延长 AP 交网格线于点 D ,连接 BD ,交网格 线于点 C ,可知点 D 在网格线交点处. PD2= BD2=12+22=5, PB2=12+32=10,所以 PD2+ BD2= PB2.所以△ BDP 是直角三 角形,且∠ PDB =90°.又因为 PD = BD ,所以△ PBD 是等腰 直角三角形.所以∠ DPB =45°.因为 PC ∥ AB ,所以∠ PAB = ∠ DPC ,∠ PBA =∠ CPB . 所以∠ PAB +∠ PBA =∠ DPC +∠ CPB =∠ DPB =45°.故答案为45.答图11. 如图,在一个长9cm、宽5cm的长方形纸片 ABCD 的中间位 置,放置一根正三棱柱的木块.木块的侧棱平行于 AD 且大于纸 片的宽 AD ,底面是边长为1cm的等边三角形.一只蚂蚁从点 A 处 爬行到点 C 处,求它爬行的最短路程.解:如图,将整个图形向上的一面展开到同一个平面中,中间 两个长方形表示三棱柱两个侧面的展开图.则蚂蚁爬行的最短路线为线段 AC . 在Rt△ ABC 中, AB =4+1+1+4=10(cm), BC =5cm, 12. 如图,在边长为6的正方形 ABCD 中,点 E 是边 CD 的中点, 将△ ADE 沿 AE 折叠至△ AFE ,延长 EF 交 BC 于点 G ,连接 AG ,且 AG 平分∠ BAF ,求 BG 的长. 所以△ ABG ≌△ AFG (ASA).所以 BG = FG . 设 BG = FG = x ,则 GC =6- x .因为点 E 为 CD 的中点,所以 CE = EF = DE =3,所以 EG =3+ x .在Rt△ CEG 中, CE2+ CG2= EG2,所以32+(6- x )2=(3+ x )2,解得 x =2.所以 BG 的长为2. (2)如图,Rt△ ABC 有 a2+ b2= c2.①由Rt△ ABC 是“平方倍三角形”,设 c2+ b2=3 a2.②把①代入②,得 a2+ b2+ b2=3 a2,即 a2= b2.所以 a = b . 演示完毕 谢谢观看
相关资料
更多









