初中数学人教版（2024）七年级上册第五章 一元一次方程5.1 方程课文内容课件ppt

这是一份初中数学人教版（2024）七年级上册第五章 一元一次方程5.1 方程课文内容课件ppt，共25页。PPT课件主要包含了学习目标，系数1通常省略不写，b-6等内容，欢迎下载使用。

1. 能用文字和数学符号表达等式的性质.2. 掌握等式的性质，能运用等式的性质进行等式的变形、解简单的一元一次方程，体会化归思想.
（1）3x－5＝298； （2）0.28－0.13y＝0.27y＋1．
你能看出下列方程的解吗？
发现是比较困难的.因此，本节课我们还要讨论怎样解方程.
像2x=3，x+1=3这样的简单方程，我们可以直接看出方程的解.
知识点1 等式的性质
像m＋n＝n＋m，x＋2x＝3x，3×3＋1＝5×2，3x＋1＝5y 这样的式子，都是等式. 用a＝b表示一般的等式. 　
关于等式的两个基本事实：（1）等式两边可以交换. 如果a=b，那么b=a.（2）相等关系可以传递. 如果a=b，b=c，那么a=c.
思考 在小学，我们已经知道：等式两边同时加（或减）同一个正数，同时乘同一个正数，或同时除以同一个不为0的正数、结果仍相等. 引入负数后，这些性质还成立吗？你可以用一些具体的数试一试.
3×3＋1＝5×2；3×3＋1+6___5×2+6；3×3＋1-6 ___5×2 -6；3×3＋1+(-1) ___5×2 +(-1) ；3×3＋1-(-1) ___5×2 -(-1) ；3×3＋1+0___5×2 +0.
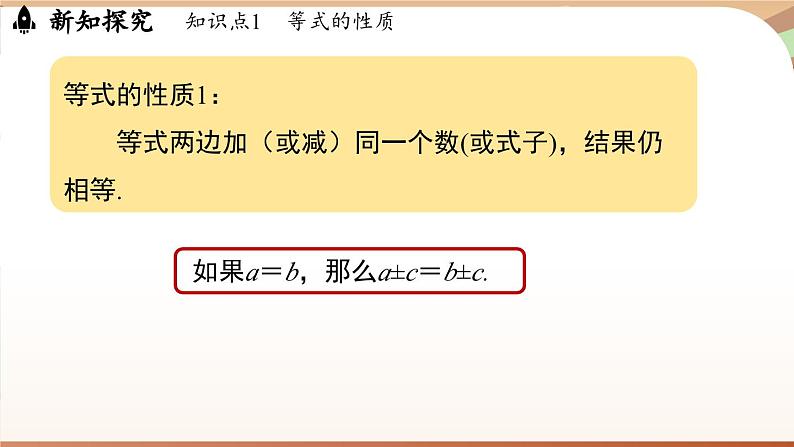
等式的性质1： 等式两边加（或减）同一个数(或式子)，结果仍相等.
如果a＝b，那么a±c＝b±c.
3×3＋1＝5×2；(3×3＋1)×6___5×2×6；(3×3＋1)÷6 ___5×2÷6；(3×3＋1)×(-2) ___5×2×(-2) ；(3×3＋1)÷(-2) ___5×2÷(-2) ；(3×3＋1) ×0___5×2×0.
等式的性质2: 等式两边乘同一个数，或除以同一个不为0的数，结果仍相等.
如果a=b，那么ac=bc；如果a=b (c≠0)，那么
例1 根据等式的性质填空，并说明依据：(1)如果2x=5-x，那么2x+_____ =5；(2)如果m+2n=5+2n，那么m= _____；
根据等式的性质1，等式两边加x，结果仍相等.
根据等式的性质1，等式两边减2n，结果仍相等.
根据等式的性质2，等式两边乘-7，结果仍相等.
根据等式的性质2，等式两边除以2，结果仍相等.
知识点2 利用等式的性质解方程
分析：要使方程x+7=26转化为x=a(常数)的形式，需要去掉方程左边的7，利用等式的性质1，方程两边减7就得出x的值.
解：(1)方程两边减7，得x+7-7=26-7.于是 x=19.
跟踪训练 利用等式的性质解下列方程，并检验：(1) x-5=6；(2)0.3x=45；
解：(1)方程两边加5，得x-5+5=6+5，于是x=11.检验：将x=11代入方程x-5=6的左边，得11-5=6.方程左右两边的值相等，所以x=11是方程的解.(2)方程两边除以0.3，得x=150.检验：将x=150代入方程0.3x=45的左边，得0.3×150=45.方程左右两边的值相等，所以x=150是方程的解.
利用等式的性质解简单的一元一次方程的一般步骤：第一步：利用等式的性质1，将方程左右两边同时加(或减)同一个数(或式子)，使方程逐步转化为一边只有含未知数的项，另一边只有常数项的形式；第二步：利用等式的性质2，将方程左右两边同时除以未知数的系数(或乘未知数系数的倒数)，即将未知数的系数化为1，从而求出方程的解.
判断等式的变形是否正确的方法当等式两边加、减或乘同一个数（或式子）时，变形均正确；当等式两边除以同一个数（或式子)时，要先判断这个数（或式子)是否为0，若确定该数(或式子)不为0，则该变形正确，否则错误.
2. 若等式 ac=bc 成立，则下列等式不一定成立的是( )A.ac +a =bc + = =b-bc.
两边同时加a, 得ac+a=bc+a.
两边同时乘b, 得abc= b2c.
当c≠0时，两边同时除以c,得a=b;当c=0时，不能得到a=b.
两边同时乘-1，得-ac=-bc,两边同时加b,得b-ac=b-bc.
3.利用等式的性质解方程：2x-1=3.
解：两边加1，得 2x-1+1=3+1.化简，得 2x=4. 两边除以2 ，得 x=2.
4. 利用等式的性质解方程并检验.