



- 考点13二次函数的应用(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版 试卷 0 次下载
- 考点13二次函数的应用(精讲)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版 试卷 0 次下载
- 考点14几何图形初步与平行线(精讲)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版 试卷 0 次下载
- 考点15三角形及全等(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版 试卷 0 次下载
- 考点15三角形及全等(精讲)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版 试卷 0 次下载
考点14几何图形初步与平行线(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版
展开1.(2023·广东·统考模拟预测)缓降机是火灾发生时避难的逃生设备,如图是厂商提供的缓降机安装示意图,图中呈现在三楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长(不计安全带).若某栋建筑的每个楼层高度皆为3公尺,则根据如图的安装方式在该建筑八楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长(不计安全带)为多少公尺?( )
A.21.7B.22.6C.24.7D.25.6
2.(2023·河北唐山·模拟预测)给出下列说法:(1)两条直线被第三条直线所截,同位角相等;
(2)不相等的两个角不是同位角;(3)直线外一点到这条直线的垂线段,叫做点到直线的距离;
(4)过一点作已知直线的平行线,有且只有一条;(5)垂直于同一条直线的两条直线互相垂直.
其中真命题有( )
A.个B.个C.个D.个
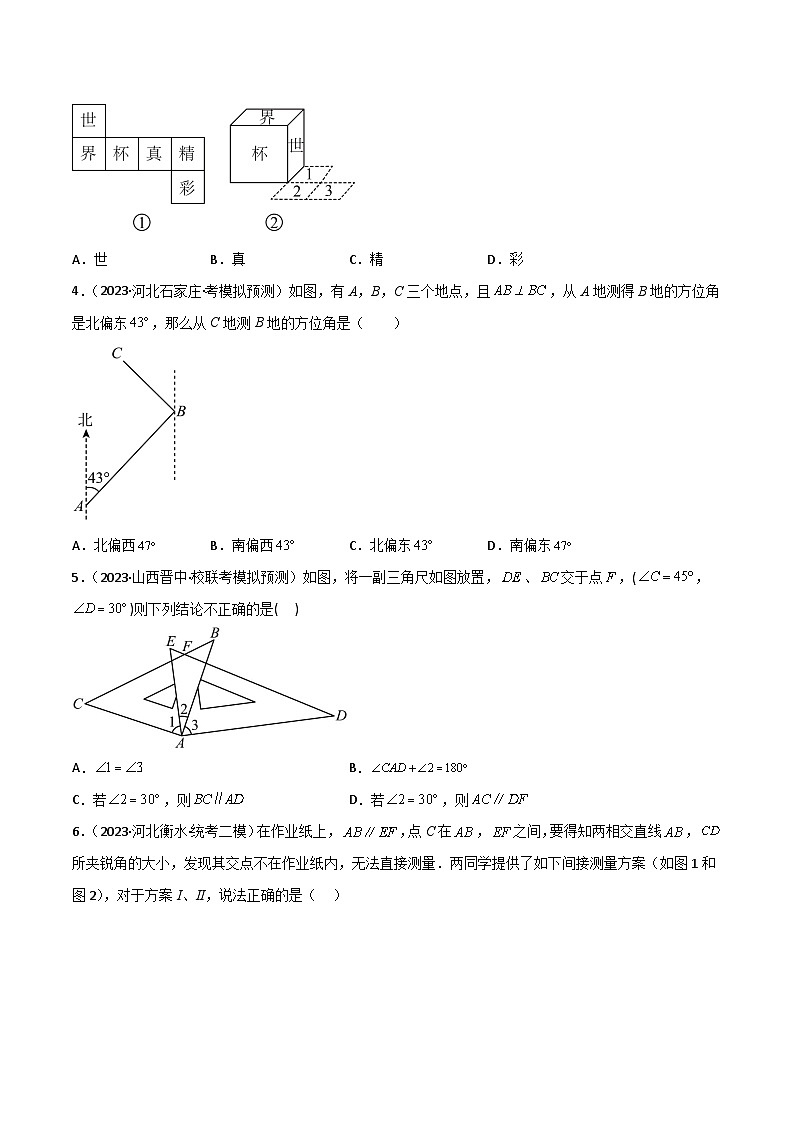
3.(2023·江西吉安·校考模拟预测)如图①所示的是一个正方体的表面展开图,将对应的正方体从如图②所示的位置依次翻过第1格、第2格,到第3格时正方体朝上的一面上的字是( )
A.世B.真C.精D.彩
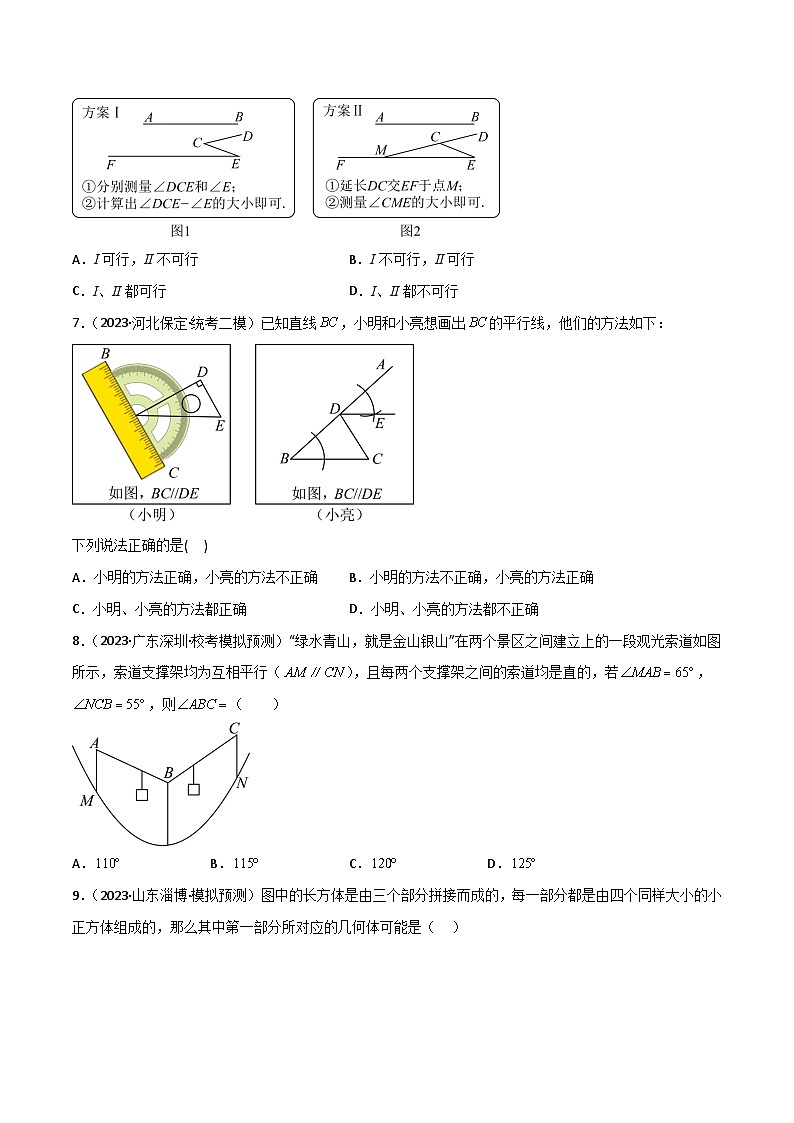
4.(2023·河北石家庄·考模拟预测)如图,有A,B,C三个地点,且,从A地测得B地的方位角是北偏东,那么从C地测B地的方位角是( )
A.北偏西B.南偏西C.北偏东D.南偏东
5.(2023·山西晋中·校联考模拟预测)如图,将一副三角尺如图放置,、交于点,(,)则下列结论不正确的是( )
A.B.
C.若,则D.若,则
6.(2023·河北衡水·统考二模)在作业纸上,,点C在,之间,要得知两相交直线,所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2),对于方案I、II,说法正确的是( )
A.I可行,II不可行B.I不可行,II可行
C.I、II都可行D.I、II都不可行
7.(2023·河北保定·统考二模)已知直线,小明和小亮想画出的平行线,他们的方法如下:
下列说法正确的是( )
A.小明的方法正确,小亮的方法不正确B.小明的方法不正确,小亮的方法正确
C.小明、小亮的方法都正确D.小明、小亮的方法都不正确
8.(2023·广东深圳·校考模拟预测)“绿水青山,就是金山银山”在两个景区之间建立上的一段观光索道如图所示,索道支撑架均为互相平行(),且每两个支撑架之间的索道均是直的,若,,则( )
A.B.C.D.
9.(2023·山东淄博·模拟预测)图中的长方体是由三个部分拼接而成的,每一部分都是由四个同样大小的小正方体组成的,那么其中第一部分所对应的几何体可能是( )
A.B.C.D.
10.(2023·浙江·模拟预测)在图中,实线所围成的多边形区域(阴影部分)是由四个全等正方形拼接而成的.现在若补上图中标有号码的其中一个全等小正方形,则可得到九个多边形区域(每个区域恰好含有五个全等小正方形),试问这九个多边形区域中,可以折成无盖的正方体容器的个数是( )
A.3B.4C.5D.6
11.(2023·河北沧州·校考二模)如图,不完整的数轴上有A,B两点,原点在A、B之间,沿原点将负半轴折叠到正半轴上,点A落在点B左侧4个单位长度处,则线段的中点表示的数为( )
A.2B.C.4D.
12.(2023·江苏无锡·统考二模)已知一个三角形的三边长分别为3、4、5,将这个三角形绕着最短的边所在直线旋转一周,得到一个几何体,那么这个几何体的侧面积为( )
A.B.C.D.
13.(2023·黑龙江大庆·校考模拟预测)如图是某几何体的展开图,则该几何体的体积为( )
A.B.C.D.
14.(2023·河南周口·校考模拟预测)如图,直线相交于点,若,则( )
A.B.C.D.
15.(2023·山东青岛·统考二模)如图的正方体纸盒,只有三个面上印有图案,下面四个平面图形中,经过折叠能围成此正方体纸盒的是( )
A. B. C. D.
16.(2023·吉林松原·校联考二模)如图,一片树叶标本部分磨损,用剪刀剪下(虚线)磨损的部位,此时,原来树叶标本的周长变小,能解释这一现象的数学道理是 .
17.(2023·浙江杭州·统考一模)如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,求此长方体的体积为 .
18.(2023·山东烟台·统考二模)七巧板是古代中国劳动人民的发明,是一种古老的中国传统智力游戏,其历史至少可以追溯到公元前一世纪.小明将一个边长为4的正方形制作成一副如图1所示的七巧板,取出其中的六块,拼成了一个(如图2),则的对角线AC的长度为 .
19.(2023·浙江·一模)日晷是我国古代利用日影测定时刻的一种计时仪器,它由“晷面”和“晷针”组成,古人常用的日晷有水平式日晷(图1)和赤道式日晷(图2).其中水平式日晷的“晷针”与“晷面”的夹角就是其所在位置的地理纬度且“晷面”与地面平行;赤道式日晷的“晷面”与赤道面平行当太阳光照在日晷上时,晷针的影子就会投向晷面.随着时间的推移,晷针的影子在晷面上慢慢地移动,以此来显示时刻.此外,水平式日晷的“晷面”刻度不均匀,赤道式日晷的“晷面”刻度则是均匀的.
(1)如图1,当水平式日晷放在纬度为 (即)位置时,晷针与晷面的夹角为 °.
(2)如图3,将两种日晷的“晷针”重合,n小时后,两种日晷对应的时刻一致,即两种晷“晷针”的影子所在的直线相交于点.此时与满足的关系式 .
20.(2023·广东深圳·校考模拟预测)在一副三角尺中,,,将它们按如图所示摆放在量角器上,边与量角器的刻度线重合,边与量角器的刻度线重合.将三角尺绕点以每秒的速度逆时针旋转,同时三角尺绕点以每秒的速度顺时针旋转,当三角尺的边与刻度线重合时两块三角尺都停止运动,则当运动时间 秒时,两块三角尺有一组边平行.
21.(2023·浙江温州·校考二模)如图,在中,平分,交边于点E,在边上取点F,连结,使.(1)求证:;(2)当时,求的度数.
22.(2023·浙江杭州·模拟预测)如图所示,M是线段AB上一定点,,C,D两点分别从点M,B出发以,的速度沿直线BA向左运动,运动方向如箭头所示(点C在线段AM上,点D在线段BM上).(1)当点C,D运动了时,求的值.
(2)若点C,D运时,总有,则_______.
(3)在(2)的条件下,N是直线AB上一点,且,求的值.
限时检测2:最新各地中考真题(40分钟)
1.(2023·山东青岛·统考中考真题)一个不透明小立方块的六个面上分别标有数字1,2,3,4,5,6,其展开图如图①所示.在一张不透明的桌子上,按图②方式将三个这样的小立方块搭成一个几何体,则该几何体能看得到的面上数字之和最小是( )
A.31B.32C.33D.34
2.(2022·贵州贵阳·统考中考真题)如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A.B.C.D.
3.(2023·山东临沂·统考中考真题)下图中用量角器测得的度数是( )
A.B.C.D.
4.(2023·湖南益阳·统考中考真题)下列正方体的展开图中,是轴对称图形的是( )
A. B. C. D.
5.(2023·青海·统考中考真题)如图,直线,相交于点O,,则的度数是( )
A.B.C.D.
6.(2023·山东·统考中考真题)如图是一正方体的表面展开图.将其折叠成正方体后,与顶点K距离最远的顶点是( )
A.A点B.B点C.C点D.D点
7.(2023·湖北宜昌·统考中考真题)如图,小颖按如下方式操作直尺和含角的三角尺,依次画出了直线a,b,c.如果,则的度数为( ).
A.B.C.D.
8.(2023·辽宁盘锦·统考中考真题)如图,直线,将一个含角的直角三角尺按图中方式放置,点E在上,边、分别交于点H、K,若,则等于( ).
A.B.C.D.
9.(2023·甘肃兰州·统考中考真题)如图,直线与相交于点O,则( )
A.B.C.D.
10.(2023·浙江金华·统考中考真题)如图,已知,则的度数是( )
A.B.C.D.
11.(2023·山东潍坊·统考中考真题)下列命题正确的是( )(多选题)
A.在一个三角形中至少有两个锐角 B.在圆中,垂直于弦的直径平分弦
C.如果两个角互余,那么它们的补角也互余 D.两条直线被第三条直线所截,同位角一定相等
12.(2023·江苏·统考中考真题)将直角三角板和直尺按照如图位置摆放,若,则的度数是( ).
A.B.C.D.
13.(2022·广西桂林·统考中考真题)如图,点C是线段AB的中点,若AC=2cm,则AB= cm.
14.(2023·山东烟台·统考中考真题)一杆古秤在称物时的状态如图所示,已知,则的度数为 .
15.(2023·江苏镇江·统考中考真题)如图,一条公路经两次转弯后,方向未变.第一次的拐角是,第二次的拐角是 °.
16.(2020·湖北恩施·中考真题)如图,直线,点在直线上,点在直线上,,,,则 .
17.(2022·江西·统考中考真题)沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为 .
18.(2023·辽宁沈阳·统考中考真题)如图,直线,直线分别与,交于点,,小明同学利用尺规按以下步骤作图:
(1)点为圆心,以任意长为半径作弧交射线于点,交射线于点;
(2)分别以点,为圆心,以大于的长为半径作弧,两弧在内交于点;
(3)作射线交直线于点;若,则 度.
19.(2021·浙江温州·统考中考真题)如图,是的角平分线,在上取点,使.
(1)求证:.(2)若,,求的度数.
20.(2020·江苏镇江·中考真题)如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.(1)求证:∠D=∠2;(2)若EF∥AC,∠D=78°,求∠BAC的度数.
21.(2020·湖北黄石·中考真题)如图,.
(1)求的度数;(2)若,求证:.
考点06分式方程(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版: 这是一份考点06分式方程(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版,文件包含考点06分式方程精练原卷版docx、考点06分式方程精练解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
考点04二次根式(精练)2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版: 这是一份考点04二次根式(精练)2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版,文件包含考点04二次根式精练原卷版docx、考点04二次根式精练解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
考点03分式(精讲)2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版: 这是一份考点03分式(精讲)2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版,文件包含考点03分式精讲原卷版docx、考点03分式精讲解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。












