

福建省泉州市永春县2023-2024学年八年级上学期期末质量监测数学试卷(含答案)
展开
这是一份福建省泉州市永春县2023-2024学年八年级上学期期末质量监测数学试卷(含答案),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
(满分:150分;考试时间:120分钟)
友情提示:所有答案必须填写到答题卡相应的位置上
学校:______姓名:______班级:______座位号:______
一、选择题:(本题共10个小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是最符合要求的)
1.4的平方根是( )
A.2;B.-2;C.;D.
2.下列计算正确的是( )
A.;B.;C.;D.
3.已知,则的估值范围正确的是( )
A.;B.;C.;D.
4.某同学在做“投掷一枚正方体股子”的实验时,连续抛了10次,共有3次掷得数字“1”,则掷得数字“1”的频率是( )
A.;B.;C.;D.
5.计算的结果是( )
A.;B.C.;D.
6.已知中,,求证:.若用反证法证这个结论,应先假设( )
A.;B.;C.;D.
7.等腰三角形有两边长为3和7,则该等腰三角形的周长为( )
A.13;B.17;C.13或17;D.10或13
8.我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释.现有三种类型卡片A、B、C,想要拼成如图所示长方形,则还需要C类型卡片( )张
A.3;B.4;C.5;D.6
第8题图
9.已知,,为正整数,且满足,则的取值不可能是( )
A.5;B.6;C.7;D.8
10.已知表示取三个数中最小的那个数.例如:,当时,则的取值范围为( )
A.;B.;C.;D.
二、填空题:(本题共6小题,每小题4分,共24分)
11.计算:______.
12.命题“对顶角相等”的逆命题是______.
13.已知,,则______.
14.如图,在等腰三角形中,,,是的中点,交于点,已知,则的值为______.
第14题图
15.如图,在中,,平分,若,,则的面积为______.
第15题图
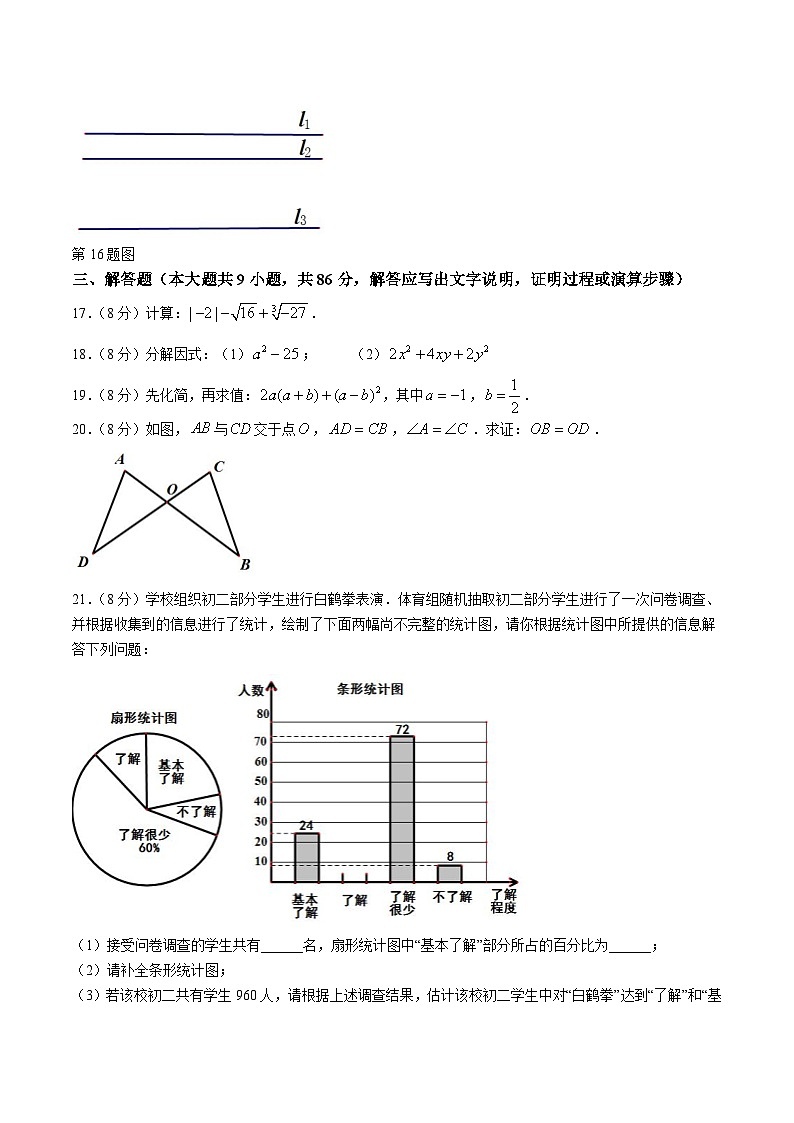
16.如图,相互平行的三条直线,,,与,与之间的距离分别为1,3,若在三条直线上各取一点,构造一个等腰直角三角形,那么作出的等腰直角三角形面积最大值为______.
第16题图
三、解答题(本大题共9小题,共86分,解答应写出文字说明,证明过程或演算步骤)
17.(8分)计算:.
18.(8分)分解因式:(1);(2)
19.(8分)先化简,再求值:,其中,.
20.(8分)如图,与交于点,,.求证:.
21.(8分)学校组织初二部分学生进行白鹤拳表演.体育组随机抽取初二部分学生进行了一次问卷调查、并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______名,扇形统计图中“基本了解”部分所占的百分比为______;
(2)请补全条形统计图;
(3)若该校初二共有学生960人,请根据上述调查结果,估计该校初二学生中对“白鹤拳”达到“了解”和“基本了解”程度的总人数.
22.(10分)如图,在边长为正方形纸板,四个角都剪去边长为的小正方形纸片,再把剩下的纸片延虚线折叠成一个无盖的长方体纸盒.
(1)长方体纸盒的底面边长为______(用含,的式子表示)
(2)若剪下的四个小正方形纸片拼成一个大正方形,恰好可作为纸盒的盖,当长方体的体积为时,求的值.
23.(10分)已知,在中,,为斜边的中点,.点在射线上,它到、两点的距离相等.
(1)如图,作出符合条件的点.(尺规作图,保留作图痕迹,不用写作法)
(2)若直角两条直角边的长分别为6和8,直线、相交于点,求的长.
24.(13分)我们把多项式及叫做完全平方式.如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法.
例如:求代数式的最小值.
由
可知,当时,有最小值,最小值是-8.
根据阅读材料,解决下列问题:
(1)求多项式的最小值;
(2)若,,判断、的大小关系,并说明理由;
(3)如图,为等边外的一点,,,,且,满足,求的长.
25.(13分)如图1,在中,.以边、边向外分别做正方形、正方形.
(1)连接,,求证:;
(2)连接,若,,求的值;
(3)若点是中点,连接并延长交为点,求证:.2023年秋季八年级期末质量监测数学试题参考答案
一、选择题(共40分)
1.D;2.A;3.B;4.D;5.A:6.C;7.B;8.C;9.D;10.B;
二、填空题(共24分)
11.;12.相等的角是对顶角;(或如果两个角相等,那么它们是对顶角)
13.39;14.4;
15.;16..
三、解答题(共86分)
17.(8分)
解:原式
18.(8分)
解:(1)原式
(2)原式
19.(8分)
解:原式
当,时
原式或
20.(8分)
证明:在和中
21.(8分)
解:(1)120名;20%;
(2)
正确补全条形统计图;
(3)(人)
答:该校初二学生中对“自鹤拳”达到“了解”和“基本了解”程度的总人数为320人.
22.(10分)
解:(1)
(2)由题意可得,即,
依题意得:
解得
即的值为8
23.(10分)
(1)可作线段的垂直平分线交于点
(或作或作)
如图所示点为所求
图一
(2)点到、两点的距离相等点在的垂直平分线上
点为中点
为的垂直平分线
设为,
①当,时,如图二
为的垂直平分线
在中,由勾股定理得:
解得
图二
②当,时,如图三
为的垂直平分线
在中,由勾股定理得:
解得
综上,的长为或.
24.(13分)
解:(1)
当时,有最小值,最小值是-15.
(2)
,
(3)
解得
如图,以为边向外作等边三角形,连接,则,
在中,由勾股定理得
为等边三角形
,
即
在和中
25.(13分)
解:(1)四边形,为正方形
,,
即
在和中
(2)在中,,
分别过点、作直线的垂线、,垂足分别为、
,,
在正方形中,
,
(3)如图,延长至点,使得
是中点
又
,
设,
在和中,
即
(以上答案仅供参考,其他正确方法酌情给分.)
相关试卷
这是一份福建省泉州市永春县2023-2024学年七年级上学期期末质量监测数学试卷,共10页。
这是一份福建省泉州市永春县2023-2024学年八年级上学期期末质量监测数学试卷(含答案),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年福建省泉州市永春县数学八上期末监测模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,如图,在中,按以下步骤作图,下列变形正确的是,下列说法正确的是等内容,欢迎下载使用。








