人教版九年级上册第二十三章 旋转23.2 中心对称23.2.1 中心对称图文ppt课件

这是一份人教版九年级上册第二十三章 旋转23.2 中心对称23.2.1 中心对称图文ppt课件，共30页。PPT课件主要包含了学习目标，从A旋转到C呢，从A旋转到D呢，讲授新课，旋转角为180°，观察与思考，中心对称的性质，轴对称，中心对称，折叠后两个图形重合等内容，欢迎下载使用。

1. 理解中心对称的定义；2. 探究中心对称的性质；(难点）3. 掌握中心对称的性质及其应用.（重点）
23.2.1 中心对称
从A旋转到B，旋转中心是什么？旋转角是多少？
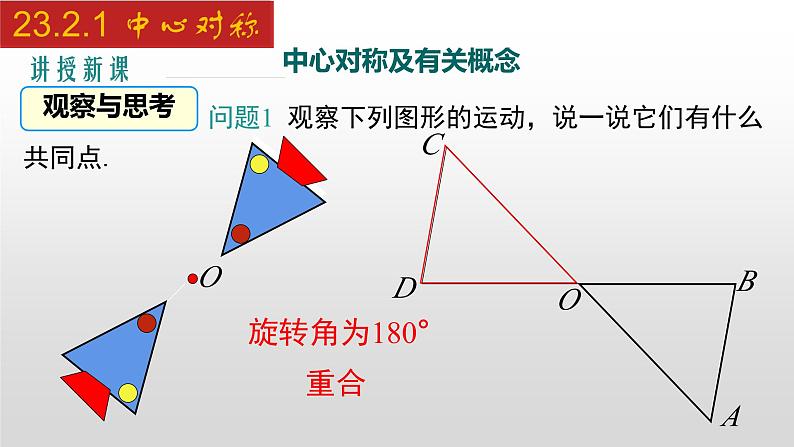
问题1 观察下列图形的运动，说一说它们有什么共同点.
把一个图形绕着某一点旋转 180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心(简称中心). 这两个图形在旋转后能够重合的对应点叫做关于对称中心的对称点.
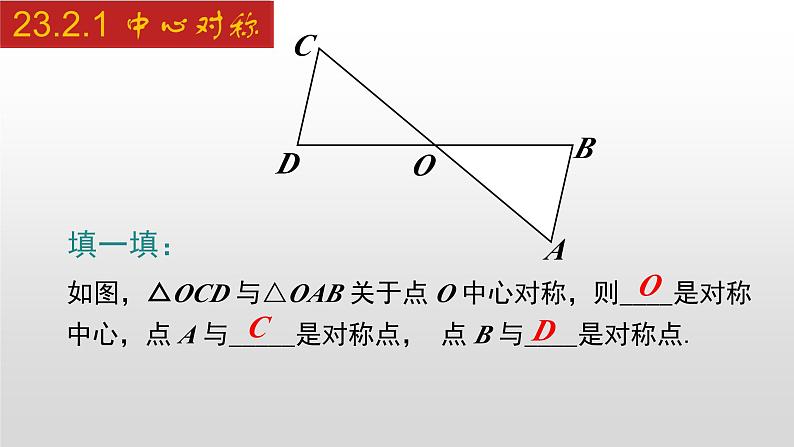
填一填： 如图，△OCD 与△OAB 关于点 O 中心对称，则____是对称中心，点 A 与_____是对称点， 点 B 与____是对称点.
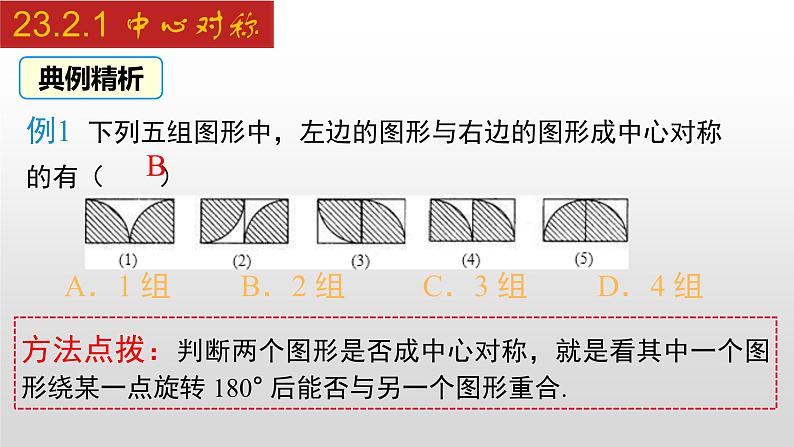
例1 下列五组图形中，左边的图形与右边的图形成中心对称的有（　　） A．1 组 B．2 组 C．3 组 D．4 组
方法点拨：判断两个图形是否成中心对称，就是看其中一个图形绕某一点旋转 180° 后能否与另一个图形重合.
1. 中心对称是一种特殊的旋转，其旋转角是180°；
2. 中心对称是两个图形之间一种特殊的位置关系；
3. 成中心对称的两个图形只有一个对称中心，对称中心可能在图形的外部、内部或图形上，对称点一定在对称中心两侧或与对称中心重合.
问题2 如图，旋转三角尺，画出△ABC 关于点 O 中心对称的△A′B′C′.
(1)OA = OA′、OB = OB′、 OC = OC′
下图中 △A′B′C′ 与 △ABC 关于点 O 是成中心对称,你能从图中找到哪些等量关系?
(2)△ABC≌△A′B′C′
1. 中心对称的两个图形，对称点所连线段都经过对称中心，并且被对称中心所平分（即每组对称点与对称中心三点共线）；
2. 中心对称的两个图形是全等形.
例2 如图，△ABC 与△A′B′C′ 关于点 O 成中心对称，则下列结论不成立的是（　　）A．点 A 与点 A′ 是对称点B．BO = B′OC．AB = A′B′D．∠ACB =∠C′A′B′
变式 如图，已知 △AOB 与 △DOC 成中心对称，△AOB 的面积是 12，AB＝6，则 △DOC 中 CD 边上的高为_____.
解析：设 AB 边上的高为 h，∵ △AOB 的面积是 12，AB＝6，∴ h＝4.又∵△AOB 与△DOC 成中心对称， ∴△COD≌△AOB.∴△DOC 中 CD 边上的高是 4.
例3 如图，已知 △ABC 与 △A′B′C′ 成中心对称，找出它们的对称中心 O.
解法1：根据观察，B、B′ 应是对称点，连接 BB′，用刻度尺找出 BB′ 的中点 O，则点 O 即为所求（如图）.
解法2：根据观察，B、B′ 及 C、C′ 应是两组对称点，连接 BB′、CC′ 相交于点 O，则点 O 即为所求（如图）.
注意：如果限定只用无刻度直尺作图，我们用解法2.
归纳总结：确定成中心对称的两个图形的对称中心的方法：①连接任意一组对称点，取这条线段的中点，这个中点就是对称中心；②连接任意两组对称点，两条线段的交点就是对称中心.
例4 (1)如图1，选择点 O 为对称中心，画出点 A 关于点 O 的对称点 A'；(2)如图2，选择点 O 为对称中心，画出与△ABC 关于点 O 对称的△A'B'C'.
(1) 如图 1，连接 AO 并延长到 A'，使 OA' = OA，即可得到点 A 的对称点 A'；
(2) 如图 2，作出 A，B，C 三点关于点 O 的对称点 A'，B'，C'，顺次连接 A'B'，B'C'，C'A'，则△A'B'C' 即为所作.
练一练 如图，已知四边形 ABCD 和点 O，试画出四边形 ABCD 关于点 O 成中心对称的图形 A'B'C'D'.
分析：要画出四边形 ABCD 关于点 O 成中心对称的图形，只要画出 A，B，C，D 四点关于点 O 的对称点，再顺次连接各对称点即可.
① 连接 AO 并延长到 A'，使 OA' = OA，得到点 A 的对称点 A'；
② 同理，可作出点 B，C，D 的对称点 B'，C'，D'；
③ 顺次连接 A'，B'，C'，D'，则四边形 A'B'C'D' 即为所作.
中心对称与轴对称的异同
1. 判断正误： （1）轴对称的两个图形一定是全等形，但全等的两个图形不一定是轴对称的图形.（ ） （2）成中心对称的两个图形一定是全等形，但全等的两个图形不一定是成中心对称的图形. （ ） （3）全等的两个图形，不是成中心对称的图形，就是成轴对称的图形. （ ）
2. 如下所示的 4 组图形中，左边数字与右边数字成中心对称的有 （ ） A. 1 组 B. 2 组 C. 3 组 D. 4 组
3. 如图，已知 △AOB 与 △DOC 成中心对称，△AOB 的周长是 8，AB＝3，则 OC + OD＝（　　） A. 3　　　 B. 5　　　　　　 C. 6　　 D. 8
4．将四个“米”字格的正方形内涂上阴影，其 中既是轴对称图形，又是中心对称图形的是(　　)
5. 如图，已知等边△ABC 和点 O，画△A′B′C′，使△A′B′C′ 和 △ABC 关于点 O 成中心对称.
6. 如图，△ABO 与△CDO 关于 O 点中心对称，点 E，F在线段 AC 上，且 AF = CE．求证：DF = BE．
证明：∵△ABO 与△CDO 关于 O 点中心对称，
∴BO = DO，AO = CO.
∴AO－AF = CO－CE.
在△FOD 和△EOB 中，
∴△FOD≌△EOB（SAS）.
对称点的连线经过对称中心，且被对称中心平分
应用1：作图形关于某点对称的图形；应用2：找出对称中心.