数学8.2离散型随机变量及其分布列完美版课件ppt

这是一份数学8.2离散型随机变量及其分布列完美版课件ppt，共30页。PPT课件主要包含了导入课题，新知探究，离散型随机变量的均值，数学期望，解X的分布列为，···，X的分布列为，答案A，故X的分布列为等内容，欢迎下载使用。

甲、乙两名射箭运动员射中目标箭靶的环数的分布列如下表所示.
思考：如何比较甲、乙两人射箭水平的高低？
首先比较击中的平均环数，如果平均环数相同，再比较稳定性.
即甲射中平均环数的稳定值为9，该平均值的大小可以反映甲运动员的射箭水平.
所以，从平均值的角度比较，甲运动员的射箭水平比乙运动员高.
一般地，若离散型随机变量X的分布列为：
求随机变量的均值关键是写出分布列，一般分为四步：(1)确定X的可能取值；(2)计算出P(X＝k)；(3)写出分布列；(4)利用E(X)的计算公式计算E(X)．
例1 在篮球比赛中，罚球命中1次得1分，不中得0分. 如果某运动员罚球命中的概率为0.8，那么他罚球1次的得分X的均值是多少?
解：因为P(X=1)=0.8，P(X=0)=0.2, 所以E(X)=0 x 0.2 + 1 x 0.8=0.8. 即该运动员罚球1次的得分X的均值是0.8.
一般地，如果随机变量X服从两点分布，那么 E(X)=0 x (1-p) + 1 x p = p
例2 抛掷一枚质地均匀的骰子，设出现的点数为X，求X的均值.
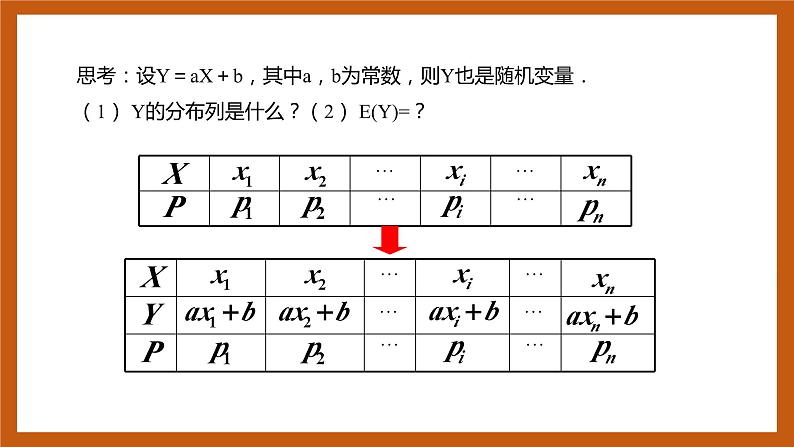
思考：设Y＝aX＋b，其中a，b为常数，则Y也是随机变量．（1） Y的分布列是什么？（2） E(Y)=？
E(aX+b)=aE(X)+b
离散型随机变量均值的运算性质
(1) E(X＋b)＝E(X)＋b，(2) E(aX)＝aE(X)，(3) E(aX＋b)＝aE(X)＋b.
例3 猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名.某嘉宾参加猜歌名节目，猜对每首歌曲的歌名相互独立，猜对三首歌曲A，B，C歌名的概率及猜对时获得相应的公益基金如表所示.
规则如下:按照A，B，C的顺序猜，只有猜对当前歌曲的歌名才有资格猜下一首.求嘉宾获得的公益基金总额X的分布列及均值.
分析:根据规则，公益基金总额X的可能取值有四种情况：猜错A，获得0元基金；猜对A而猜错B，获得1000元基金；猜对A 和B而猜错C，获得3000元基金；A，B， C全部猜对，获得6000元基金.因此X是一个离散型随机变量，利用独立条件下的乘法公式可求分布列.
则X的均值为： E(X)=0 x 0.2 + 1000 x 0.32 + 3000 x 0.288 + 6000 x 0.192 = 2336
【例1】 袋中有4个红球,3个白球,从袋中随机取出4个球.设取出一个红球得2分,取出一个白球得1分,试求得分X的均值.
解 X的所有可能取值为5,6,7,8.当X=5时,表示取出1个红球,3个白球,
规律方法　求离散型随机变量均值的步骤：(1)确定离散型随机变量X的取值.(2)写出分布列,并检查分布列的正确与否.(3)根据公式求出均值.
盒中装有5节同品牌的五号电池,其中混有两节废电池.现在无放回地每次取一节电池检验,直到取到好电池为止,求抽取次数X的分布列及均值.
故抽取次数X的分布列为
【例2】 已知随机变量X的分布列为
若Y=-2X,则E(Y)=　　　　　. 
本例条件不变,若ξ=aX+3,且E(ξ)=- ,求a的值.
规律方法　若给出的随机变量ξ与X的关系为ξ=aX+b,a,b为实数.一般思路是先求出E(X),再利用公式E(ξ)=E(aX+b)=aE(X)+b求出E(ξ).
已知随机变量ξ和η,其中η=12ξ+7,且E(η)=34,若ξ的分布列如下表,则m的值为(　　)
解析 因为η=12ξ+7,所以E(η)=12E(ξ)+7,
【例3】 (2022河南郑州月考)有9张相同的卡片,分别标有数字1,2,3,4,5,6,7,8,9,从中随机抽取3张.(1)求抽取的3张卡片上的数字中任意2个均不在下表的同一行,且不在同一列的概率;(2)若抽取的3张卡片上的3个数字均为奇数或均为偶数记为情况①;若3个数字位于下表的同一行或同一列或同一对角线上记为情况②.当同时满足①②两种情况得3分;仅满足情况①得2分;仅满足情况②得1分;其他情况得0分.求得分的分布列及均值.
规律方法　解答应用类问题时,首先把问题概率模型化,然后利用有关概率的知识去分析相应各事件可能性的大小,并列出分布列,最后利用公式求出相应概率.
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元,设1件产品的利润(单位:万元)为X.(1)求X的分布列;(2)求1件产品的平均利润(即X的均值);(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.若此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
(2)E(X)=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34(万元).
(3)设技术革新后的三等品率为x,则此时1件产品的平均利润为E(X)=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01=4.76-x(0≤x≤0.29),依题意,知E(X)≥4.73,即4.76-x≥4.73,解得x≤0.03,所以三等品率最多为3%.