高考数学一轮复习【考点题型归纳讲练】导学案（新高考专用）第03课时圆的方程及直线与圆的位置关系(原卷版+解析)

这是一份高考数学一轮复习【考点题型归纳讲练】导学案（新高考专用）第03课时圆的方程及直线与圆的位置关系(原卷版+解析)，共35页。

【回归教材】
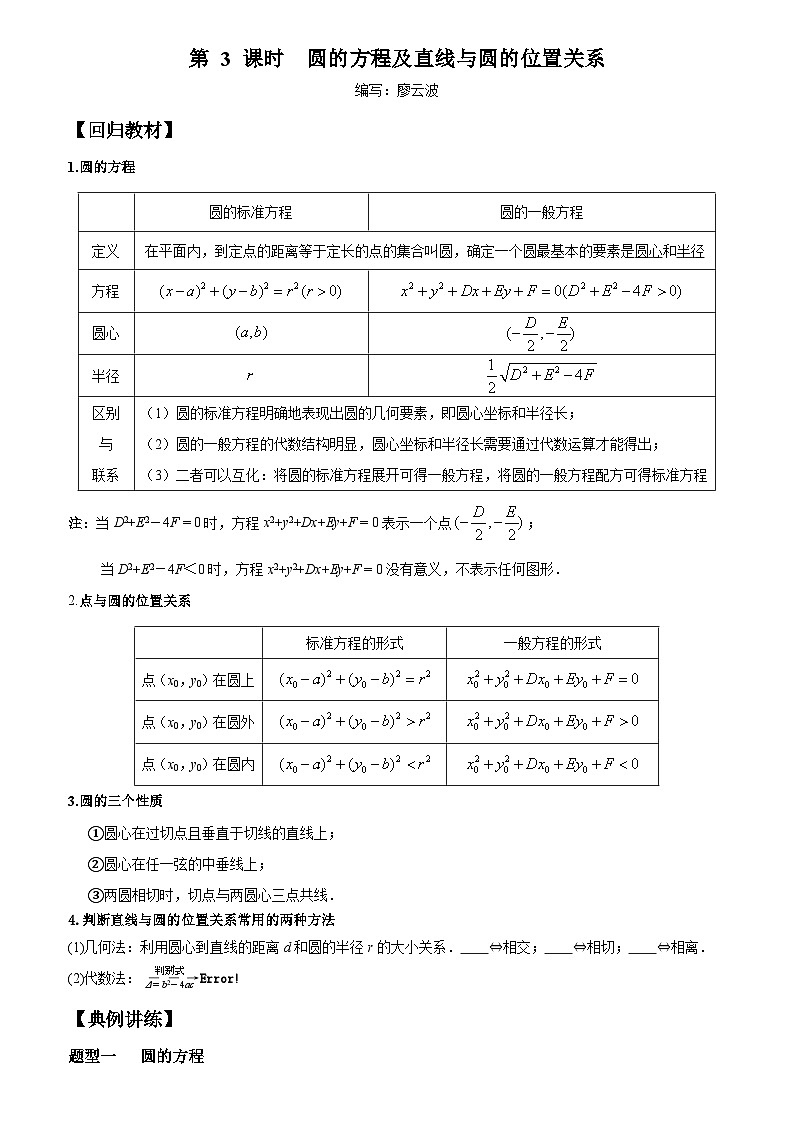
1.圆的方程
注：当D2+E2－4F = 0时，方程x2+y2+Dx+Ey+F = 0表示一个点；
当D2+E2－4F＜0时，方程x2+y2+Dx+Ey+F = 0没有意义，不表示任何图形．
2.点与圆的位置关系
3.圆的三个性质
①圆心在过切点且垂直于切线的直线上；
②圆心在任一弦的中垂线上；
③两圆相切时，切点与两圆心三点共线．
4.判断直线与圆的位置关系常用的两种方法
(1)几何法：利用圆心到直线的距离d和圆的半径r的大小关系． ⇔相交； ⇔相切； ⇔相离．
(2)代数法：eq \(――→,\s\up7(判别式),\s\d5(Δ＝b2－4ac))eq \b\lc\{\rc\ (\a\vs4\al\c1(>0⇔ ；,＝0⇔ ；,<0⇔ .))
【典例讲练】
题型一 圆的方程
【例1-1】求经过点P(5，1)，圆心为点C(8，－3)的圆的方程：
【例1-2】(1)已知的三个顶点分别为，，，求其外接圆方程；
(2)圆心在直线上，且与直线相切于点，求圆的方程.
【例1-3】若两定点，，动点M满足，则动点M的轨迹围成区域的面积为（ ）．
A．B．C．D．
【例1-4】已知是圆的一条直径的两个端点，证明圆的方程是．
归纳总结：
【练习1-1】若圆的圆心在直线上，则C的半径为______．
【练习1-2】圆心在直线2x－3y－1＝0上的圆与x轴交于A（1，0）、B（3，0）两点，则圆的方程为________．
【练习1-3】公元前3世纪，古希腊数学家阿波罗尼斯（）在《平面轨迹》一书中，曾研究了众多的平面轨迹问题，其中有如下结果：平面内到两定点距离之比等于已知数的动点轨迹为直线或圆.后世把这种圆称之为阿波罗尼斯圆.已知直角坐标系中，，，且满足，则点的运动轨迹方程为____________，点到直线的最小距离为__________.
题型二 直线与圆的位置关系
【例2-1】在平面直角坐标系xOy中，直线与圆C：x2+y2-2x-2y-2＝0的位置关系_____.
【例2-2】直线与圆相切，则（ ）
A．3B．C．或1D．3或
【例2-3】已知直线与圆相交，则实数k的取值范围是（ ）
A．B．
C．D．
归纳总结：
【练习2-1】若圆上恰有2个点到直线y=x+b的距离等于1，则b的取值范围是( )
A．B．
C．D．
【练习2-2】直线与圆的位置关系为（ ）
A．相切B．相交
C．相离D．由的取值确定
题型三 圆的切线
【例3-1】过圆上一点作圆的切线，则直线的方程为______．
【例3-2】过点作圆的两条切线，切点分别为A，B，求直线的方程．
【例3-3】由直线上的点向圆引切线（为切点），则线段的最小长度为________．
归纳总结：
【练习3-1】已知圆．求满足下列条件的切线方程．
(1)过点；
(2)过点．
【练习3-2】已知圆：，点是直线上的动点，过作圆的两条切线，切点分别为，，则的最小值为（ ）
A．B．C．D．
题型四 范围问题
【例4-1】设为圆上一点，则点到直线距离的取值范围是（ ）
A．B．C．D．
【例4-2】在平面直角坐标系中， 已知点 是圆心在原点， 半径为 的圆上的点， 且 ，若点 的坐标为 ， 则 的最大值为（ ）
A．B．C．D．
归纳总结：
【练习4-1】在平面直角坐标系xOy中，直线与圆C：x2+y2-2x-2y-2＝0交于A，B两点，则|AB|的最小值为________．
【练习4-2】已知平面向量满足，则的最小值是（ ）
A．B．C．D．
【请完成课时作业（五十二）
【课时作业（五十二）】
A组 基础题
1．圆心在坐标原点，半径为2的圆的标准方程是（ ）
A．B．
C．D．
2．已知z为复数，且，则的取值范围是（ ）
A．B．C．D．
3．已知双曲线的渐近线与圆相切，则a=（ ）
A．B．C．D．
4．已知直线 l 过点，则直线 l 被圆O：截得的弦长的最小值为（ ）
A．3B．6C．D．
5．己知点，直线与圆相切于点，则的值为（ ）
A．B．C．D．
6．直线与圆相交，所得弦长为整数，这样的直线有（ ）条
A．10 B．9 C．8 D．7
7．若，分别为圆：与圆：上的动点，为直线上的动点，则的最小值为（ ）
A．B．6C．9D．12
8．已知，为圆：上两点，且，点在直线：上，则的最小值为（ ）
A．B．
C．D．
9．【多选题】在平面直角坐标系中，已知圆：，则下列说法正确的是（ ）
A．若，则点在圆外
B．圆与轴相切
C．若圆截轴所得弦长为，则
D．点到圆上一点的最大距离和最小距离的乘积为
10．方程表示圆，则的取值范围为______．
11．已知直线与圆相交于两点，则=__________．
12．从圆外一点向圆引切线，则此切线的长为______．
13．已知平面上两定点A、B满足，动点P、Q分别满足，则的取值范围是___．
B组 能力提升
1．已知向量，，共面，且均为单位向量，，则的取值范围是（ ）
A．B．
C．D．
2．已知P是直线l：x＋y－7＝0上任意一点，过点P作两条直线与圆C：相切，切点分别为A，B.则｜AB｜的最小值为（ ）
A．B．C．D．
3．已知函数是偶函数，则f（x）的图象与y轴交点的纵坐标的最大值是（ ）.
A．6B．4C．2D．0
4．已知直线，若P为l上的动点，过点P作的切线，切点为A、B，当最小时，直线的方程为__________.
5．平面直角坐标系中，点、、，动点在的内切圆上，则的最小值为_________.
圆的标准方程
圆的一般方程
定义
在平面内，到定点的距离等于定长的点的集合叫圆，确定一个圆最基本的要素是圆心和半径
方程
圆心
半径
区别与
联系
（1）圆的标准方程明确地表现出圆的几何要素，即圆心坐标和半径长；
（2）圆的一般方程的代数结构明显，圆心坐标和半径长需要通过代数运算才能得出；
（3）二者可以互化：将圆的标准方程展开可得一般方程，将圆的一般方程配方可得标准方程
标准方程的形式
一般方程的形式
点（x0，y0）在圆上
点（x0，y0）在圆外
点（x0，y0）在圆内
第 3 课时 圆的方程及直线与圆的位置关系
编写：廖云波
【回归教材】
1.圆的方程
注：当D2+E2－4F = 0时，方程x2+y2+Dx+Ey+F = 0表示一个点；
当D2+E2－4F＜0时，方程x2+y2+Dx+Ey+F = 0没有意义，不表示任何图形．
2.点与圆的位置关系
3.圆的三个性质
①圆心在过切点且垂直于切线的直线上；
②圆心在任一弦的中垂线上；
③两圆相切时，切点与两圆心三点共线．
4.判断直线与圆的位置关系常用的两种方法
(1)几何法：利用圆心到直线的距离d和圆的半径r的大小关系．dr⇔相离．
(2)代数法：eq \(――→,\s\up7(判别式),\s\d5(Δ＝b2－4ac))eq \b\lc\{\rc\ (\a\vs4\al\c1(>0⇔相交；,＝0⇔相切；,<0⇔相离.))
【典例讲练】
题型一 圆的方程
【例1-1】求经过点P(5，1)，圆心为点C(8，－3)的圆的方程：
【答案】；
【解析】两点间的距离公式可知，圆的半径长为，
因此，圆的方程为.
【例1-2】(1)已知的三个顶点分别为，，，求其外接圆方程；
(2)圆心在直线上，且与直线相切于点，求圆的方程.
【答案】(1)；(2)
【解析】
【分析】
(1)直接利用圆的方程的一般式建立方程组，进一步确定圆的方程；
(2)利用圆的标准式和二元一次方程组的解法求出圆的方程．
【详解】
(1)的三个顶点分别为，，，
设外接圆的方程为，
故解得：
故圆的方程为．
(2)设圆的标准方程为，
则有解得，，，
所求圆的方程为
【例1-3】若两定点，，动点M满足，则动点M的轨迹围成区域的面积为（ ）．
A．B．C．D．
【答案】D
【解析】
【分析】
根据给定条件求出动点M的轨迹方程，再确定轨迹即可计算作答.
【详解】
设，依题意，，化简整理得：，
因此，动点M的轨迹是以为圆心，2为半径的圆，
所以动点M的轨迹围成区域的面积为.
故选：D
【例1-4】已知是圆的一条直径的两个端点，证明圆的方程是．
【答案】证明见解析
【解析】
【分析】
设圆上任意一点为，根据圆的几何性质得到，向量坐标化可得到结果.
【详解】
是圆的一条直径的两个端点，
设圆上任意一点为，根据圆的几何性质得到

代入上式并变形得到：.
故题目得证.
归纳总结：
【练习1-1】若圆的圆心在直线上，则C的半径为______．
【答案】
【解析】
【分析】
先求得参数D，再去求C的半径即可解决.
【详解】
圆的圆心为
则有，则，则C的半径为
故答案为：
【练习1-2】圆心在直线2x－3y－1＝0上的圆与x轴交于A（1，0）、B（3，0）两点，则圆的方程为________．
【答案】＝2
【解析】
【分析】
由圆与轴的交点和的坐标，根据垂径定理得到圆心在直线上，又圆心在直线上，联立两直线方程组成方程组，求出方程组的解集得到交点坐标即为圆心坐标，由求出的圆心坐标和的坐标，利用两点间的距离公式求出圆心到的距离即为圆的半径，由圆心和半径写出圆的方程即可．
【详解】
解：由题意得：圆心在直线上，
又圆心在直线上，令，得
圆心的坐标为，又，
半径，
则圆的方程为．
故答案为：
【练习1-3】公元前3世纪，古希腊数学家阿波罗尼斯（）在《平面轨迹》一书中，曾研究了众多的平面轨迹问题，其中有如下结果：平面内到两定点距离之比等于已知数的动点轨迹为直线或圆.后世把这种圆称之为阿波罗尼斯圆.已知直角坐标系中，，，且满足，则点的运动轨迹方程为____________，点到直线的最小距离为__________.
【答案】
【解析】（1），
化简为；
（2）点到直线的距离的最小值是圆心到直线的距离减半径，
即.
故答案为：；.
题型二 直线与圆的位置关系
【例2-1】在平面直角坐标系xOy中，直线与圆C：x2+y2-2x-2y-2＝0的位置关系_____.
【答案】相交
【解析】
由，得，即直线过定点，
圆C：x2+y2-2x-2y-2＝0的标准方程为，圆心，半径，
因为，所以在圆内，
故答案为：.相交
【例2-2】直线与圆相切，则（ ）
A．3B．C．或1D．3或
【答案】D
【解析】
【分析】
利用题给条件列出关于a的方程，解之即可求得a的值.
【详解】
圆的圆心坐标为，半径为
又直线与圆相切，
则，解之得或，
故选：D．
【例2-3】已知直线与圆相交，则实数k的取值范围是（ ）
A．B．
C．D．
【答案】D
【解析】
【分析】
根据直线与圆相交，则圆心到直线的距离小于半径求解即可
【详解】
由题意，圆心到直线的距离，即，解得
故选：D
归纳总结：
【练习2-1】若圆上恰有2个点到直线y=x+b的距离等于1，则b的取值范围是( )
A．B．
C．D．
【答案】B
【解析】依题意可得圆心到直线的距离.∵∴，解得或，故选B.
【练习2-2】直线与圆的位置关系为（ ）
A．相切B．相交
C．相离D．由的取值确定
【答案】A
【解析】
【分析】
利用圆心到直线的距离与半径的大小关系进行判断.
【详解】
因为圆心到直线的距离，即为圆的半径，所以可知直线与圆相切.
故选：A．
题型三 圆的切线
【例3-1】过圆上一点作圆的切线，则直线的方程为______．
【答案】x-2y-5=0
【解析】
【分析】
本题考查在某点切线问题，根据，可得直线的斜率，再利用点斜式求直线的方程．
【详解】
根据题意易知直线得斜率存在，则，即．
则直线得方程为：即：x-2y-5=0．
故答案为：x-2y-5=0．
【例3-2】过点作圆的两条切线，切点分别为A，B，求直线的方程．
【答案】
【解析】
【分析】
求出圆心为，得到以为直径的圆的方程为.判断出
直线为两圆的公共弦，两圆方程相减，消去二次项，即可求出直线的方程.
【详解】
圆化为标准方程为，设圆心为，半径R=5.
所以连线中点坐标,而.
故以为直径的圆的方程为.
因为是圆的两条切线，切点分别为A，B，
所以A，B为圆和的交点，
所以直线为两圆的公共弦，两圆方程相减，消去二次项，可得：
.
所以直线的方程：.
【例3-3】由直线上的点向圆引切线（为切点），则线段的最小长度为________．
【答案】
【解析】
【分析】
利用切线长定理，结合点到直线距离公式计算作答.
【详解】
圆的圆心，半径，点到直线的距离，
于是得，当且仅当垂直于直线时取“=“，
所以线段的最小长度为.
故答案为：
归纳总结：
【练习3-1】已知圆．求满足下列条件的切线方程．
(1)过点；
(2)过点．
【答案】(1)
(2)或
【解析】
【分析】
（1）由题知点在圆，且切线斜率存在，进而根据切线与直线垂直求得切线斜率，最后根据点斜式求解即可；
（2）根据题意，分斜率不存在和存在两种情况讨论求解即可.
(1)
解：因为圆的圆心为，半径为，点在圆上，
所以过点的切线斜率存在，且其与直线垂直，
因为，所以，所求切线的斜率为，
所以，所求切线方程为，即：.
(2)
解：因为圆的圆心为，半径为，
所以，当过点的切线斜率不存在时，其方程为，满足题意；
当切线斜率存在时，设斜率为，则其方程为，即，
所以，圆心到切线的距离为，解得，
所以，切线方程为，即：.
综上，所求切线方程为或
【练习3-2】已知圆：，点是直线上的动点，过作圆的两条切线，切点分别为，，则的最小值为（ ）
A．B．C．D．
【答案】B
【解析】
【分析】
利用面积相等求出.设，得到.利用几何法分析出，即可求出的最小值.
【详解】
圆：化为标准方程：，其圆心,半径.
过点P引圆C的两条切线,切点分别为点A、B,如图：
在△PAC中,有，即，变形可得：.
设，则.
所以当的值即x最小时，的值最大，此时最小.
而的最小值为点C到直线的距离，即，
所以.
故选：B
题型四 范围问题
【例4-1】设为圆上一点，则点到直线距离的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】圆，圆心，半径3，
圆心到直线距离，
所以点到直线距离的最短为0，最长为，
故选：B.
【例4-2】在平面直角坐标系中， 已知点 是圆心在原点， 半径为 的圆上的点， 且 ，若点 的坐标为 ， 则 的最大值为（ ）
A．B．C．D．
【答案】B
【解析】
【分析】
由题可判断AC的中点为原点，从而，然后用坐标表示出所求，利用点B在圆上化简可得.
【详解】
因为，所以AC为单位圆的直径，O为AC的中点.
设，则，
所以
所以
因为，所以
故选：B
归纳总结：
【练习4-1】在平面直角坐标系xOy中，直线与圆C：x2+y2-2x-2y-2＝0交于A，B两点，则|AB|的最小值为________．
【答案】
【解析】
由，得，即直线过定点，
圆C：x2+y2-2x-2y-2＝0的标准方程为，圆心，半径，
因为，所以在圆内，，
当时最短，是的中点，所以
故答案为：.
【练习4-2】已知平面向量满足，则的最小值是（ ）
A．B．C．D．
【答案】D
【解析】
【分析】
先设，由设在直线上，由得，进而得出在以为圆心，1为半径的圆上，将的最小值转化为圆上点到直线上点距离的最小值即可求解.
【详解】
建立平面直角坐标系，设，由，不妨设，
又，不妨设在直线上，又可得，即，
则，设，则，则，即，则在以为圆心，1为半径的圆上；
又，则的最小值等价于的最小值，即以为圆心，1为半径的圆上一点
到直线上一点距离的最小值，即圆心到直线的距离减去半径，即，则的最小值是.
故选：D.
【点睛】
本题关键点在于建立坐标系后设，由得出在直线上，再由得在以为圆心，1为半径的圆上，进而转化为圆上点到直线上点距离的最小值求解即可.
【请完成课时作业（五十二）】
【课时作业（五十二）】
A组 基础题
1．圆心在坐标原点，半径为2的圆的标准方程是（ ）
A．B．
C．D．
【答案】B
【解析】
【分析】
直接写出标准方程，即可得到答案.
【详解】
圆心在坐标原点，半径为2的圆的标准方程为.
故选：B
2．已知z为复数，且，则的取值范围是（ ）
A．B．C．D．
【答案】C
【解析】
【分析】
根据复数的几何意义可知复数z对应的点的轨迹是以原点O为圆心，以1为半径的圆，进而利用点与点之间的距离来求解.
【详解】
法一：在复平面内，复数z对应的点的轨迹是以原点O为圆心，以1为半径的圆，表示复平面内的点与点之间的距离.因为点与原点O的距离，所以的最小值是，最大值是，故的取值范围是.故选:C.
法二：因为复数z满足，不妨设，,则.因为，所以，所以的取值范围是.
故选:C.
3．已知双曲线的渐近线与圆相切，则a=（ ）
A．B．C．D．
【答案】B
【解析】
【分析】
先求得双曲线渐近线方程，根据直线与圆相切，可得圆心到直线的距离等于半径，列出方程，即可得答案.
【详解】
由题意得双曲线的渐近线方程为，根据对称性，不妨取，即，
因为渐近线与圆相切，
所以圆心（0,2）到直线的距离，解得，
所以或（舍）.
故选：B
4．已知直线 l 过点，则直线 l 被圆O：截得的弦长的最小值为（ ）
A．3B．6C．D．
【答案】B
【解析】
【分析】
由题可知当OA与直线 l 垂直时，所截得的弦长最短，利用弦长公式即得.
【详解】
依题意可知在圆内，且，圆O的半径为．
当OA与直线 l 垂直时，所截得的弦长最短，
即弦长的最小值为.
故选：B．
5．己知点，直线与圆相切于点，则的值为（ ）
A．B．C．D．
【答案】B
【解析】
【分析】
分析可得，，利用平面向量数量积的运算性质可求得结果.
【详解】
圆的标准方程为，圆心为，半径为，即，
由圆的几何性质可知，
所以，.
故选：B.
6．直线与圆相交，所得弦长为整数，这样的直线有（ ）条
A．10
B．9
C．8D．7
【答案】C
【解析】
【分析】
求出过定点的直线与圆的最短弦长为，最长的弦长为直径10，则弦长为6的直线恰有1条，最长的弦长为直径10，也恰有1条，弦长为7，8，9的直线各有2条，即可求出答案.
【详解】
直线过定点，圆半径为5，
最短弦长为，恰有一条，但不是整数；
弦长为6的直线恰有1条，有1条斜率不存在，要舍去；
最长的弦长为直径10，也恰有1条；
弦长为7，8，9的直线各有2条，共有8条，
故选：C．
7．若，分别为圆：与圆：上的动点，为直线上的动点，则的最小值为（ ）
A．B．6C．9D．12
【答案】C
【解析】
【分析】
设圆圆心半径为1，与关于直线对称，求出，最小时，由即可求解.
【详解】
易得圆圆心为半径为2，圆圆心为半径为1，设圆圆心半径为1，与关于直线对称，
则，解得，如图所示，要使最小，
则.
故选：C.
8．已知，为圆：上两点，且，点在直线：上，则的最小值为（ ）
A．B．
C．D．
【答案】A
【解析】
【分析】
先求得线段中点的轨迹，结合向量的模、圆与直线的位置关系等知识求得的最小值.
【详解】
设线段的中点为，
圆的圆心为，半径为.
到直线的距离为，
所以，故点的轨迹是以为圆心，半径为的圆，设点的轨迹为圆，
圆上的点到直线的最短距离为.
所以.
故选：A
9．【多选题】在平面直角坐标系中，已知圆：，则下列说法正确的是（ ）
A．若，则点在圆外
B．圆与轴相切
C．若圆截轴所得弦长为，则
D．点到圆上一点的最大距离和最小距离的乘积为
【答案】ABD
【解析】
【分析】
选项A，根据点与圆的位置关系判断即可；选项B，根据直线与圆相切的定义判断即可；选项C，根据圆的弦长公式求解即可；选项D，根据分和两种情况即可判断.
【详解】
对于A，因为时，将原点代入圆方程可得，故点在圆外，故A正确；
对于B，圆化为标准方程即为，则圆心，，
显然圆心到轴距离为等于半径，所以相切，故B正确；
对于C，对根据题意，，解得，解得所以圆截轴所得弦长为，
则，故C不正确；
对于D，当时，圆：，所以点在圆上，显然最小值为，最大值为，
故乘积且等于；当时，由选项A知，点在圆外，，
所以最大值为，最小值为，乘积为，故D正确.
故选：ABD.
10．方程表示圆，则的取值范围为______．
【答案】或
【解析】
【分析】
由方程表示圆得到不等式，直接求解即可.
【详解】
由题意知：，即，解得或.
故答案为：或.
11．已知直线与圆相交于两点，则=__________．
【答案】2
【解析】
【分析】
求出圆心到直线的距离，再利用弦长公式，求得弦长.
【详解】
根据圆的方程：，圆心坐标，半径，
∴圆心到直线距离，
所以，
故答案为：.
12．从圆外一点向圆引切线，则此切线的长为______．
【答案】2
【解析】
【分析】
作图，利用圆心到定点的距离、半径、切线长满足勾股定理可得.
【详解】
将圆化为标准方程：，则圆心，半径1，
如图，设，，切线长．
故答案为：2
13．已知平面上两定点A、B满足，动点P、Q分别满足，则的取值范围是___．
【答案】[－6,6]
【解析】
【分析】
令，由已知判断、的轨迹，再结合向量数量积的几何意义求的最值，即可得范围.
【详解】
若，
由题意知：在以为圆心，1为半径的圆上；在以为圆心，2为半径的圆上.
又，，则：
最大时，同向，此时，
最小时，反向，此时，
综上，的范围为[－6,6].
故答案为：[－6,6]
B组 能力提升
1．已知向量，，共面，且均为单位向量，，则的取值范围是（ ）
A．B．
C．D．
【答案】C
【解析】
【分析】
根据题意，求出的表达式，分析可得其表示单位圆上的点到定点的距离，由点与圆的位置关系分析可得答案
【详解】
因为向量，，共面，且均为单位向量，，
所以设，且，
所以，
所以，
所以其表示单位圆上的点到定点的距离，
所以其最大值为，最小值为，
所以的取值范围是，
故选：C
2．已知P是直线l：x＋y－7＝0上任意一点，过点P作两条直线与圆C：相切，切点分别为A，B.则｜AB｜的最小值为（ ）
A．B．C．D．
【答案】A
【解析】
【分析】
根据直线与圆相切的几何性质可知，当取得最小值时，最大，的值最小，当时，取得最小值，进而可求此时
【详解】
圆是以为圆心，2为半径的圆，由题可知，当最小时，的值最小. ，当取得最小值时，最大，最小，点到直线的距离，故当时，最大，且最大值为，此时，则.
故选：A
3．已知函数是偶函数，则f（x）的图象与y轴交点的纵坐标的最大值是（ ）.
A．6B．4C．2D．0
【答案】B
【解析】
【分析】
因为为二次函数，故为偶函数时，对称轴为，可求出和的关系，而图象与轴交点的纵坐标是，数形结合求最值即可.
【详解】
解：因为是偶函数，
所以，所以，即，，
所以是圆位于x轴上和上方的半圆上的点.
又因为，
即求的最大值，
令，则，它表示斜率为2的直线，
如图：
当直线过点时，
在直线在轴上的截距最小，从而最大，即
故选：B．
4．已知直线，若P为l上的动点，过点P作的切线，切点为A、B，当最小时，直线的方程为__________.
【答案】
【解析】
【分析】
由已知结合四边形面积公式及三角形面积公式可得，说明要使最小，则需最小，此时与直线垂直，写出所在直线方程，与直线的方程联立，求得点坐标，然后写出以为直径的圆的方程，再与圆的方程联立可得所在直线方程．
【详解】
解：的圆心，半径，
四边形面积，
要使最小，则需最小，
当与直线垂直时，最小，此时直线的方程为，
联立，解得，
则以为直径的圆的方程为，
则两圆方程相减可得直线的方程为．
故答案为：．
5．平面直角坐标系中，点、、，动点在的内切圆上，则的最小值为_________.
【答案】##
【解析】
【分析】
求出的内切圆方程，设点，计算得出，其中点，数形结合可求得的最小值.
【详解】
由两点间的距离公式可知，则是边长为的等边三角形，
设的内切圆的半径为，则，解得，
因为点、关于轴对称，所以，的内切圆圆心在轴上，
易知直线的方程为，原点到直线的距离为，
所以，的内切圆为圆，设点，
，其中点，
所以，，
当且仅当点为射线与圆的交点时，等号成立，故的最小值为.
故答案为：.
【点睛】
关键点点睛：解本题的关键在于分析出，再利用三点共线以及数形结合思想求得最值.
圆的标准方程
圆的一般方程
定义
在平面内，到定点的距离等于定长的点的集合叫圆，确定一个圆最基本的要素是圆心和半径
方程
圆心
半径
区别与
联系
（1）圆的标准方程明确地表现出圆的几何要素，即圆心坐标和半径长；
（2）圆的一般方程的代数结构明显，圆心坐标和半径长需要通过代数运算才能得出；
（3）二者可以互化：将圆的标准方程展开可得一般方程，将圆的一般方程配方可得标准方程
标准方程的形式
一般方程的形式
点（x0，y0）在圆上
点（x0，y0）在圆外
点（x0，y0）在圆内