河北省雄安新区2023-2024学年八年级下学期期末数学试题

这是一份河北省雄安新区2023-2024学年八年级下学期期末数学试题，共12页。试卷主要包含了答案须用黑色字迹的签字笔书写．等内容，欢迎下载使用。

2024.7
注意事项：
1.本试卷共6页，满分120分，考试时长120分钟．
2.答卷前将密封线左侧的项目填写清楚．
3.答案须用黑色字迹的签字笔书写．
一、选择题（本大题共12个小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1.若二次根式有意义，则的值不可以是（ ）
A.0 B.1 C.1.5 D.2
2.若函数是正比例函数，则的值为（ ）
A.-7 B.7 C.0 D.1
3.在中，，则的度数为（ ）
A. B. C. D.
4.下表记录了甲、乙、丙、丁四名学生最近三次三级跳远成绩的平均数与方差，根据表中数据，从中选择一名成绩好且发挥稳定的学生参加比赛，应选（ ）
A.甲 B.乙 C.丙 D.丁
5.以下列各组数为边长，不能构成直角三角形的是（ ）
A. B. C. D.
6.二十四节气是中国古代劳动人民长期经验积累的结晶，如图是一年中部分节气所对应的白昼时长示意图．在下列选项中自昼时长超过14小时的节气是（ ）
A.惊蛰 B.立夏 C.夏至 D.大寒
7.已知一次函数，且随着的增大而减小，则在平面直角坐标系内它的图象可能是（ ）
A. B.
C. D.
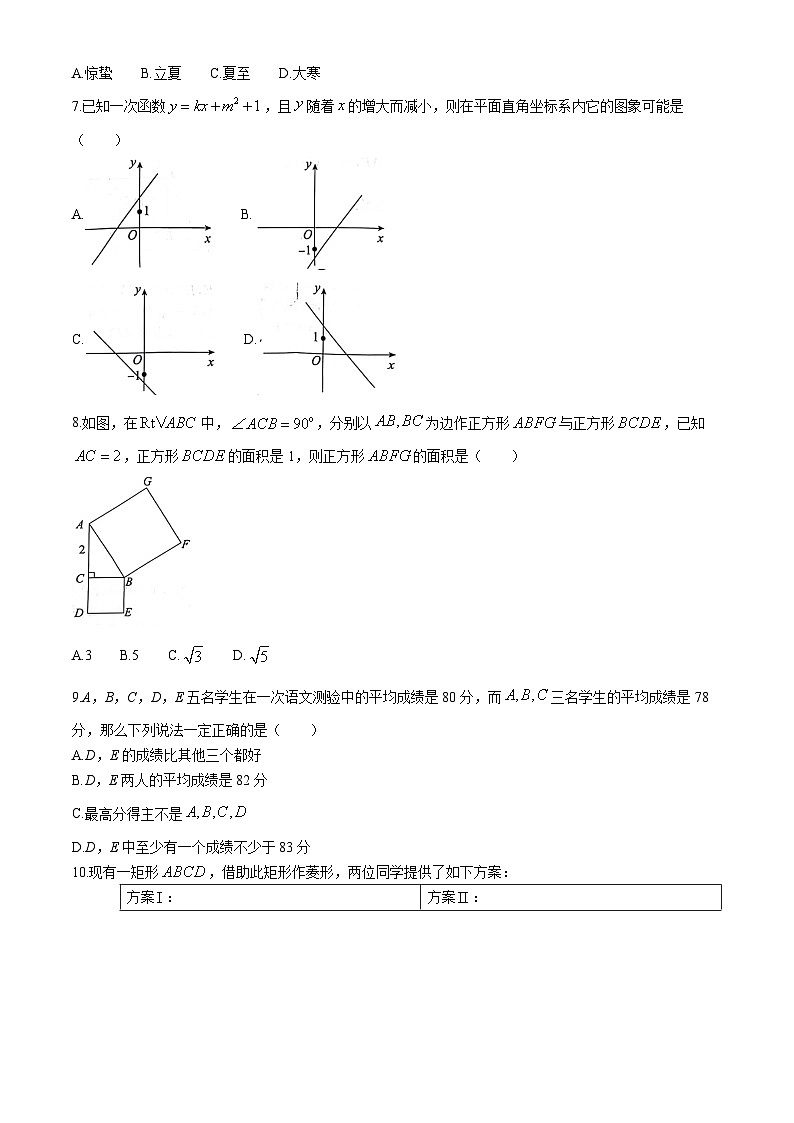
8.如图，在中，，分别以为边作正方形与正方形，已知，正方形的面积是1，则正方形的面积是（ ）
A.3 B.5 C. D.
9.A，B，C，D，E五名学生在一次语文测验中的平均成绩是80分，而三名学生的平均成绩是78分，那么下列说法一定正确的是（ ）
A.D，E的成绩比其他三个都好
B.D，E两人的平均成绩是82分
C.最高分得主不是
D.D，E中至少有一个成绩不少于83分
10.现有一矩形，借助此矩形作菱形，两位同学提供了如下方案：
对于方案，，说法正确的是（ ）
A.可行、不可行 B.不可行、可行
C.，都可行 D.，都不可行
11.某农科所利用大棚栽培技术培育一种优质瓜苗，这种瓜苗早期在农科所的温室中培养，生长到后移至大棚内，沿插杆继续向上生长到后，再移出大棚．研究表明：这种瓜苗生长的高度与生长的时间天）之间的关系大致如图所示，已知瓜苗生长到时开始开花结果．下列啃论不正确的是（ ）
A.这种瓜苗在温室打生长15天
B.这种瓜苗在大棚内生长的平均速度为每天长高
C.这种瓜苗在大棚内生长的时间比在温室中生长的时间多30天
D.这种瓜苗开花结果时，在大棚内生长的时间为30天
12.甲、乙、丙三位同学在探索下面这道题：
甲说：四边形是平行四边形；
乙说：若的面积为10，则菱形的面积为20；
丙说：有可能平分．
则下列说法正确的是（ ）
A.只有甲和乙正确 B.只有甲和丙正确
C.只有乙和丙正确 D.甲、乙、丙都正确
二、填空题（本大题共4个小题，每小题3分，共12分．其中第16小题第一个空2分，第二个空1分）
13.__________．
14.如图，在中，，则的长为__________．
15.如图，直线与直线相交于点，则关于的不等式的解集为__________．
16.如图，在四边形中，分别是的中点．
（1）若，则__________；
（2）若，则的度数为__________．
三、解答题（本大题共8个小题，共72分．解答应写出文字说明、证明过程或演算步骤）
17.（本小题满分8分）
计算：
（1）；
（2）．
18.（本小题满分8分）
为了加强心理健康教育，某校组织九年级（1）班和（2）班两个班的学生进行了心理健康常识测试（分数为整数，满分为10分），已知两班学生人数相同，根据测试成绩绘制了如图所示的统计图．
（1）求（2）班学生中测试成绩为10分的人数；
（2）请根据上面的信息求下表中的值．
19.（本小题满分8分）
有一块长方形木板，沿图中实线在木板上截出两个面积分别为和的正方形木板．
（1）分别求出原长方形木板的长和宽；
（2）求阴影部分长方形的面积．
20.（本小题满分8分）
如图，平行四边形的两条对角线与相交于点是线段上的两点，连接，已知．
（1）求证：四边形是平行四迌形．
（2）若，求证：四边形为菱形．
21.（本小题满分9分）
已知一次函数．
（1）补全表中自变量对应的函数值后，画出该函数的图象；
（2）若该一次函数的图象与轴交于点，与轴交于点，求的面积；
（3）求时的取值范围．
22.（本小题满分9分）
如图，一根直立的旗杆高，因刮大风，旗杆从点处折断，顶部着地且距离旗杆底部处．
（1）求旗杆在距地面多高处折断；
（2）工人在修复的过程中，发现在折断点的下方的点处，有一明显裂痕，若下次大风将旗杆从点处吹断，则距离旗杆底部周围多大范围内有被砸伤的危险？
23.（本小题满分10分）
共享电动车给我们的出行提供了方便．现有两种品牌的共享电动车，收费与骑行时间之间的函数关系如图所示，其中品牌的收费方式对应品牌的收费方式对应．
（1）B品牌共享电动车骑行10分钟后，每分钟收费__________元．
（2）当时，与的函数关系式为__________．
（3）如果小明每天早上需要骑行品牌或品牌的共享电动车去工厂上班，已知两种品牌共享电动车的平均行驶速度均为，小明家到工厂的距离为，那么小明选择哪个品牌的共享电动车更省钱？可以省多少？
24.（本小题满分12分）
如图1，四边形为正方形，为对角线上一点，且不与点重合，连接．
（1）求证：．
（2）如图2，过点作，交边于点，以为邻边作矩形，连接．
①求证：矩形是正方形；
②若正方形的边长为，求正方形的边长．
2023—2024学年第二学期期末学业质量监测
八年级数学参考答案及评分参考（人教版）
2024.7
一、选择题（本大题共12个小题，每小题3分，共36分）
二、填空题（本大题共4个小题，每小题3分．共12分．其中第16小题第一个空2分，第二个空1分）
13. 14. 15. 16.（1）；（2）．
三、解答题（本大题共8个小题，共72分）
17.解：（1）
（2）
18.解：（1）由题意知，（1）班和（2）班人数相等，
均为（人），
（2）班学生中测试成绩为10分的人数为：6（人）．
答：（2）班学生中测试成绩为10分的人数是6.
（2）由题意知，（2）班学生测试成绩的平均数为：
（分）．
由统计图可得，扇形统计图中9分的人数占，占比最多，条形统计图中第25，26个数均为8分，
（2）班学生测试成绩的众数为9分，（1）班学生测试成绩的中位数为8分，
．
19.解：（1）由题意得，原长方形的长为，
原长方形的宽为．
答：原长方形木板的长是，宽是．
（2）由题意得，阴影部分长方形的宽为，
长为，
阴影部分长方形的面积是．
20.证明：（1）四边形是平行四边形，
，
．
在和中，
（），
，
，
即，
四边形是平行四边形．
（2）四边形是平行四边形，，
平行四边形是菱形，
．
由（1）可知，四边形是平行四边形，
平行四边形是菱形．
21.解：（1）补全表格如下：
描点、连线，画出函数图象，如图所示．
（2）当时，，
解得，
点的坐标为．
当时，，
点的坐标为，
的面积．
（3）当时，．
当时，．
随的增大而增大，
当时，的取值范围是．
22.解：（1）由题意可知，，设，则．
，
，即，解得，
，
故旗杆在距地面3米处折断．
（2）如图，若大风将旗杆从点处吹断，旗杆顶部落到处．
点距地面的高度为，
，
，
距离旗杆底部周围范围内有被砸伤的危险．
23.解：（1）0.2
（2）
（3）（min）．
设品牌的费用为，且图象过，
，
解得，
，
当时，品牌的费用为，
B品牌的费用为．
，且（元），
小明选择品牌的共享电动车更省钱，可以省元．
24.（1）证明：四边形为正方形，
．
在和中，
（SAS），
．
（2）①证明：如图1，作于于，得到矩形，
．
点是正方形对角线上的点，
．
，
．
在和中，
（ASA），
．
四边形是矩形，
矩形是正方形．
②解：连接，如图2.
正方形和正方形．
，
在和中，
（），
．
，
，
，
．
，
，
，
正方形的边长为．甲
乙
丙
丁
平均数（米）
13
12
13
10.5
方差
3.2
3.2
7.8
7.5
方案：
分别取边的中点，顺次连接这四点，围成的四边形即为所求．
方案：
连接，作的垂直平分线分别交于点，连接，四边形即为所求．
如图，菱形中，与相交于点，延长至，使得，连接和．
统计量
平均数
众数
中位数
（1）班
8
8
（2）班
8
0
1
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
C
A
B
C
D
B
D
C
D
A
0
1
4
6