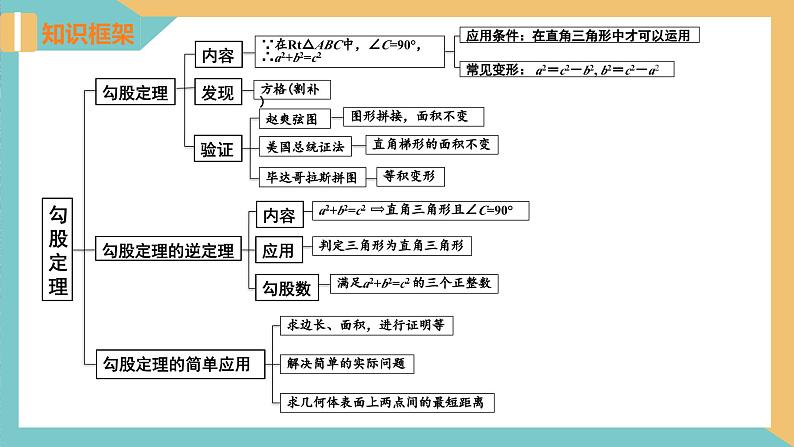
初中数学3.1 勾股定理复习ppt课件

这是一份初中数学3.1 勾股定理复习ppt课件，共38页。PPT课件主要包含了学习目标，勾股定理，方程思想，分类讨论思想，数形结合思想，北偏东50°，连接AC，x24，折叠问题，最短路径问题等内容，欢迎下载使用。

2. 体会数形结合思想、方程思想、分类讨论思想和转化思想在解决问题中的作用.
1. 进一步理解并掌握勾股定理和勾股定理的逆定理，能用勾股定理和逆定理解决一些实际问题；
∵在Rt△ABC中，∠C=90°，∴a2+b2=c2
判定三角形为直角三角形
满足a2+b2=c2 的三个正整数
求边长、面积，进行证明等
求几何体表面上两点间的最短距离
应用条件：在直角三角形中才可以运用
常见变形： a2＝c2－b2, b2＝c2－a2
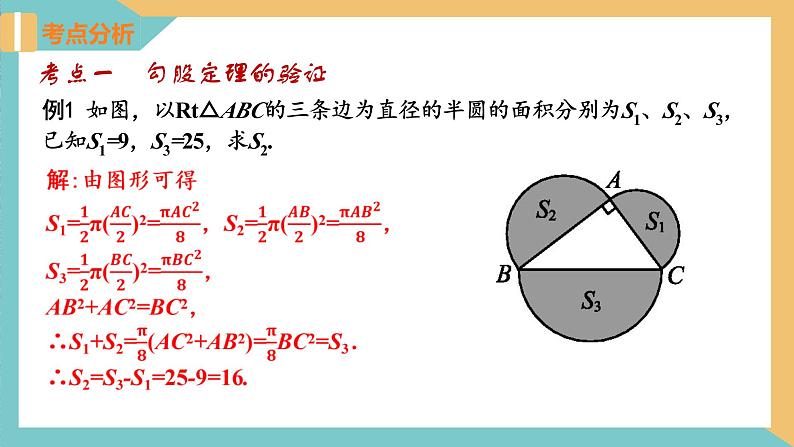
例1 如图，以Rt△ABC的三条边为直径的半圆的面积分别为S1、S2、S3，已知S1=9，S3=25，求S2.
考点一 勾股定理的验证
1.（2021·山西）在勾股定理的学习过程中，我们已经学会了运用以下图形，验证著名的勾股定理：这种根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明”．实际上它也可用于验证数与代数，图形与几何等领域中的许多数学公式和规律，它体现的数学思想是（     ）A．统计思想 B．分类思想 C．数形结合思想 D．函数思想
2.（2022·贵州）如图，“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形，若图中的直角三角形的两条直角边的长分别为1和3，则中间小正方形的周长是（ ）A．4 B．8 C．12 D．16
3.（2022·四川）“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第六代勾股树中正方形的个数为 __．
解:∵第一代勾股树中正方形有1+2=3（个），第二代勾股树中正方形有1+2+22=7（个），第三代勾股树中正方形有1+2+22+23=15（个），．∴第六代勾股树中正方形有1+2+22+23+24+25+26=127（个）.
4.（2021·四川）如图是“弦图”的示意图，“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的，它标志着中国古代的数学成就．它由4个全等的直角三角形与一个小正方形组成，恰好拼成一个大正方形，每个直角三角形的两条直角边分别为a、b，斜边为c．请你运用此图形证明勾股定理：a2+b2＝c2．
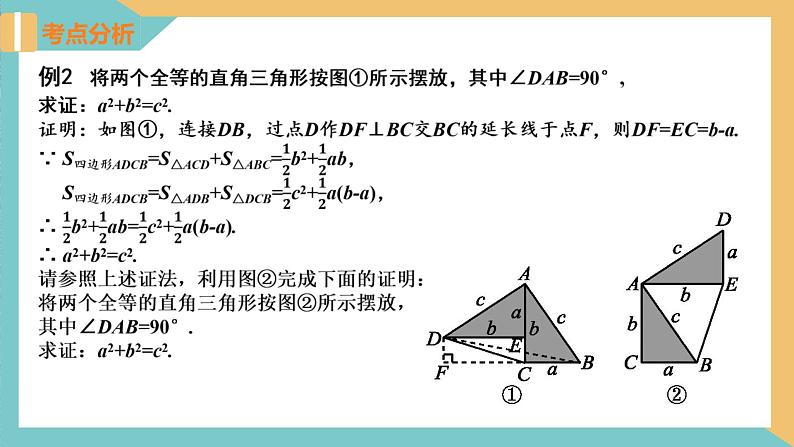
5.勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小明以灵感，他惊喜地发现，当四个全等的直角三角形按图所示摆放时，可以用“面积法”来验证勾股定理.，请你写出推导过程.
考点二 勾股定理
例1 在Rt△ABC中，∠ACB=90°，CD⊥AB于D，AC=20，BC=15.（1）求AB的长；（2）求BD的长．
解：（1）∵在Rt△ABC，∠ACB=90°，
由勾股定理得：AB2=AC2+BC2=202+152=252，∴AB=25.
（2）设BD=x，则AD=25-x.
∵AC2-AD2=CD2，BC2-BD2=CD2，
∴AC2-AD2=BC2-BD2，
∴202-(25-x)2=152-x2，即50x=450，
解得x=9. ∴BD=9.
两直角三角形共一边的情况，可利用勾股定理列方程求解.
例2 在△ABC中，AB=20，AC=13，高AD=12，求△ABC的面积.
1.（2021·山东）在Rt△ABC中，若∠C=90°，AC=3，BC=4，则点C到直线AB的距离为（      ）A. 3 B. 4 C. 5 D. 2.4
2. Rt△ABC中，斜边AB=2，则AB2+AC2+BC2的值为（　　）A. 8 B. 4 C. 6 D.无法计算
3. 一直角三角形的三边分别为2、3、x，那么以x为边长的正方形的面积为_________.
4. 如图，∠C=∠ABD=90°，AC=3，BC=4，BD=12，则AD的长为______．
5.如图，在△ABC中，∠C=90°，AB=8，D是BC上一点，AD=BD=5，求CD的长.
解：∵∠C=90°,∴△ACD和△ABC都是直角三角形.在Rt△ACD中，∵AC2+CD2=AD2，∴AC2=AD2-CD2.在Rt△ABC中，∵AC2+BC2=AB2，∴AC2=AB2-BC2.∴AD2-CD2=AB2-BC2.设CD=x，则BC=5+x，∴52-x2=82-(5+x)2，解得x=1.4.∴CD的长为1.4.
考点三 勾股定理的逆定理
例1 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫格点，已知网格中有以格点A、B、C为顶点的△ABC，请你根据所学的知识回答下列问题:(1)求△ABC的面积;(2)判断△ABC的形状，并说明理由.
例2（2021·广西）如图，某港口P位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行12海里和16海里，1小时后两船分别位于点A、B处，且相距20海里，如果知道甲船沿北偏西40°方向航行，则乙船沿____________方向航行．
解：由题意得：AP=1×12=12海里，PB=1×16=16海里，AB=20海里，∴AP2+BP2=400=AB2，∴∠APB=90°，∵∠APN=40°，∴∠BPN=50°，∴乙船沿北偏东50°(或东偏北40°)方向航行.
1. (2018·江苏南通)下列各组线段能构成直角三角形的一组是（ ）A．3，4，5 B．2，3，4 C．4，6，7 D．5，11，12
2.下列各组数是勾股数的是 （　 ） A. 6，8，10 B. 7，8，9C. 0.3，0.4，0.5 D. 52，122，132
4. △ABC的三边长分别是a、b、c，且a＝n2－1，b＝2n，c＝n2＋1．问：△ABC是直角三角形吗？证明你的结论.
解：∵AB²+BC²=(n²-1)²+(2n)² =n4 -2n²+1+4n² =n4 +2n²+1 =(n²+1)² =AC²，∴ 由勾股定理的逆定理得△ABC直角三角形，边AC所对的角是直角.
5. 如图是由边长为1的小正方形组成的网格.(1) 你能判断AD与CD的位置关系吗？说出你的理由.(2) 求四边形ABCD的面积.
∵ AD2=1+4=5，CD2=4+16=20 ，AC= 5
∴ AD2+CD2＝25，AC2＝25
∴ AD2+CD2＝AC2
∴ 由勾股定理的逆定理得：∠CAD＝90°. ∴ AD⊥CD
(2) S四边形ABCD=S△ADC+S△ABC
例1（2021·江苏宿迁）《九章算术》中有一道“引葭赴岸”问题：“仅有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问水深，葭长各几何？”题意是：有一个池塘，其地面是边长为10尺的正方形，一棵芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B'(示意图如图)，则水深为________尺．
解：如图，设水池的水深AC为x尺，则这根芦苇长AB'=AB=(x+1)尺，
Rt△AB'C中，B'C=5尺，
由勾股定理得：B'C2+AC2=AB'2，
即 52+ x2= (x+1)2
25+ x2= x2+2x+1，
∴ x=12. ∴AC=12尺.
答：水池的水深12尺，这根芦苇长13尺.
考点四 勾股定理的简单应用
例2 如图，在长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，求△ABE的面积.
例3 如图所示，已知长方体的长为2 cm，宽为1 cm，高为4 cm. 一只蚂蚁如果沿该长方体的表面从点A爬到点C'处吗，那么沿哪条路径爬行最近?最短路程为多少?
解：如图①AC' 2=AC2+CC' 2=(2+1)2+42=25.
如图②AC' 2=AB2+BC' 2=22+(4+1)2=29.
如图③AC' 2=AD2+DC' 2=12+(4+2)2=37.
综上所述，最短路径应为如图①所示的线段AB'. ∵AC'2=25，∴AC'=5(cm)吗，即最短路程为5 cm.
1. 如图，有两颗树，一颗高10米，另一颗高4米，两树相距8米．一只鸟从一颗树的树梢飞到另一颗树的树梢，问小鸟至少飞行（ ）A．8米 B．10米 C．12米 D．14米
2.（2020·江苏扬州·中考真题）《九章算术》是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架．如图所示是其中记载的一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：一根竹子原高1丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？答：折断处离地面________尺高．
3.（2021·四川）如图，△ABC中，∠ACB=90°，AC=8，BC=6，将△ADE沿DE翻折，使点A与点B重合，则CE的长为（     ）
4. 如图，∠AOB=90°，OA=9 m，OB=3 m，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿BC方向匀速前进拦截小球，恰好在点C处截住了小球. 如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少?
解：∵小球滚动的速度与机器人行走的速度相等，运动时间相等，∴BC=AC.设BC=AC=x m，则OC=(9-x)m.由勾股定理，得OB2+OC2=BC2,即32+(9-x)2=x2，解得x=5. ∴机器人行走的路程BC是5 m.
5.台风是一种自然灾害，以台风中心为圆心在周围上千米的范围内形成极端气候，有极强的破坏力. 如图，有一台风中心沿东西方向由点A向点B移动，已知点C为一海港，且点C与点A、B的距离分别为300 km和400 km. AB=500 km，以台风中心为圆心周围250 km以内为受影响区域.(1)海港C会受台风影响吗?为什么?
解：(2)如图，当EC=FC=250 km时，台风正好影响海港C.根据勾股定理，得ED2=EC2-CD2=2502-2402=4900,∴ED=70(km).∴EF=2ED=140 km.∵台风的速度为20 km/h,∴140÷20=7(h),即台风影响该海港持续的时间为7 h.
(2)若台风的速度为20 km/h，台风影响该海港持续的时间有多长?
例1 如图，在四边形ABCD中，AB=20cm，BC=15cm，CD=7cm，AD=24cm，∠ABC=90°．猜想∠A与∠C关系并加以证明．
解：猜想∠A+∠C=180°．连接AC.∵∠ABC=90°，∴在Rt△ABC中，由勾股定理得 AC2=AB2+BC2=202+152=252∵AD2+DC2=242+72=625=252=AC2，∴△ADC是直角三角形，且∠D=90°，∵∠DAB+∠B+∠BCD+∠D=360°，∴∠DAB+∠BCD=180°，即∠A+∠C=180°．
考点五 勾股定理和勾股定理的逆定理综合应用
例2 有一块空白地，如图，∠ADC=90°，CD=6 m，AD=8 m，AB=26 m，BC=24 m．试求这块空白地的面积．
解：连接AC.在Rt△ADC中，
∵AC2=AD2+CD2（勾股定理） =82+62=100，
∵AC2+BC2=102+242=676=262=AB2，
∴△ACB为直角三角形(勾股定理的逆定理).
∴S空白部分=S△ACB-S△ACD
1.如图，AD⊥BC，垂足为D. 如果CD=1，AD=2，BD=4，那么∠BAC是直角吗？请说明理由.
解：∵AD⊥BC，∴∠ADC=∠ADB=90°.∴ 在Rt△ADC中，AC2=AD2+DC2=22+12=5. 在Rt△ADB中，AB2=AD2+BD2=22+42=20.∵AC2+AB2=20+5=25，BC2=52=25.∴AC2+AB2=BC2.∴△ABC直角三角形，∠BAC=90°.
2. 在△ABC中，D为BC边上的点.已知AB=13，AD=12，AC=15，BD=5，求DC的长.
解：∵AB=13，AD=12，BD=5，∴ AB2=AD2+BD2.∴ 由勾股定理的逆定理得：△ABD是直角三角形，且∠ADB=90°.∴∠ADC=90°.在Rt△ADC中，AC2=AD2+DC2. ∵AD=12，AC=15,∴DC2=AC2-AD2=152-122=92.∴ DC=9.
3. 如图，四边形ABCD是学校的一块空地，经数学兴趣小组的测量可知，∠B=90°，BC=3米，AB=4米，CD=13米，AD=12米．为了提高校园的绿化面积，现学校决定在空地内铺草坪，若铺设每平方米草坪需要30元，则将这块空地全部铺满一层草坪的费用是多少？
4. 做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱，一根长为70厘米的木棒能否放入，为什么？试用今天学过的知识说明．