北师大版七年级下册1 同底数幂的乘法示范课课件ppt

这是一份北师大版七年级下册1 同底数幂的乘法示范课课件ppt，共21页。PPT课件主要包含了学习目标，忆一忆，×103，16个10，3个10，19个10，1016+3，乘方的意义，乘法的结合律，议一议等内容，欢迎下载使用。

1.理解并掌握同底数幂的乘法法则.（重点） 2.能够运用同底数幂的乘法法则进行相关计算.（难点）
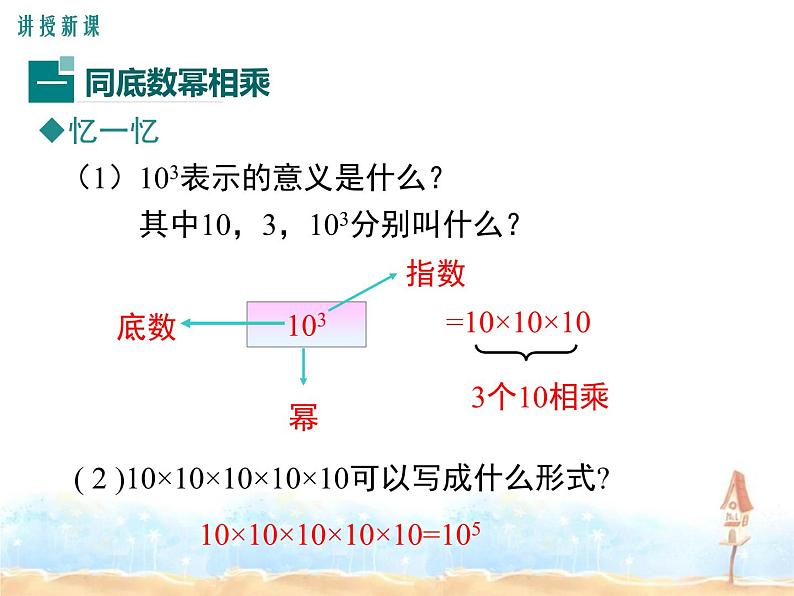
（1）103表示的意义是什么？ 其中10，3，103分别叫什么？
( 2 )10×10×10×10×10可以写成什么形式?
10×10×10×10×10=105
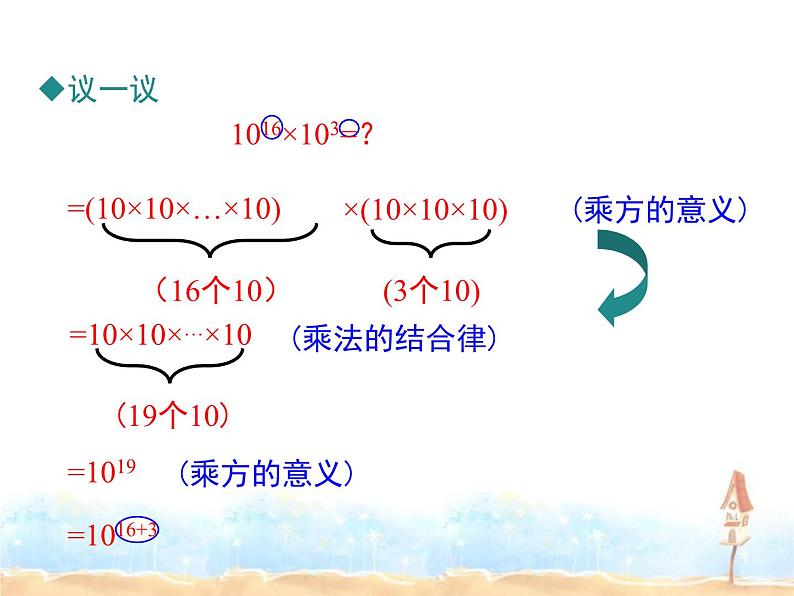
=(10×10×…×10)
×(10×10×10)
=10×10×…×10
（1）25×22=2 （ ）
1.根据乘方的意义填空，观察计算结果，你能发现 什么规律？
=(2×2×2×2×2)
=2×2×2×2×2× 2×2
（2）a3·a2=a（ ）
=(a﹒a﹒a) (a﹒a)
5m× 5n =5（ ）
2.根据乘方的意义填空，观察计算结果，你能发现 什么规律？
=(5×5×5×…×5)
×(5×5×5 ×…×5)
am · an =a（ ）
如果m,n都是正整数，那么am·an等于什么？为什么？
( 个a)
=a( )
am · an = am+n (m，n都是正整数).
底数　 ，指数　 .
1.计算a6 • a2的结果是( )A.a3 B.a4 C.a8 D.a122.计算（-a2）• a5所得的结果是( )A.a7 B.-a7 C.a10 D.-a103.计算：（1）93×96= _____；（2）（-3）7×（-3）3=_____ .（写为幂的形式）
判断（正确的打“√”，错误的打“×”）
(1)x4·x6=x24 ( 　) （2） x·x3=x3 ( 　)(3) x4+x4=x8 (　 ) (4) x2·x2=2x4 (　 )(5)(－x)2 · (－x)3 = (－x)5 (　 ) (6)a2·a3－ a3·a2 = 0 ( 　 ) (7)x3·y5=(xy)8 ( 　 ) (8) x7+x7=x14 ( 　 )
对于计算出错的题目，你能分析出错的原因吗？试试看！
a · a6 · a3
类比同底数幂的乘法公式am · an = am+n (当m、n都是正整数)
= a7 · a3 =a10
例题2：计算下列算式①53×54×56； ②③y3 • y5 • y2 • y3； ④3n • （-3）5 • 3n(n是正整数).
（1）把下列各式化成（x-y）n的形式： ①（x-y）•（x-y）3 •（x-y）2； ②（x-y）3 •（y-x）2 •（y-x）； ③（x-y）•（x-y）4 •（y-x）3.
【点拨】相反数的偶数次幂相等，相反数的奇数次幂互为相反数，即（a-b）2n=（b-a）2n，（a-b）2n+1=-（b-a）2n+1(n为正整数).
解：①原式=（x-y）1+3+2=（x-y）6.②原式=-（x-y）3•（x-y）2•（x-y）=-（x-y）3+2+1=-（x-y）6.③原式=-（x-y）•（x-y）4•（x-y）3=-（x-y）1+4+3=-（x-y）8.
同底数幂的乘法法则逆运算：
am+n = am · an (m，n都是正整数).
例题（1）已知an－3·a2n+1=a10,求n的值;
例题（2）已知xa=2,xb=3,求xa+b的值.
公式逆用：am+n=am·an
公式运用：am·an=am+n
解：n－3+2n+1=10, n=4;
解：xa+b=xa·xb=2×3=6.
1.计算：（1）（x+y）3 •（x+y） •（x+y）2=_________；（2）（x-y）5 •（y-x）3 •（x-y）=___________.2.若a4 • a2m-1=a11，则m=_______.3.已知xa+b • x2b-a=x9，求（-3）b+（-3）3的值.
解：因为xa+b • x2b-a=x9，所以a+b+2b-a=9，解得b=3.所以（-3）b+（-3）3=（-3）3+（-3）3 =2×（-3）3 =2×（-27） =-54.
4、若8×4=2x，则x=( ).