北师大版七年级上册数学 2.12用计算器进行运算-课件PPT

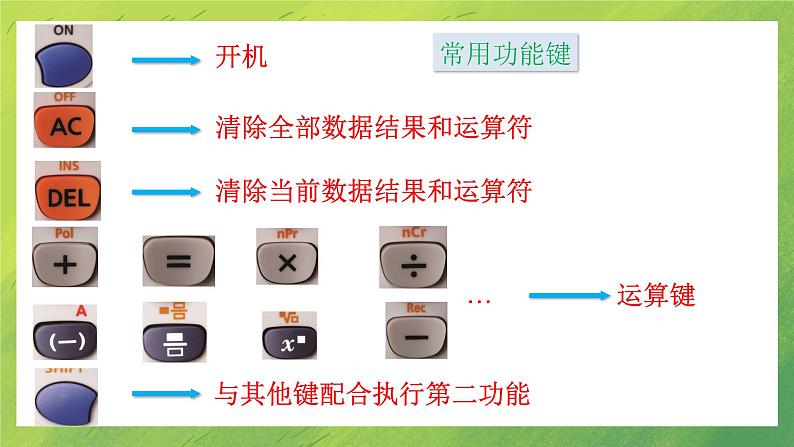
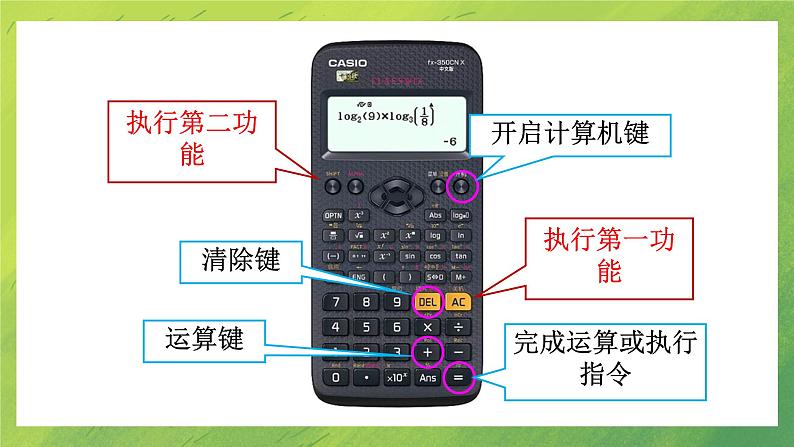
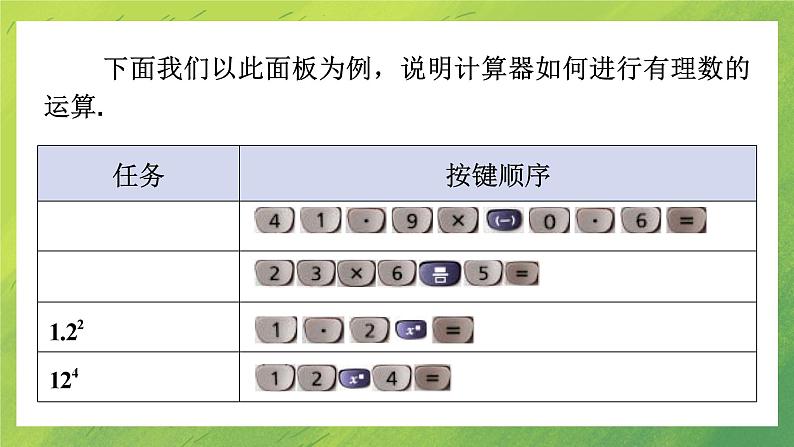
LOGO北师大版 数学 七年级 上册2.13 用计算器进行运算导入新知 观察右图中展示的计算器，试着摸索各个按键的功能.素养目标1.会使用计算器进行有理数的加、减、乘、除、乘方运算及其混合运算.2.能运用计算器解决实际问题中的复杂运算.3.经历运用计算器探求规律的活动,发展合情推理能力.认识科学计算器：右图是一种科学计算器的面板.显示器键盘开机清除全部数据结果和运算符 清除当前数据结果和运算符 运算键与其他键配合执行第二功能…常用功能键开启计算机键清除键完成运算或执行指令运算键执行第一功能执行第二功能 下面我们以此面板为例，说明计算器如何进行有理数的运算.1.计算器上的 DEL 键的功能是 (　 　)　　　　 　　　　　　　　　　A.开启计算器B.关闭计算器C.清除当前显示的内容D.计算乘方C2.用计算器计算35+12,按键顺序正确的是(　 　)①依次按 35 数字键;②依次按 12 数字键;③按 + 键;④按 = 键.A.①②③④ B.①③②④C.①④②③ D.①③④②B B4.用计算器计算129,按键顺序正确的是 (　 　)D5.小芳在用计算器计算“-14.9×73”时,发现计算器的小数点键坏了,你还能用这个计算器把正确的结果算出来吗?请把你想到的方法用算式表示出来: . -149÷10×73(答案不唯一)6.若按键顺序是 ,则表示的运算式子是 ,计算出的结果是 . -53+1　-1247.有一张厚度是0.1 mm的纸,假设我们能将它连续对折30次,这时它的厚度能超过珠穆朗玛峰的海拔(8 844.43 m)吗?请用计数器帮你得出答案.0.1×230 mm=107 374 182.4 mm=107 374.182 4 m>8 844.43 m.答:将一张厚度是0.1 mm的纸连续对折30次后,它的厚度能超过珠穆朗玛峰的海拔(8 844.43 m).8.某公司以81 710 000元的价格中标我市城市轨道交通6号线工程,81 710 000用科学记数法精确到1 000 000,可表示为 (　 　)A.8.1×107 B.8.1×108C.8.2×107 D.8.2×108C用科学记数法表示一个数的近似数时,一般先利用四舍五入法按精确度取近似值,再将近似值用科学记数法表示.观察下列语句中的数据，试着发现它们的不同之处.参加今天会议的有513人.约有五百人参加了今天的会议.确切反映实际人数.只是接近实际人数.定义：能够确切反映实际情况的数据叫做准确数, 表示与实际数据有差异的数据叫做近似数.宇宙现在的年龄约为200亿岁长江长约6300km圆周率约为3.14近似数近似数近似数例 按括号内的要求，用四舍五入法对下列各数取近似数：（1）0.0158（精确到0.001）；（2）304.35（精确到个位）；（3）1.804（精确到0.1）； （4）1.804（精确到0.01）．（4）1.804≈1.80．解：（1）0.0158 ≈0.016；（2）304.35≈304； （3）1.804 ≈1.8；方法点拨：判定精确程度的方法:在说明一个数的精确度时,主要看最后一个有效数字所在的数位,在哪一位就说成精确到哪一位.按要求对3.14159分别取近似数,下面结果错误的是( )A.3.1(精确到0.1)B.3.14(精确到0.01)C.3.141(精确到0.001)D.3.1416(精确到0.0001)C1.用计算器计算：(1)(-7)3; (2)134.=)(-)(＜73显示结果为：-343.=)(-)(＜14显示显示结果为：28561.32.下面数据中,是准确数的是( )A.珠穆朗玛峰高出海平面约8844米B.人的大脑有10000000000个细胞C.小明买了5本小说D.有关部门预测,到2020年轿车的拥有率将达到30%C3.由四舍五入法得到的近似数是3.75,下面的数中不可能是原数的是( )A.3.7514 B.3.7493 C.3.7504 D.3.755D4.下列说法中,正确的是( )A.近似数2.4万精确到万位 B.近似数24000精确到千位C.近似数2.4×104精确到千位 D.近似数2.4万精确到0.1C5.近似数2.70所表示的准确数a的范围是( )A.2.695≤a＜2.705 B.2.65≤a＜2.75C.2.695＜a≤2.705 D.2.65＜a≤2.75A用四舍五入法对下列各数按要求取近似数：(1)8.026(精确到0.01)；(2)549.49(精确到个位)；(3)999653(精确到千位)；(4)3.09×104(精确到千位).(4)3.09×104≈3.1×104.解：(1)8.026≈8.03；(2)549.49≈549；(3)999653≈1.000×106；使用计算器计算下列各式：1×9+2=12×9+3=123×9+4=1 234×9+5=…123 456 789×9+10=通过计算，你发现了什么规律？解： 1×9+2=11， 12×9+3=111， 123×9+4=1 111， 1 234×9+5=11 111， … 123 456 789×9+10=1 111 111 111， 发现1×9+2的结果是两个1组成的数， 12×9+3是由三个1组成的三位数…… 123 456 789×9+10的结果是由10个1组成的十位数．用计算器进行运算计算器的认识与使用近似数课堂小结表示与实际数据有差异的数据叫做近似数能够确切反映实际情况的数据叫做准确数