2024年中考数学压轴题精选专项突破-几何综合

这是一份2024年中考数学压轴题精选专项突破-几何综合，共34页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．如图，在△ABC中，∠ABC=60°，AB=8，BC=43，点D为边AC上一点，点F在BC的延长线上，BC=2CF．若四边形DCFE是平行四边形，连接AE，BE，则图中阴影部分的面积为（ ）
A．24B．12C．8D．6
2．如图，已知△ABO的顶点A和AB边的中点C都在双曲线y=4x（x＞0）的一个分支上，点B在x轴上，CD⊥OB于D，则△AOC的面积为（ ）
A．2B．3C．4D．32
3．如图，点E是△ABC的内心，连接AE并延长交BC于点F，交△ABC的外接圆于点D，连接BD．以下结论：①AE平分∠BAC；②BD=DC；③∠DBC=∠BAD；④BD=DE；⑤DE2=DF⋅DA，其中正确的结论有（ ）
A．2个B．3个C．4个D．5个
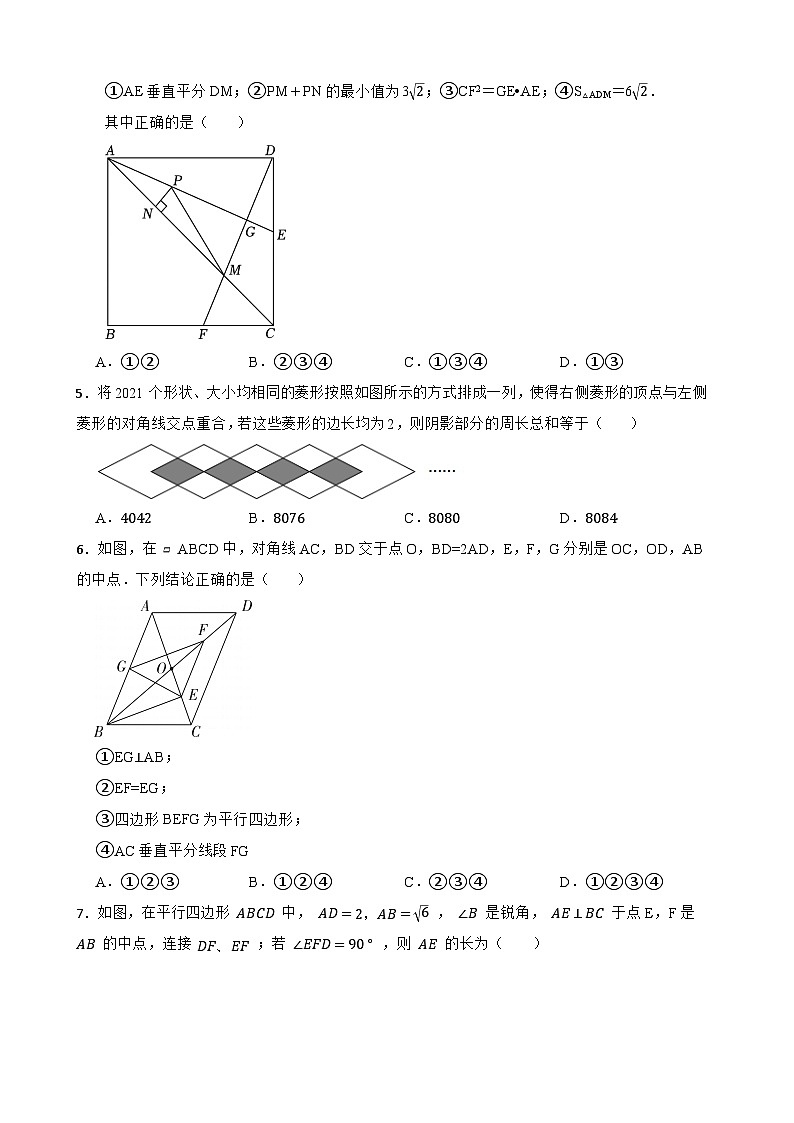
4．如图，正方形ABCD的边长为4，点E，F分别在边DC，BC上，且BF＝CE，AE平分∠CAD，连接DF，分别交AE，AC于点G，M．P是线段AG上的一个动点，过点P作PN⊥AC，垂足为N，连接PM．有下列四个结论：
①AE垂直平分DM；②PM＋PN的最小值为32；③CF2＝GE•AE；④S△ADM＝62．
其中正确的是（ ）
A．①②B．②③④C．①③④D．①③
5．将2021个形状、大小均相同的菱形按照如图所示的方式排成一列，使得右侧菱形的顶点与左侧菱形的对角线交点重合，若这些菱形的边长均为2，则阴影部分的周长总和等于（ ）
A．4042B．8076C．8080D．8084
6．如图，在 ▱ ABCD中，对角线AC，BD交于点O，BD=2AD，E，F，G分别是OC，OD，AB的中点．下列结论正确的是（ ）
①EG⊥AB；
②EF=EG；
③四边形BEFG为平行四边形；
④AC垂直平分线段FG
A．①②③B．①②④C．②③④D．①②③④
7．如图，在平行四边形 ABCD 中， AD=2，AB=6 ， ∠B 是锐角， AE⊥BC 于点E，F是 AB 的中点，连接 DF、EF ；若 ∠EFD=90∘ ，则 AE 的长为（ ）
A．2B． 5C．322D． 332
8．如图，已知矩形ABCD的边长分别为a，b，进行如下操作：第一次，顺次连接矩形ABCD各边的中点，得到四边形 A1B1C1D1 ；第二次，顺次连接四边形 A1B1C1D1 各边的中点，得到四边形 A2B2C2D2 ；…如此反复操作下去，则第n次操作后，得到四边形 AnBnCnDn 的面积是（ ）
A．ab2nB．ab2n−1C．ab2n+1D．ab22n
9．嘉嘉同学遇到这样一道题：“如图，正方形 ABCD 中， P 是对角线 BD 上一点， PE⊥BC 于点 E ， PF⊥CD 于点 F ，连接 AP ， EF ．”关于这道题有下列说法：①四边形 PECF 是矩形；②AP=EF ；③PD=AD ；④AP⊥EF ，其中正确的说法是（ ）
A．①②③B．①②④C．①③④D．②③④
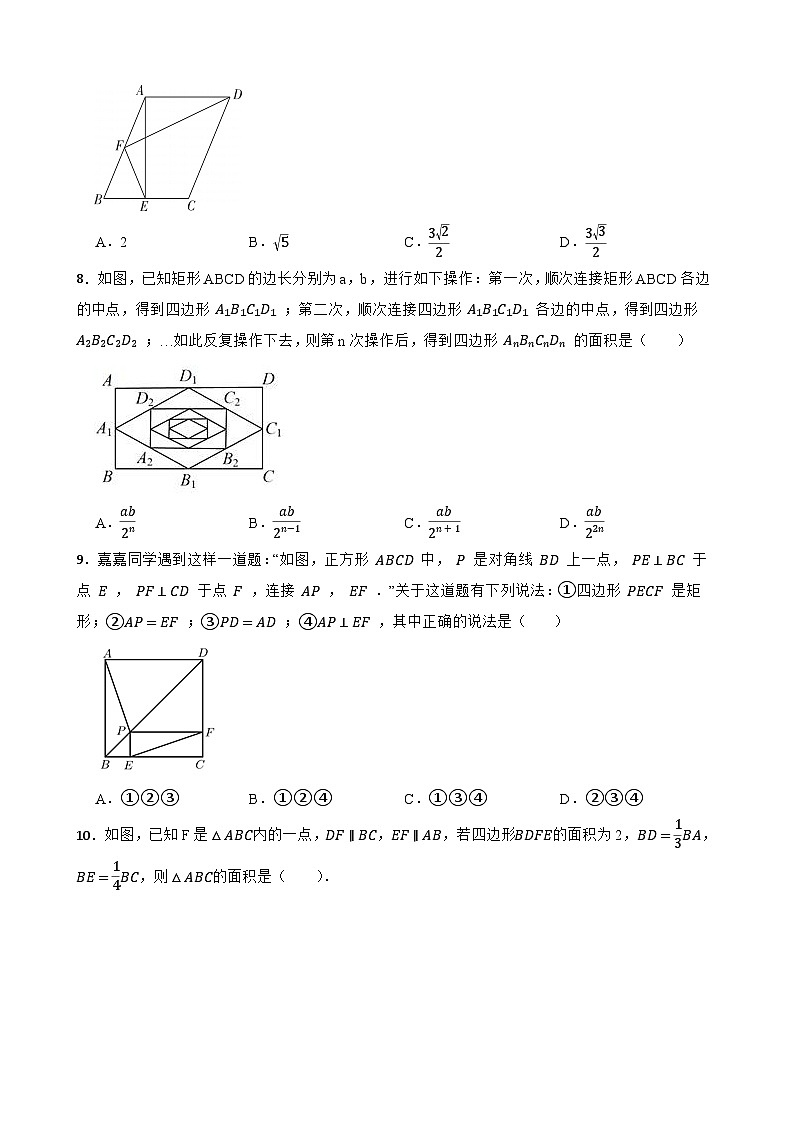
10．如图，已知F是△ABC内的一点，DF∥BC，EF∥AB，若四边形BDFE的面积为2，BD=13BA，BE=14BC，则△ABC的面积是（ ）．
A．6B．8C．10D．12
11．如图，在 ΔABC 中， AB=AC=5，BC=45 ， D 为边 AC 上一动点（ C 点除外），把线段 BD 绕着点 D 沿着顺时针的方向旋转90°至 DE ，连接 CE ，则 ΔCDE 面积的最大值为（ ）
A．16B．8C．32D．10
12．如图，在矩形ABCD中，AB=4，BC=3，将△BCD沿射线BD平移a个单位长度（a>0）得到△B'C'D'，连接AB'，AD'，则当△AB'D'是直角三角形时，a的值为（ ）
A．75或165B．2或165C．85或165D．75或3
二、填空题
13．如图1，有一张矩形纸片ABCD，已知AB=10，AD=12，现将纸片进行如下操作：现将纸片沿折痕BF进行折叠，使点A落在BC边上的点E处，点F在AD上（如图2），则DF= ；然后将△FBE绕点F旋转到△FMN，当MN过点C时旋转停止，则EN的长度为 ．
14．如图，边长为3的等边三角形ABC中，点M在直线BC上，点N在直线 AC 上，且∠BAM＝∠CBN，当BM＝1时， AN= ．
15．如图，已知双曲线 y=kx (k>0) 经过Rt△OAB的斜边OB的中点D，与直角边AB相交于点C．当 BC⋅OA=6 时， k= ．
16．如图，矩形ABCD的面积为5，它的两条对角线交于点O1，以AB，AO1为两邻边作平行四边形ABC1O1，平行四边形ABC1O1的对角线交于点O2，同样以AB，AO2为两邻边作平行四边形ABC2O2，…，依此类推，则平行四边形ABCnOn的面积为 ．
17．如图，等腰△ABC的面积是12，AB＝AC，BC＝4，EF垂直平分AB，点D为BC的中点，点M为线段EF上一点，则△BDM的周长的最小值为 ．
18．如图，正方形ABCD中，AB＝4，BE＝CE，F是边AB上一动点，连接EF，翻折△BEF至△GEF，使得B落在G处，连接DG，当四边形AFGD的周长取得最小值时，则BF＝ ．
19．如图，直线y＝kx+b分别与x轴、y轴交于C、D两点，与反比例函数y＝mx的图象交于A（1，3）、B（3，1）两点，过点A作AE⊥y轴于点E，过点B作BF⊥x轴于点F，连结EF.给出以下结论：①m＝3，k＝﹣1，b＝4；②EF∥AB；③五边形AEOFB的面积＝6；④四边形DEFB与四边形AEFC的周长相等.所有正确的结论有 .（填正确的序号）
20．如图，已知直线 y=−13x+1 与坐标轴交于A，B两点，矩形ABCD的对称中心为M，双曲线 y=kx （x＞0）正好经过C，M两点，则直线AC的解析式为： .
三、解答题
21．如图1，△ABC是等腰直角三角形，∠ACB=90°，AC=BC，先将边BC沿过点B的直线l对折得到BD，连接CD，然后以CD为边在左侧作△CDE，其中∠CDE=90°，CD=DE，BD与CE交于点F，连接BE，AD．
（1）求证：△ACD≌△BDE；
（2）如图2，当点D在△ABC的斜边AB上时，请直接写出用BC，BE表示AB的关系式；
（3）如图3，当点D在△ABC的内部时，若点F为BD的中点，且△ACD的面积为10，求△CDF的面积．
22．定义：在四边形中，若一条对角线能平分一个内角，则称这样的四边形为“可折四边形”．
例：如图1，在四边形ABCD中，∠ABD=∠DBC，则四边形ABCD是“可折四边形”．
利用上述知识解答下列问题．
（1）在平行四边形、矩形、菱形、正方形中，一定是“可折四边形”的有：__________．
（2）在四边形ABCD中，对角线BD平分∠ABC．
①如图1，若∠ABC=60°，BD=4，求AD+CD的最小值．
②如图2，连接对角线AC，若DC刚好平分∠ACE，且∠BDC=25°，求∠DAC的度数．
③如图3，若∠ABC=60°，AD=CD，对角线AC与BD相交于点E，当BC=6，且△AEB为等腰三角形时，求四边形ABCD的面积．
23．定义： 图象与 x 轴有两个交点的函数 y=−2x+4（x⩾m），2x+4（x（1） 如图 11-8， 已知直线 l：x=1， 关于直线 l提示 按时完成 “A 本”高效提分训练 1突碱的对称函数 y=−2x+4（x⩾1），2x+4（x<1） 与该直线交于点 C．
①直接写出点的坐标： A （ ▲ ， ▲ ） ， B（ ▲ ， ▲ ），C（ ▲ ， ▲ ）
②P 为关于直线 l 的对称函数图象上一点（点 P 不与点 C 重合）， 当 S△ABP= 32S△ABC 时， 求点 P 的坐标．
（2） 当直线 y=x 与关于直线 x=m 的对称函数有两个交点时， 求 m 的取值范围．
24．如图，在平面直角坐标系中，抛物线y=ax2+bx+3交y轴于点A，且过点B(−1，2)，C(3，0)．
（1）求抛物线的函数解析式；
（2）将抛物线向左平移m(m>0)个单位，当抛物线经过点B时，求m的值；
（3）若P是抛物线上位于第一象限内的一点，且S△ABC=2S△ACP，求点P的坐标．
答案解析部分
1．【答案】B
【解析】【解答】设三角形ABC底边BC上的高是h
h=ABsin∠ABC=8×sin60°=8×32=43
∵BC=2CF
∴CF=12BC=12×43=23
又DCFE是平行四边形
∴DE=CF=23
观察图中阴影，是以DE为共同底、两个高的和是h的两个三角形
∴S阴影=S△DEB+S△DEA=12×23×43=12
故选：B
【分析】阅读已知条件时，看到给了AB值和60°特殊角，就想到60度角所对直角边和邻边长可求；看到BC=2CF，且DCFE是平行四边形，就可以想到DE可求；观察图中阴影，发现是以DE为共同底、两个高的和是通过60°角的三角函数可求的两个三角形，至此边读题边思考，找到解决办法。
2．【答案】B
【解析】【解答】过点A作AM⊥OB于M，设点A坐标为（x，y)，
∵顶点A在双曲线y=4x（x＞0)图象上，
∴xy=4，
∴S△AMO=12OM•AM=12xy=2，
设B的坐标为（a，0)，
∵中点C在双曲线y=4x（x＞0)图象上，CD⊥OB于D，
∴点C坐标为（a+x2，y2)，
∴S△CDO=12OD•CD=12•a+x2•y2=2，
整理，ay+xy=16，
∵xy=4，
∴ay=16-4=12，
∵S△AOB=S△AOM+S△AMB
=2+12•（a-x)y
=2+12ay-12xy=2+12×12-12×4
=6，
又∵C为AB中点，
∴△AOC的面积为12×6=3．
故选B．
【分析】过点A作AM⊥OB于M，设点A坐标为（x，y)，根据过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S= 1 2 |k|．可求出S△AMO和S△AMB，进而求出S△AOB，又因为C为AB中点，所以△AOC的面积为△AOB面积的一半，问题得解．本题主要考查了反比例函数 y＝kx中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得三角形面积为12|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
3．【答案】D
【解析】【解答】解：连接BE，
∵点E是△ABC的内心，
∴AE平分∠BAC，故①符合题意；
∴∠BAD=∠DAC，
∴BD＝CD ，故②符合题意；
∴∠DBC=∠BAD，故③符合题意；
∵点E是△ABC的内心，
∴AE平分∠BAC，BE平分∠ABC，
∴∠BAD=∠CAD，∠ABE=∠CBE，
又∵∠CAD=∠CBD=∠BAD．
∴∠BED=∠ABE+∠BAD，∠DBE=∠CBE+∠CBD，
即∠BED=∠DBE，
故BD=DE．故④符合题意；
∵∠D=∠D，∠DBC=∠BAD，
∴△DFB∽△DBA，
∴DFBD＝BDDA ，
∴BD2=DF•DA．
∵BD=DE．
∴DE2=DF•DA，故⑤符合题意．
故答案为：D．
【分析】根据三角形的内心的性质、相似三角形的判定和性质及圆周角定理逐项判断即可。
4．【答案】D
【解析】【解答】解：①∵四边形ABCD是正方形，
∴AD=DC=BC，∠ADC=∠DCB=90°，
∵BF= CE，
∴BC-BF= DC-CE，即CF= DE，
∴△ADE≌△DCF (SAS)，
∴∠DAE=∠CDF，
∵∠CDF+∠ADG=90° ，
∴∠DAE+∠ADG=90°，
∴∠AGD=90°，
即AE⊥DM.
∵∠AGM= ∠AGD=90° ，
∵AE平分∠CAD，
∴∠MAG=∠DAG.
又∵AG=AG，
∴△AGM≌△AGD ( ASA )，
∴GM=GD，
∴AE垂直平分DM，故①正确，符合题意；
②连接BD与AC交于点O，连接PD，ND，如图：
∵AE垂直平分DM，P为AE上一点，
∴PD=PE.
∴PN+PM=PN+PD≥DN，
又∵点D为直线AC外一点，
∴DN⊥AC时，DN长度最小.
即点N与点O重合，且D，P，N三点共线时， PM+PN的值最小，
即PM+ PN= PN+PD≥DN≥DO，故PM+ PN的最小值为DO的长，
∵正方形ABCD的边长为4，
∴AC=BD=42，
∴DO=12BD=22，
即PM+ PN的最小值为22，故②错误，不符合题意；
③∵AE⊥DM，
∴∠DGE=90°，
∵∠ADE=90°，
∴∠DGE=∠ADE，
∵∠DEG=∠AED，
∴△DEG∽△AED，
∴DEAE=EGDE.
∴DE2=AE·EG，
由①知，CF=DE，
∴CF2=GE·AE，故③正确，符合题意；
④∵AE垂直平分DM，
∴AM=AD=4，
∵DO=12BD=22，
∴S△ADM=12×AM×DO=12×4×22=42，故④错误，不符合题意；
综述所述：正确的有①③
故答案为：D.
【分析】根据正方形的性质证得△ADE≌△DCF，再利用ASA证明△AGM≌△AGD，即可得出AE垂直平分DM，即可判断①；连接BD与AC交于点O，交AG于点H，连接PD，ND，当D，P，N三点共线时，PD+PN=DN，而当点N与点O重合时，DN⊥AC，DN最小，从而可得PM+PN的最小值，即可判断②；证明△DEG∽△AED，根据相似三角形的性质即可判断③；先求出AM的长，再根据三角形面积公式计算即可得出答案从而判断④.
5．【答案】C
【解析】【解答】解：根据题意知，将2021个形状、大小均相同的菱形按照如图所示的方式排成一列，得到2020个阴影菱形，且这些阴影菱形的大小完全一致，
如图，
由题意知，OA=OC，AB=BC=CD=AD=2，∠BAD=∠EOF，
由菱形的对角线平分一组对角可知∠EOC=∠DAO，
∴OE∥AD，
∴OE是△ACD的中位线
∴OE=12AD=1，
∴一个阴影菱形的周长为：1×4=4，
∴2020个阴影菱形的周长和为：4×2020=8080，
故答案为：C．
【分析】先通过菱形的性质和三角形中位线定理求出一个阴影菱形的边长，再计算2020个阴影菱形的周长总和即可.
6．【答案】C
【解析】【解答】解：∵平行四边形ABCD，
∴AB∥CD，AD=CB，AB=DC，BD=2OD，
∵E，F，G分别是OC，OD，AB的中点，
∴EF是△OBC的中位线，
∴EF=12CD=12AB，EF∥CD，
∵BD=2AD，
∴AD=OD=OB=BC，
∴BE⊥OC，
∴∠AEB=90°，
∵EG是△AEB的中线，
∴AG=EG=12AB=BG，
∴EF=EG，故②正确；
∴EF=BG，EF∥BG，
∴四边形BEFG是平行四边形，故③正确；
设FG与AC交于点M，
∵四边形BEFG是平行四边形，
∴FG∥BE，
∵BE⊥AC，
∴FG⊥AC，
∵EG=FE，
∴AC垂直平分FG，故④正确；
∴EG⊥AB不能证明
∴正确结论的序号为②③④.
故答案为：C.
【分析】利用平行四边形的性质可证得AB∥CD，AD=CB，AB=DC，BD=2OD，同时可证得EF是△OBC的中位线，利用三角形的中位线定理及BD=2AD，可证得AD=OD=OB=BC，EF∥CD，可推出EF=EG，可对②作出判断；利用有一组对边平行且相等的四边形是平行四边形，可证得四边形BEFG是平行四边形，可对③作出判断；设FG与AC交于点M，利用平行四边形的性质可证得FG∥BE，再由BE⊥AC，可推出FG⊥AC，利用等腰三角形的性质，可证得AC垂直平分FG，可对④作出判断；
7．【答案】B
【解析】【解答】解：延长EF，DA交于G，连接DE，如下图所示：
∵F是AB的中点，∴AF=BF，
∵四边形ABCD是平行四边形，
∴AB∥BC，∴∠GAB=∠EBF
且∠GFA=∠EFB，∴△AFG≌△BFE(ASA)，
设 BE=AG=x ，
由GF=EF，且∠DFE=90°知，
DF是线段GE的垂直平分线，
∴DE=DG=AG+AD=x+2 ，
在Rt△GAE中， AE2=AB2−BE2=(6)2−x2 ．
在Rt△AED中， AE2=DE2−AD2=(x+2)2−22 ，
∴(x+2)2−22=6−x2 ，解得 x=1 ，
∴AE=(6)2−12=5 ，
故答案为：B．
【分析】延长EF，DA交于G，连接DE，先证明△AFG≌△BFE，进而得到BE=AG，F是GE的中点，结合条件BF⊥GE进而得到BF是线段GE的垂直平分线，得到GD=DE，最后在Rt△AED中使用勾股定理即可求解.
8．【答案】A
【解析】【解答】解：如图，连接AC，BD， A1C1 ， B1D1 .
∵ 四边形ABCD是矩形，
∴AC=BD ， AD=BC ， AB=CD .
∵A1 ， B1 ， C1 ， D1 分别是矩形四个边的中点，
∴A1D1=B1C1=12BD，A1B1=C1D1=12AC ，
∴A1D1=B1C1=A1B1=C1D1 ，
∴四边形A1B1C1D1是菱形，
∵A1C1=AD=a ， B1D1=AB=b ，
∴四边形A1B1C1D1的面积为： 12A1C1⋅B1D1=12ab=12S▭ABCD .
同理，由中位线的性质可知，
D2C2=A2B2=12AD=12a ， D2C2//A2B2//AD ，
D2A2=C2B2=12AB=12b ， D2A2//C2B2//AB ，
∴四边形A2B2C2D2是平行四边形，
∵AD⊥AB ，
∴C2D2⊥D2A2 ，
∴四边形A2B2C2D2是矩形，
∴四边形A2B2C2D2的面积为： C2D2⋅A2D2=12a⋅12b=14S▭ABCD=12S菱形A1B1C1D1 .
∴每一次操作后得到的四边形面积为原四边形面积的一半，
∴四边形AnBnCnDn的面积是 ab2n .
故答案为：A.
【分析】连接AC，BD，A1C1 ， B1D1 ，易证四边形A1B1C1D1是菱形，可得四边形A1B1C1D1 的面积为矩形ABCD面积的一半，则四边形A1B1C1D1 的面积=12ab，易证四边形A2B2C2D2是矩形，可得矩形A2B2C2D2的面积==12a⋅12b=14S▭ABCD，从而得出每一次操作后得到的四边形面积为原四边形面积的一半，据此即可求解.
9．【答案】B
【解析】【解答】解：∵在正方形 ABCD 中， PE⊥BC 于点 E ， PF⊥CD 于点 F ，
∴∠PEC=∠PFC=∠BCD=90°，
∴四边形 PECF 是矩形，故①符合题意；
连接PC，
∵四边形 PECF 是矩形，
∴EF=PC，
∵AD=CD，∠ADP=∠CDP=45°，DP=DP，
∴△ADP≌△CDP ，
∴AP=CP=EF，故②符合题意；
随着点P的移动， PD=AD 不一定成立，故③不符合题意；
延长AP交EF于点H，延长FP交AB于点G，
∵BD平分∠ABC，PG⊥AB，PE⊥BC，
∴PG=PE，
∵AP＝PC，∠AGP＝∠EPF＝90°，
∴△AGP≌△FPE（HL），
∴∠BAP＝∠PFE，
∵∠AGP＝90°，
∴∠BAP＋∠APG＝90°，
∵∠APG＝∠HPF，
∴∠PFH＋∠HPF＝90°，
∴AP⊥EF，故④符合题意，
∴正确的说法是①②④，
故答案为：B．
【分析】由正方形的性质及垂直的定义，可得∠PEC=∠PFC=∠BCD=90°，可证四边形 PECF 是矩形，据此判断①；连接PC，证明△ADP≌△CDP ，可得AP=CP=EF，据此判断②；随着点P的移动， PD=AD 不一定成立，据此判断③；延长AP交EF于点H，延长FP交AB于点G，证明△AGP≌
△FPE（HL），可得∠BAP＝∠PFE，可求出∠PFH＋∠HPF＝90°，即得∠PHF=90°，据此判断④.
10．【答案】D
【解析】【解答】解：如图所示，延长EF交AC于点M，延长DF交AC于点N，
∵BD==13BA，BE=14BC，
∴BA=3BD，BC=4BE，
∵DF∥BC，即DN∥BC，
∴ADBD=ANAC=2，
∵EF∥AB，即EM∥AB，
∴CEBE=CMAM=3，
设AM=m，则：CM=3m，
∴AC=AM+CM=4m，
∴AN=23AC=83m，
∴MN=AN-AM=53m，
∵FM∥AD，
∴△FMN∽△DAN，
∴S△FMNS△DAN=MN2AN2=（53）2（83）2=2564，
设S△FMN=a，则S△DAN=64a，
∴S四边形ADFM=S△DAN-S△FMN=39a，
同理，可根据FN∥EC，可得：S△MEC=81a，S四边形FECN=46a，
∵DN∥BC，
∴S△ADNS△ABC=AN2AC2=（83）2（4）2=49，
∴S△ABC=144a，
∴S四边形BDFE=S△ABC-S四边形ADFM-S△MEC=144a-39a-81a=24a，
∴24a=2，
∴a=112，
∴S△ABC=144a=12.
故答案为：D。
【分析】延长EF交AC于点M，延长DF交AC于点N，设AM=m，首先根据平行线分线段成比例分别得出CM=3m，AN=83m，AC=3m，MN=53m，然后根据相似三角形的性质，从而求得三角形面积之间的关系，即可求出答案。
11．【答案】B
【解析】【解答】解：如图，过点 E 作 EF⊥AC 于 F ，作 BH⊥AC 于点 H ，
∴∠EFD=∠BHD=90∘ ，
∵BH2=BC2−CH2 ， BH2=AB2−AH2 ， AB=AC=5，BC=45 ，
∴80−(5+AH)2=25−AH2 ，
∴AH=3 ，
∴CH=8 ，
∵将线段 BD 绕 D 点顺时针旋转90°得到线段 ED ，
∴BD=DE ， ∠BDE=90∘ ，
∴∠BDF+∠EDF=90∘ ，且 ∠EDF+∠DEF=90∘ ，
∴∠DEF=∠BDF ，
在 ΔBDH 和 ΔDEF 中，
∠BDF=∠AEF∠BHD=∠EFDBD=DE ，
∴ΔBDH≅ΔDEF(AAS) ，
∴EF=DH ，
∵DH=CH−CD=8−CD ，
∴EF=8-CD
∵ΔCDE 面积 =12CD×EF=12×CD×(8−CD)=−12(CD−4)2+8 ，
∴当 CD=4 时， ΔCDE 面积的最大值为8，
故答案为：B.
【分析】过点 E 作 EF⊥AC 于 F ，作 BH⊥AC 于点 H ，由勾股定理可求 AH=3 ，由旋转的性质可求 BD=DE ， ∠BDE=90∘ ，由 AAS 可证 ΔBDH≅ΔDEF ，可得 EF=DH ，由三角形面积公式和二次函数的性质可求解.
12．【答案】A
【解析】【解答】解：由题意得分两种情况：
①如图1，∠D'AB'=90°，延长C'B'交AB于G，过点D'作D'H⊥AB，交BA的延长线于H，
∴∠H=∠AGB'=∠BGB'=90°，
∵四边形ABCD是矩形，
∴∠BAD=∠C=90°，AD=BC=3，
∵tan∠ABD=ADAB=B'GBG，即B'GBG=34，
设B'G=3x，BG=4x，
∴BB'=a=5x，
由平移得：DD'=BB'=5x，
∴D'H=3+3x，AH=BG=4x，
∴AG=AB−BG=4−4x，
∵∠D'AB'=∠HAD'+∠BAB'=90°，
∠AD'H+∠HAD'=90°，
∴∠AD'H=∠GAB'，
∵∠H=∠AGB'=90°，
∴△D'HA∽△AGB'，
∴D'HAG=AHB'G，即3+3x4−4x=4x3x，
∴x=725，
∴a=5×725=75；
②如图2，∠AB'D'=90°，延长C'B'交AB于M，则C'M⊥AB，
∴∠AMB'=90°，
由平移得：B'C'=BC=3，
同理设B'M=3m，BM=4m，则BB'=a=5m，
∴AM=4−4m，
∵∠AB'M+∠D'B'C'=90°，∠MAB'+∠AB'M=90°，
∴∠D'B'C'=∠MAB'，
∵∠C'=∠AMB'=90°，
∴△D'C'B'∽△B'MA，
∴C'D'MB'=B'C'AM，即43m=34−4m，
∴m=1625，
∴a=5m=5×1625=165；
综上，a的值是75或165．
故答案为：A
【分析】根据题意分类讨论：①∠D'AB'=90°，延长C'B'交AB于G，过点D'作D'H⊥AB，交BA的延长线于H，进而根据矩形的性质得到∠BAD=∠C=90°，AD=BC=3，再运用锐角三角函数的定义即可设B'G=3x，BG=4x，进而根据平移的性质得到DD'=BB'=5x，再结合题意运用相似三角形的判定与性质即可求解；②∠AB'D'=90°，延长C'B'交AB于M，则C'M⊥AB，根据平移的性质得到B'C'=BC=3，同理设B'M=3m，BM=4m，则BB'=a=5m，进而结合题意运用相似三角形的判定与性质即可求解。
13．【答案】2；102613
【解析】【解答】在矩形ABCD中，∠A=∠ABC=90°，AB=CD=10，AD=BC=12，
由折叠的性质可得AB=BE，∠BEF=90°，
∴四边形ABEF是矩形，∠CEF=180°-90°=90°，
∵AB=BE，
∴四边形ABEF是正方形，
∴AB=BE=EF=AF=10，
∴DF=BC-BE=2，
由勾股定理可得CF=CE2+EF2=22+102=226,
连接CF，如图，
由旋转的性质可得∠BEF=∠CNF=90°，EF=NF，
∵CF=CF，
∴Rt△ECF≅Rt△NCF(HL)，
∴CN=CE=2，EF=NF=10，
∴C、D在EN的垂直平分线上，
∴CF⊥EN，
∴四边形ECNE的面积为12EN·CF=2×12×10×2,
∴12×EN×226=2×12×10×2,
解得EN=102613，
【分析】先证明四边形ABEF是正方形，得到AB=BE=EF=AF=10，DF=BC-BE=2，连接CF，利用勾股定理求得CF的值以及旋转的性质，通过HL证明Rt△ECF≅Rt△NCF，从而得到CN=CE=2，EF=NF=10，证明C、D在EN的垂直平分线上，最后利用四边形ECNE的面积为12EN·CF=2×12×10×2,代入数据计算即可求解.
14．【答案】2或4或 92 或 94
【解析】【解答】解： ∵△ABC 是边长为3的等边三角形，
∴∠ABC=∠ACB=60°，AB=BC=AC=3 ，
由题意，分以下四种情况：
①如图，当点M在边 BC 上，点N在边 AC 上时，
在 △ABM 和 △BCN 中， ∠BAM=∠CBNAB=CB∠ABM=∠BCN ，
∴△ABM≅△BCN(ASA) ，
∴BM=CN=1 ，
∴AN=AC−CN=3−1=2 ；
②当点M在边 BC 上，点N在边 AC 延长线上时，
如图，过点N作 ND//AB ，交 BC 延长线于点D，
∴∠D=∠ABM=60° ，
∵∠DCN=∠ACB=60° ，
∴△CDN 是等边三角形，
∴CN=DN=CD ，
在 △ABM 和 △BDN 中， ∠BAM=∠DBN∠ABM=∠D ，
∴△ABM∼△BDN ，
∴DNBM=BDAB=BC+CDAB=BC+DNAB ，即 DN1=3+DN3 ，
解得 DN=32 ，
∴CN=32 ，
∴AN=AC+CN=3+32=92 ；
③当点M在边 CB 延长线上，点N在边 AC 上时，
如图，过点N作 ND//AB ，交 BC 于点D，
∴∠CDN=∠ABC=60°=∠ACB ，
∴△CDN 是等边三角形，
∴CN=DN=CD ，
∵∠CDN=∠ABC=60° ，
∴∠BDN=∠ABM=120° ，
在 △BDN 和 △ABM 中， ∠DBN=∠BAM∠BDN=∠ABM ，
∴△BDN∼△ABM ，
∴DNBM=BDAB=BC−CDAB=BC−DNAB ，即 DN1=3−DN3 ，
解得 DN=34 ，
∴CN=34 ，
∴AN=AC−CN=3−34=94 ；
④如图，当点M在边 CB 延长线上，点N在边 AC 延长线上时，
∵∠ABC=∠ACB=60° ，
∴∠ABM=∠BCN=120° ，
在 △ABM 和 △BCN 中， ∠BAM=∠CBNAB=CB∠ABM=∠BCN ，
∴△ABM≅△BCN(ASA) ，
∴BM=CN=1 ，
∴AN=AC+CN=3+1=4 ；
综上， AN 的值为2或4或 92 或 94 ，
故答案为：2或4或 92 或 94 ．
【分析】分四种情况分别画出图形，两条全等三角形或相似三角形的性质解决问题即可。
15．【答案】2
【解析】【解答】解：∵BC⋅OA=6，
∴S△OBC= 12BC⋅OA= 12 ×6=3，
过D点作DE⊥x轴，垂足为E，
由双曲线上点的性质，得S△AOC=S△DOE= 12k，
∵DE⊥x轴，AB⊥x轴，
∴DE∥AB，
∴△OAB∽△OED，
又∵OB=2OD，
∴S△OAB=4S△DOE=2k，
由S△OAB−S△OAC=S△OBC，
得2k− 12k=3，
解得：k=2.
故答案为：2.
【分析】先根据题意求出△OBC的面积，过D点作DE⊥x轴，垂足为E，由双曲线上点的性质可知S△AOC=S△DOE= 12k，又可证△OAB∽△OED，根据相似三角形面积比等于相似比的平方，表示△OAB的面积，利用S△OAB-S△OAC=S△OBC，列方程求k．
16．【答案】52n
【解析】【解答】解：后面的每一个平行四边形都与第一个矩形ABCD同底不同高，而第n个平行四边形的高是矩形ABCD的12n ，所以平行四边形ABCnOn的面积为 52n．
【分析】根据矩形和平行四边形面积公式及中位线定理，发现依次的平行四边形都是与矩形等底、高依次为前一个图形高的一半的关系，故得到第n个平行四边形的高是矩形ABCD的 12n，可得第n个平行四边形的高是矩形ABCD的 52n。
17．【答案】8
【解析】【解答】解：连接AM，AD，如图
.
∵ △ABC是等腰三角形，点D为BC的中点，
∴ AD为BC边上的高，
∵ EF垂直平分AB，
∴ AM=BM，
∴ C△BDM =AM+BD+DM=12 BC+AM+DM=2+AM+DM.
∴ C△BDM min=2+(AM+DM)min.
∵ 两点之间线段最短，
∴AM+DM的最小值为AD，
∴ C△BDM min=2+AD.
∵ 等腰△ABC的面积是12，BC=4，
∴ AD=6，
∴ C△BDM min=8.
故答案为：8.
【分析】根据等腰三角形的三线合一得AD是BC边上的高线，再由垂直平分线的性质得AM=BM，再根据两点之间线段最短即可求得.
18．【答案】5+1
【解析】【解答】解：如图，连接ED，FG，DF，
∵正方形ABCD，AB=4，
∴∠ABC=∠DCB=90°，DC=AD=BC=4，
∵翻折△BEF至△GEF，BE=EC，
∴BE=EG=EC=2，
∴G点在以E为圆心，半径为2的圆上运动，
∴当E、G、D三点共线时，GD的长最短，此时FG=BF的长最大，
∴AF的长最短，
∴四边形AFGD的周长最小，
在Rt△DCE中，ED=22+42=25，
∴GD=25-2，
设FG=BF=x，AF=4-x，
在Rt△FAD和Rt△FGD中，DF2=AF2+AD2=FG2+GD2，
∴（4-x）2+16=x2+（25-2）2，
整理，解得x=5+1，
∴BF=5+1.
故答案为：5+1.
【分析】如图，连接ED，FG，DF，由正方形性质得∠ABC=∠DCB=90°，DC=AD=BC=4，由翻折性质得BE=EG=EC=2，可推出G点在以E为圆心，半径为2的圆上运动，当E、G、D三点共线时，GD的长最短，此时FG=BF的长最大，AF的长最短，即四边形AFGD的周长最小，在Rt△DCE中，由勾股定理求得ED25，从而得GD=25-2，设设FG=BF=x，AF=4-x，在Rt△FAD和Rt△FGD中，由勾股定理得DF2=AF2+AD2=FG2+GD2，即（4-x）2+16=x2+（25-2）2，整理，解得x=5+1，即可求出
四边形AFGD的周长最小时，BF的长.
19．【答案】①②④
【解析】【解答】解：∵直线y＝kx+b过A（1，3）、B（3，1）两点，
∴k+b=33k+b=1，
解得k=−1b=4，
∴直线的函数关系式为y＝﹣x+4，
又∵反比例函数y＝mx的图象过A（1，3），
∴m＝1×3＝3，
∴反比例函数的关系式为y＝3x，
因此①正确；
∵AE⊥y轴，BF⊥x轴，
∴E（0，3），F（3，0），
∴OE＝OF＝3，
又∵直线y＝﹣x+4与x轴的交点C（4，0），与y轴的交点D（0，4），
∴OC＝OD＝4，
∴AE＝DE＝BF＝FC＝1，
∴∠BCF＝∠EFO＝45°，
∴EF∥AB，
因此②正确；
S五边形AEOFB＝S△COD﹣S△ADE﹣S△BCF
＝12×4×4﹣12×1×1﹣12×1×1
＝7，
因此③不正确；
在直角△ADE中，AD＝DE2+AD2=12+12=2，
在直角△BCF中，BC=BF2+FC2=12+12=2 ，
在直角△EOF中，EF＝OE2+OF2=32+32=32，
在直角△COD中，CD ＝OC2+OD2=42+42=42，
∴BD=CD-BC=42−2=32，AC=CD-AD=42−2=32，
∴四边形DEFB的周长为DE+EF+BF+BD＝1+32+1+32＝2+62，
四边形AEFC的周长为AE+EF+FC+AC＝1+32+1+32＝2+62，
∴四边形DEFB与四边形AEFC的周长相等，
因此④正确；
综上所述，正确的结论有：①②④，
故答案为：①②④.
【分析】根据待定系数法求出函数关系式可确定k、b、 m的值，并对①作出判断；确定点E、F的坐标及直线AB与x轴、y轴交点C、D的坐标，利用等腰直角三角形的性质可对②作出判断；根据S五边形AEOFB＝S△COD﹣S△ADE﹣S△BCF列式计算即可对③作出判断；由坐标求出相应的线段的长，根据勾股定理求出AD、BC、EF. CD的长，再求出BD、AC的长，分别计算出四边形DEFB与四边形AEFC的周长，即可对④作出判断.
20．【答案】y=﹣2x+6
【解析】【解答】解：在y=﹣ 13 x+1中，令x=0，得y=1，令y=0，x=3，∴A（3，0），B（0，1），∴OA=3，OB=1，
过C作CE⊥y轴于E.
∵四边形ABCD是矩形，
∴∠CBA=90°，
∴∠CBE+∠OBA=∠OBA+∠BAO=90°，
∴∠CBE=∠BAO.∵∠BEC=∠AOB=90°，
∴△BCE∽△ABO，
∴OBOA=CEBE = 13 ，设CE=x，则BE=3x，
∴C（x，3x+1）.
∵矩形ABCD对称中心为M，
∴M（ x+32，3x+12 ）.
∵双曲线y= kx （x＞0）正好经过C，M两点，
∴x（3x+1）= x+32⋅3x+12 ，解得：x1=1，x2=﹣ 13 （舍）
∴C（1，4），设直线AC的解析式为：y=kx+b，把A（3，0）和C（1，4）代入得： 3k+b=0k+b=4 ，解得： k=−2b=6 ，
∴直线AC的解析式为：y=﹣2x+6.故答案为y=﹣2x+6.
【分析】先求出点AB的坐标，即得OA=3，OB=1，过C作CE⊥y轴于E，利用两角分别相等可证△BCE∽△ABO，可得OBOA=CEBE = 13，设CE=x，则BE=3x，可得C（x，3x+1），利用中点坐标公式可得M（ x+32，3x+12 ），根据反比例函数点的坐标特征可得x（3x+1）= x+32⋅3x+12，求出x的值，可得C（1，4），利用待定系数法求出直线AC的解析式即可.
21．【答案】（1）证明：∵边BC沿过点B的直线l对折得到BD，
∴BC=BD，
∴∠BCD=∠BDC，
∵∠ACB=∠CDE=90°，
∴∠ACB−∠BCD=∠CDE−∠BDC，
∴∠ACD=∠BDE，
∵AC=BC，
∴BD=AC，
∵CD=DE，
∴△ACD≌△BDE(SAS)；
（2）解：AB=BC+BE
（3）解：如图，
设直线l交CD于点H，交CE于K，取DH的中点G，连接FG，
∵点F是BD的中点，
∴FG∥BH，
∴CKFK=CHGH，
由折叠得：CH=DH，
∴CH=2GH，
∴CKFK=2，
∵l⊥CD，CD⊥DE，
∴FG∥DE，
∴FKEF=GHDG=1，
∴CFEF=3，
∴S△CDF：S△DEF=3：1，
由（1）知：△BDE≌△ACD，
∴S△BDE=S△ACD=10，
∵点F是BD的中点，
∴S△DEF=12S△ACD=5，
∴S△CDF=15．
【解析】【解答】解：（2）由（1）知：△ACD≌△BDE，
∴AD=BE，
∴AB=BD+AD=BD+BE，
∵BC=BD，
∴AB=BC+BE；
【分析】（1）由对折及已知可得BC=BD=AC，∠BCD=∠BDC，由∠ACB=∠CDE=90°可推出∠ACD=∠BDE，根据SAS可证△ACD≌△BDE；
（2）由（1）知△ACD≌△BDE，可得AD=BE，由AB=BD+AD=BD+BE即可求解；
（3）设直线l交CD于点H，交CE于K，取DH的中点G，连接FG，可得FG∥BH，利用平行线分线段成比例可得CKFK=CHGH，由折叠知CH=DH，可得CH=2GH，即得CK=2FK，易得FG∥DE，可得FKEF=GHDG=1，从而得出CFEF=3，继而得出S△CDF：S△DEF=3：1，进一步即可求解.
22．【答案】（1）菱形、正方形；
（2）①AD+CD的最小值是4；②∠DAC=65°；③93或273．
23．【答案】（1）解：①-2 0 2 0 1 2点 P 的坐标为 −72，−3 或 −12，3 或 72，−3．
（2）解：−224．【答案】（1）解：把点B(−1，2)，C(3，0)代入抛物线，得
a-b+3=29a+3b+3=0
解得：a=−12，b=12
∴y=−12x2+12x+3
（2）解：∵y=−12x2+12x+3=−12(x−12)2+258
∴当抛物线向左平移m个单位时，y=−12(x−12+m)2+258
把B(−1，2)代入得：−12(−1−12+m)2+258=2，
解得：m1=0（舍），m2=3
∴m=3．
（3）解：如图：
过点P作PE⊥x轴，交AC于点E
∵A（0，3），B（-1，2），C(3，0)，
∵AB=2，AC=32，BC=25
∵AB2+AC2=BC2，
∴∠BAC=90°，
∴S△ABC=12×2×32=3
∵A（0，3），C(3，0)，
∴直线AC解析式：y=−x+3
设P(t，−12t2+12t+3)，则E(t，−t+3)
∴PE=−12t2+32t，
∴S△ACP=12×3×(−12t2+32t)=−34t2+94t
∵S△ABC=2S△ACP，
∴2(−34t2+94t)=3，
解得：t1=1，t2=2
∴P1(1，3)，P2(2，2)
【解析】【分析】（1）利用待定系数法计算计算即可；
（2）先将一般式化成顶点式，根据“左加右减”的法则写出平移后的函数表达式，再把点B坐标带入，即可得到m的值，注意m>0；
（3）根据A，B，C三点坐标求出AB，AC，BC的长，利用勾股定理，发现△ABC是直角三角形，可求△ABC的面积；过P作PE⊥x轴交AC于点E，设出点P的坐标P(t，−12t2+12t+3)，利用直线AC的解析式表示出点E的坐标，得到PE，则△PAC的面积为S△PAC=12×PE×xc-xa，根据 S△ABC=2S△ACP，可求得t的值，从而得到点P的坐标.