2024年中考数学压轴题精选专项突破-折叠问题

这是一份2024年中考数学压轴题精选专项突破-折叠问题，共37页。试卷主要包含了选择题，填空题，解答题，实践探究题等内容，欢迎下载使用。

一、选择题（每题3分，共36分）
1．如图，矩形 ABCD 中， AB=6，BC=9 ，以 D 为圆心，3为半径作 ⊙D ， E 为 ⊙D 上一动点，连接 AE ，以 AE 为直角边作 Rt△AEF ，使 ∠EAF=90° ， tan∠AEF=13 ，则点 F 与点 C 的最小距离为（ ）
A．310−1B．37C．37−1D．910109
2．如图．在直角坐标系中，矩形ABC0的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点D的坐标为（ ）
A．(-45，125)B．(-25，135)C．(-12，135)D．(-35，125)
3．如图，在△ABC中，∠ACB＝90°，∠A＝30°，BC＝2，点D是AC边的中点，点E是AB边上一点，将△ADE沿直线DE折叠，得到△FDE，连接FC，EC.若四边形DECF是菱形，则BE的长为（ ）
A．1B．3C．2D．4﹣ 3
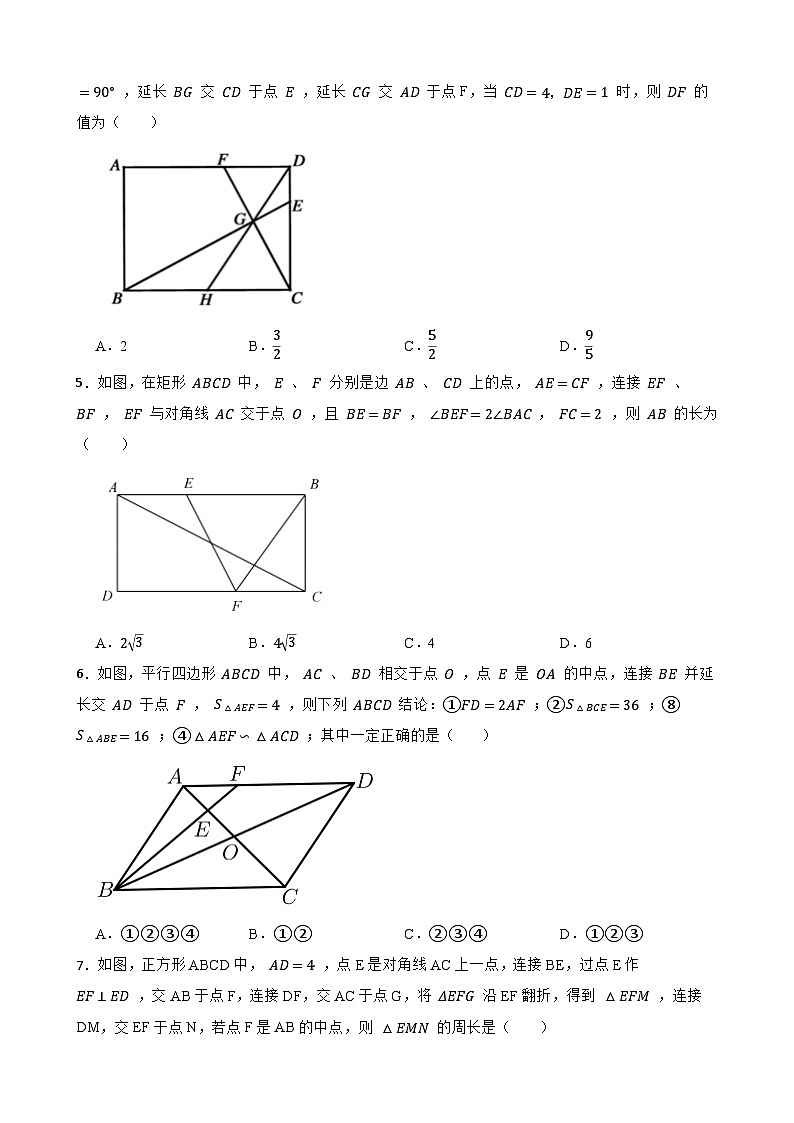
4．如图，在矩形 ABCD 中，点 H 为边 BC 的中点，点G为线段 DH .上的一点，且 ∠BGC=90° ，延长 BG 交 CD 于点 E ，延长 CG 交 AD 于点F，当 CD=4，DE=1 时，则 DF 的值为（ ）
A．2B．32C．52D．95
5．如图，在矩形 ABCD 中， E 、 F 分别是边 AB 、 CD 上的点， AE=CF ，连接 EF 、 BF ， EF 与对角线 AC 交于点 O ，且 BE=BF ， ∠BEF=2∠BAC ， FC=2 ，则 AB 的长为（ ）
A．23B．43C．4D．6
6．如图，平行四边形 ABCD 中， AC 、 BD 相交于点 O ，点 E 是 OA 的中点，连接 BE 并延长交 AD 于点 F ， S△AEF=4 ，则下列 ABCD 结论：①FD=2AF ；②S△BCE=36 ；⑧S△ABE=16 ；④△AEF∽△ACD ；其中一定正确的是（ ）
A．①②③④B．①②C．②③④D．①②③
7．如图，正方形ABCD中， AD=4 ，点E是对角线AC上一点，连接BE，过点E作 EF⊥ED ，交AB于点F，连接DF，交AC于点G，将 ΔEFG 沿EF翻折，得到 △EFM ，连接DM，交EF于点N，若点F是AB的中点，则 △EMN 的周长是（ ）
A．32+102B．42+102C．52+102D．62+102
8．已知，O是矩形ABCD对角线的交点，作DE//AC，AE//BD，AE，DE相交于点E，连结BE.下列说法正确的是（ ）
①四边形DEAO为菱形；②AE=AB；③∠BAE=120°；④若∠BED=90°，则AD=BE.
A．①③B．①②④C．①④D．③④
9．如图，在△ABC中，D是AC边上的中点，连结BD，把△BDC′沿BD翻折，得到△ BDC' ，DC与AB交于点E，连结 AC' ，若AD=AC′=2，BD=3则点D到BC的距离为（ ）
A．332B．3217C．7D．13
10．如图1，以Rt△ABC的各边为边向外作等边三角形，编号分别为①，②，③．如图2，将①，②叠放在③中，若四边形EGHF与GDCH的面积之比是16164，则sin∠ABC的值是（ ）
A．817B．815C．513D．35
11．已如正方形EFGH的边EF在△ABC的边BC上，点G、H分别在AB和AC上，BC=6，S正方形EFGH=4，则AB+AC的最小值为（ ）
A．62B．37C．35D．10
12．在 Rt△ABC 中， ∠ACB=90°，∠CAB=36° ，在直线 AC 或 BC 上取点 M ，使得 △MAB 为等腰三角形，符合条件的 M 点有（ ）
A．6个B．7个C．8个D．9个
二、填空题（每题3分，共18分）
13．如图，在矩形ABCD中，E为CD上一点，若△ADE沿直线AE翻折，使点D落在BC边上点 D' 处，F为AD上一点，且 DF=CD' ，EF与BD相交于点G， AD' 与BD相交于点H， D'E//BD ，HG=2，则BD= .
14．如图，在矩形ABCD内放入四个小正方形和两个小长方形后形成中心对称图形，其中小正方形的顶点E，F 分别在边AD，BC上，小长方形的长与宽的比值均为 4，则ADAB的值为 .
15．如图，已知直线 y=43x−3 与 x 轴、 y 轴分别交于A，B两点，P是以 C(0，1) 为圆心，1为半径的圆上一动点，连接 PA ， PB ，当 ΔPAB 的面积最大时，点P的坐标为 ．
16． 图1是一张足够长的纸条，其中PN∥QM，点A、B分别在PN、QM上，记∠ABM=α(0°<α<90°)．如图2，将纸条折叠，使BM与BA重合，得折痕BR1，如图3，将纸条展开后再折叠，使BM与BR1重合，得折痕BR2，将纸条展开后继续折叠，使BM与BR2重合，得折痕BR3…依此类推，第n次折叠后，∠ARnN= （用含a和n的代数式表示）
17．如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点F在边AC上，并且CF＝1，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是 .
18．如图，正方形纸片 ABCD 的边长为4，点 F 在边 AD 上，连接 BF ，将纸片沿着直线 BF 翻折，点 A 的对应点为点 G ，连接 AG 并延长交 CD 于点 E ，若 DE=3 ，则 GE= .
三、解答题（共2题，共13分）
19．如图所示，在Rt△BCD中，CD＝CB，∠BCD＝90°，E为△BCD内一点，且DE＝DC，BE＝CE．求∠CDE的度数．
20．问题提出：如图①，将一张直角三角形纸片△ABC折叠，使点A与点C重合，这时DE为折痕，△CBE为等腰三角形；再继续将纸片沿△CBE的对称轴EF折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”.
知识运用：
（1）如图②，正方形网格中的△ABC能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕；
（2）如图③，在正方形网格中，以给定的BC为一边，画出一个斜三角形ABC，使其顶点A在格点上，且△ABC折成的“叠加矩形”为正方形；
（3）若一个锐角三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是什么？结合图③，说明理由。
拓展应用：
（4）如果一个四边形一定能折成"叠加矩形"，那么它必须满足的条件是什么？
四、实践探究题（共4题，共33分）
21．探究问题：
（1）方法感悟：
如图①，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF，求证DE+BF=EF．
感悟解题方法，并完成下列填空：
将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，由旋转可得：
AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，
∴∠ABG+∠ABF=90°+90°=180°，
因此，点G，B，F在同一条直线上．
∵∠EAF=45°
∴∠2+∠3=∠BAD−∠EMF=90°−45°−45°．
∵∠1=∠2，
∴∠1+∠3=45°．
即∠GAF=∠ ▲ ．
又AG=AE，AF=AF
∴△GAF≌ ▲ ．
∴ ▲ =EF，故DE+BF=EF．
（2）方法迁移
如图②，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=∠12DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．
（3）问题拓展：
如图③，在四边形ABCD中，AB=AD，E，F分别为DC，BC上的点，满足∠EAF=∠12DAB，试猜想当∠B与∠D满足什么关系时，可使得DE+BF=EF，请直接写出你的猜想（不必说明理由）．
22．如图
（1）尝试解决：如图1，在△EDF中，∠EDF=90°，DE=DF，点M在边EF上运动（M不与点E，F重合），连接DM，过点D作线段DN⊥DM，垂足为点D，且DN=DM，连接NF，求出∠EFN的度数；
（2）类比探究：如图2，在△EDF中，∠EDF=90°，DE=DF，点M在边EF上运动（M不与点E，F重合），连接DM，以DM为腰在DE上方作等腰Rt△MDN，其中∠MDN=90°，DM=DN，试问线段DM，EM，FM之间有怎样的等量关系？写出结论并证明；
（3）拓展应用：如图3，在△EDF中，∠EDF=90°，DE=DF，在DF左侧作∠DMF=45°，若DM=5，FM=2，求出EM的长度．
23．
（1）【感知】如图①，在四边形ABCD中，∠C＝∠D＝90°，点E在边CD上，∠AEB＝90°，求证：AEEB=DECB。
（2）【探究】如图②，在四边形ABCD中，∠C＝∠ADC＝90°，点E在边CD上，点F在边AD的延长线上，∠FEG＝∠AEB＝90°，且EFEG=AEEB，连接BG交CD于点H。求证：BH＝GH。
（3）【拓展】如图③，点E在四边形ABCD内，∠AEB+∠DEC＝180°，且AEEB=DEEC，过E作EF交AD于点F，若∠EFA＝∠AEB，延长FE交BC于点G。求证：BG＝CG。
24．【阅读材料】证明两条线段相等，常用的方法是应用全等三角形或等腰三角形的性质.如果两条线段不在同一个三角形中，且所在三角形明显不全等，此时就需要添加辅助线来构造全等三角形.
（1）【理解应用】如图(1)所示，在等腰三角形ABC中，AB=AC，D为BC上一点，且CD>BD，连接AD，小明对△ABC进行了如下操作：在CD上取一点E，使得AE=AD，连接AE，则可证明△ABD≌△ACE，请你补充小明操作过程的证明；
（2）【类比探究】如图(2)所示，在四边形ABCD中，AC平分∠BAD，∠ABC+∠ADC=180°，求证：CD=CB；
（3）【拓展应用】如图(3)所示，已知△ABC是边长为5 cm的等边三角形，点E在CA的延长线上，且AE=1.5 cm，连接EB，在线段BC上取点F，连接EF，使得EB=EF，请直接写出BF的长.
答案解析部分
1．【答案】A
【解析】【解答】解：如图，取 AB 的中点 G ，连接 FG ， FC ， GC ，DE．
∵∠EAF=90° ， tan∠AEF=13 ，
∴AFAE=13 ，
∵AB=6 ， AG=GB ，
∴AG=GB=3 ，
∵AD=9 ，
∴AGAD=39=13 ，
∴AFAE=AGAD ，
∵四边形 ABCD 是矩形，
∴∠BAD=∠B=∠EAF=90° ，
∴∠FAG=∠EAD ，
∴△FAG∼△EAD ，
∴FG：DE=AF：AE=1：3 ，
∵DE=3 ，
∴FG=1 ，
∴点 F 的运动轨迹是以 G 为圆心1为半径的圆，
∵GC=BC2+BG2=310 ，
∴FC≥GC−FG ，
∴FC≥310−1 ，
∴CF 的最小值为 310−1 ．
故答案为：A．
【分析】取AB证得△FAG∽△EAD，得到FG∶DE=AF∶AE=1∶3，即FG=1 ，点F的运动轨迹是以G为圆心1为半径的圆，当点F、G、C三点共线时，CF最小，在Rt△GBC中，BC=9，BG=3，勾股定理得出GC的长，进而由CF=GC-FG，即可得到结果.
2．【答案】A
【解析】【分析】如图，过D作DF⊥AF于F，根据折叠可以证明△CDE≌△AOE，然后利用全等三角形的 性质得到OE=DE，OA=CD=1，设OE=x，那么CE=3-x，DE=x，利用勾股定理即可求出OE的长度，而利用已知条件可以证明 △AEO∽△ADF，而AD=AB=3，接着利用相似三角形的性质即可求出DF、AF的长度，也就求出了D的坐标．
【解答】如图，过D作DF⊥AF于F，
∵点B的坐标为（1，3)，
∴AO=1，AB=3，
根据折叠可知：CD=OA，
而∠D=∠AOE=90°，∠DEC=∠AEO，
∴△CDE≌△AOE，
∴OE=DE，OA=CD=1，
设OE=x，那么CE=3-x，DE=x，
∴在Rt△DCE中，CE2=DE2+CD2，
∴（3-x)2=x2+12，
∴x=43，
又DF⊥AF，
∴DF∥EO，
∴△AEO∽△ADF，
而AD=AB=3，
∴AE=CE=3-43=53，
∴AEAD=EODF=AOAF
即533＝43DF＝1AF，
∴DF=125，AF=95，
∴OF=95-1=45，
∴D的坐标为(-45，125)
故选A．
【点评】此题主要考查了图形的折叠问题，也考查了坐标与图形的性质，解题的关键是把握折叠的隐含条件，利用隐含条件得到全等三角形和相似三角形，然后利用它们的性质即可解决问题
3．【答案】A
【解析】【解答】解：在△ABC中，
∵∠ACB＝90°，∠A＝30°，BC＝2，
∴∠B＝60°，AB＝2BC＝4，AC＝ 3 BC＝2 3 ，
∵点D是AC边的中点，
∴AD＝CD＝ 3 ，
由翻折变换可知，AD＝FD＝ 3 ，∠A＝∠DFE＝30°，
又∵四边形DECF是菱形，
∴DE＝DF＝CE＝CF＝CD＝ 3 ，
∴△DCF和△DCE都是正三角形，
∴∠DCE＝60°，
∴∠BCE＝90°﹣60°＝30°，
∴∠BEC＝180°﹣60°﹣30°＝90°，
在Rt△BCE中，∠B＝60°，BC＝2，
∴BE＝ 12 BC＝1.
故答案为：A.
【分析】由已知条件可得∠B＝60°，AB＝4，AC＝23，根据线段中点的概念可得AD＝CD＝3，由折叠的性质可得AD＝FD＝3，∠A＝∠DFE＝30°，由菱形的性质可得DE＝DF＝CE＝CF＝CD= 3，推出 △DCF、△DCE都是正三角形，进而求出∠DCE、∠BCE、∠BEC的度数，然后根据含30°角的直角三角形的性质进行求解.
4．【答案】A
【解析】【解答】解：连接FE
∵∠FGE=∠CGB=90° ，由四边形ABCD是矩形知：
∠FDE=∠BCD=90°
∴F、D、E、G四点共圆，故 ∠DFE=∠DGE
∵∠BGC=90° ，点H为边BC的中点，故
GH=12BC=BH=CH
∴∠HBG=∠HGB=∠EGD
∵∠BCD=∠BGC=90° 即得 ∠HBG+∠HCG=90°， ∠FCD+∠HCG=90°
∴∠HBG=∠FCD
∴∠DFE=∠FCD
△FDE∽△CDF
∴FDCD=DEDF，
DF2=CD×DE
∵CD=4， DE=1，
∴DF=CD×DE=4×1=2
故答案是A.
【分析】根据矩形的性质，可知 ∠FDE=∠BCD=90° ，得出F、D、E、G四点共圆，根据中点得出线段相等，得出角相等，再根据同角的余角相等，从而判断出 ∠HBG=∠FCD ∠DFE=∠FCD ，得出， △FDE∽△CDF 列出比例式解决即可.
5．【答案】D
【解析】【解答】解：如图，连接BO，
∵四边形ABCD是矩形，
∴DC∥AB，∠DCB=90°
∴∠FCO=∠EAO，
在△AOE和△COF中，
∠AOE=FOC∠FCO=∠EAOAE=CF ，
∴△AOE≌△COF，
∴OE=OF，OA=OC，
∵BF=BE，
∴BO⊥EF，∠BOF=90°，
∵∠FEB=2∠CAB=∠CAB+∠AOE，
∴∠EAO=∠EOA，
∴EA=EO=OF=FC=2，
在Rt△BFO和Rt△BFC中，
BF=BFFO=FC ，
∴Rt△BFO≌Rt△BFC，
∴BO=BC，
在Rt△ABC中，∵AO=OC，
∴BO=AO=OC=BC，
∴△BOC是等边三角形，
∴∠BCO=60°，∠BAC=30°，
∴∠FEB=2∠CAB=60°，
∵BE=BF，
∴△BEF是等边三角形，
∴EB=EF=4，
∴AB=AE+EB=2+4=6.
故答案为：D.
【分析】连接BO，根据矩形的性质可得DC∥AB，∠DCB=90°，根据平行线的性质可得∠FCO=∠EAO，证明△AOE≌△COF，得到OE=OF，OA=OC，推出∠EAO=∠EOA，则EA=EO=OF=FC=2，证明Rt△BFO≌Rt△BFC，得到BO=BC，易得△BOC是等边三角形，得到∠BCO=60°，∠BAC=30°，则∠FEB=2∠CAB=60°，进而推出△BEF是等边三角形，则EB=EF=4，然后根据AB=AE+EB进行计算.
6．【答案】B
【解析】【解答】解：①∵四边形 ABCD 是平行四边形，
∴OA=OC ， AD//BC ， AD=BC ，
∵点 E 是 OA 的中点，
∴CE=3AE ，
∵AF//BC ，
∴△AEF∽△CEB ，
∴BCFA=CEAE=3 ，
∴BC=3AF ，
∴AD=3AF
∴FD=2AF ，所以结论①符合题意；②∵△AEF∽△CEB ， CE=3AE ，
∴S△BCES△FAE=32 ，
∴S△BCE=9S△FAE=36 ，所以结论②符合题意；③∵△ ABE 和 △CBE 等高，且 BE=3AE ，
∴S△BCE=3S△ABE ，
∴S△ABE=12 ，所以结论③不符合题意；④假设 △AEF∽△ACD ，
∴EF//CD ，即 BF//CD ，
∵AB//CD ，
∴BF 和 AB 共线，
但点 E 是 OA 的中点，则 BE 与 AB 不共线，
∴假设不成立，即 △AEF 和△ ACD 不相似，所以结论④不符合题意．
综上所述：正确的结论有①②．
故答案为：B．
【分析】根据平行四边形的性质可得 AF//BC ，进而可得 △AEF∽△CEB ，然后根据相似三角形的性质、已知条件和平行四边形的性质即可得出AD=3AF ，进而可判断①；根据相似三角形的面积之比等于相似比的平方即可判断②；由△ ABE 和 △CBE 等高即可求出 △CBE 的面积，于是可判断结论③；假设 △AEF∽△ACD ，利用反证法即可得出矛盾，于是可判断④，进而可得答案．
7．【答案】C
【解析】【解答】解：如图1：过E作PQ⊥DC，交DC于P，交AB于Q，连接BE.
∵DC∥AB
∴PQ⊥AB，
∵四边形ABCD是正方形
∴∠ACD=45°
∴△PEC是等腰直角三角形
∴PE=PC.
设PC=x，则PE=x，PD=4-x，EQ=4-x.
∴PD=EQ，
∴∠DPE=∠EQF=90°，∠PED=∠EFQ.
∴△DPE≌△EQF
∴DE=EF
∵DE⊥EF
∴△DEF是等腰直角三角形
易证△DEC≌△BEC
∴DE=BE
∴EF=BE
∵EQ⊥FB
∴FQ=BQ= 12 BF
∵AB=4，F是AB的中点
∴BF=2
∴FQ=BQ=PE=1
∴CE= 2 ，PD=4-1=3
Rt△DAF中， DF=42+22=25
∴DE=EF= 10
如图2，
∵DC//AB.
∴△DGC∽△FGA
∴CGAG=DCAF=DGFG=42=2
∴AG=2AG，DG=2FG
∴FG=13×25=253
∵AC=42+42=42
∴CG=23×42=823
∴EG=823−2=523
连接GM、GN，交EF于H.
∵∠GFE=45°
∴△GHF是等腰直角三角形
∴GH=FH=2532=103
由折叠得：GM⊥EF，MH=GH= 103
∴∠EHM=∠DEF=90°
∴DE∥HM
∴△DEN∽△MNH
∴DEMH=ENNH
∴10103=ENNH=3
∴EN=3NH
∵EN+NH=EH= 2103
∴EN= 103
∴NH=EH-EN= 2103−102=106
在Rt△GNH中， GN=GH2+NH2=(103)2+(106)2=526
由折叠得：MN=GN，EM=EG
∴△EMN的周长为 EN+MN+EM=102+526+523=52+102 .
故答案为：C.
【分析】如图：过E作PQ⊥DC，交DC于P，交AB于Q，连接BE.先通过等腰三角形和全等三角形的判定和性质得到FQ=BQ=PE=1；再说明△DEF是等腰直角三角形，然后再利用勾股定理计算得到DE=EF= 10 ；如图2，由DC//AB可得△DGC∽△FGA，列比例式可求FG和CG的长，从而得EG的长；然后再根据AGHF是等腰直角三角形，求得GH和FH的长；利用DE∥GM证明△DEN∽△MNH，则 DEMH=ENNH 可得EN= 103 ，然后计算出△EMN各边的长，最后求周长即可.
8．【答案】C
【解析】【解答】解：①∵DE//AC，AE//BD，
∴四边形DEAO是平行四边形，
∵四边形ABCD是矩形，
∴OA=OD，
∴四边形DEAO为菱形，故①正确；
②当△AOB是等边三角形时，AE=AB才能成立，故②错误；
③当△AOB是等边三角形时，∠BAE=120°才能成立，故③错误；
④如图，设AC与BE交于点F，
∵∠BED=90°，
∴DE⊥BE，
∵DE//AC，
∴AC⊥BE，
∵O是矩形ABCD对角线BD的中点，
∴F是BE的中点，
∴AF是BE的垂直平分线，
∴AB=AE，
∵四边形DEAO为菱形，
∴DE=AE，
∵四边形ABCD是矩形，
∴AB=DC，∠BCD=90°，AD=BC，
∴DE=DC，
在Rt△BDE和Rt△BDC中，
BD=BDDE=DC，
∴Rt△BDE≌Rt△BDC(HL)，
∴BE=BC，
∴AD=BE.
∴说法正确的是①④.
故答案为：C.
【分析】由题意可得四边形DEAO是平行四边形，根据矩形的性质可得OA=OD，然后根据菱形的判定定理可判断①；根据等边三角形的性质可判断②③；设AC与BE交于点F，易得AC⊥BE，AF是BE的垂直平分线，则AB=AE，根据菱形的性质可得DE=AE，根据矩形的性质可得AB=CD，∠BCD=90°，AD=BC，则DE=DC，证明△BDE≌△BDC，得到BE=BC，则AD=BE，据此判断④.
9．【答案】B
【解析】【解答】 解：如图，连接CC′，交BD于点M，过点D作DH⊥BC′于点H，
∵AD=AC'=2，D是AC边上的中点，
∴DC=AD=2，
由翻折知，△BDC≌△BDC′，BD垂直平分CC′，
∴DC=DC′=2，BC=BC′，CM=C′M，
∴AD=AC'=DC′=2，
∴△ADC′为等边三角形，
∴∠ADC=∠AC′D=∠C′AC=60°，
∵DC=DC′，
∴∠DCC′=∠DC′C= 12 ×60°=30°，
在Rt△CDM中，∠DC′C=30°，DC′=2，
∴DM=1，C′M= 3 DM= 3 ，
·.BM=BD-DM=3-1=2，
在Rt△BMC中，BC′= BM2+C'M2=22+(3)2=7
∵SΔBDC'=12BC'⋅DH=12BD⋅CM
∴7DH=3×3
∴.BM=BD-DM=3-1=2，
在Rt△C'DM中， BC'=BM2+C'M2=22+(3)2=7
∵SΔBDC'=12BC'⋅DH=12BD⋅CM
∴7DH=3×3
∴DH=3217
故答案为：B.
【分析】连接CC′，交BD于点M，过点D作DH⊥BC于点H，由翻折知，△BDC≌△BDC’，BD垂直平分CC，证△ADC为等边三角形，利用解直角三角形求出DM=1，CM= 3DM = 3 ，BM=2，在Rt△BMC'中，利用勾股定理求出BC′的长，在△BDC中利用面积法求出DH的长.
10．【答案】A
【解析】【解答】解：由题意知△BEF是等边三角形， 作FH⊥BE于点H，如图，
∵△BEF是等边三角形，
∴ ∠BEF＝60°，BE＝EF＝BF，
∵FH⊥BE，
∴∠FHE＝90°，
∴FH＝BEsin∠BEF=BEsin60°＝32BE，
∴S△BEF=12BE·FH=34BE2，
设△BEF边长为b，则AC＝b，△BCD边长为a ，△BGH边长为c，则AB＝c，
S△BEF=34b2，
同理可得S△BCD=34a2，S△BGH=34c2，
∴S四边形EGHF=S△BGH−S△BEF=34c2−34b2=34(c2−b2)，
S四边形GDCH=S△BCD−S△BGH=34a2−34c2=34(a2−c2)，
∵△ABC是直角三角形，
∴b2+c2=a2，
∴b2=a2−c2，
∴S四边形EGHFS四边形GDCH =c2−b2a2−c2=c2−b2b2＝16164 ，
∴c2b2=22564，
∴cb=158，
设c＝15k，b＝8k，
则a=c2+b2=17k ，
∴sin∠ABC＝ba=8k17k=817 .
故答案为：A.
【分析】由题意知△BEF是等边三角形，作FH⊥BE于点H，根据等边三角形的性质可得 ∠BEF＝60°，BE＝EF＝BF，则∠FHE＝90°，根据三角函数的概念表示出FH，得到S△BEF，设△BEF边长为b，则AC＝b，△BCD边长为a ，△BGH边长为c，则AB＝c，表示出S△BEF、S△BCD、S△BGH，根据S四边形EGHF=S△BGH-S△BEF，S四边形GDCH=S△BCD-S△BGH表示出S四边形EGHF，S四边形GDCH，由勾股定理可得b2=a2-c2，代入求解可得cb=158，设c＝15k，b＝8k，由勾股定理可得a，然后根据三角函数的概念进行计算.
11．【答案】A
【解析】【解答】解：如图，过点A作AD⊥BC，交GH于点k，则AK⊥GH，
∵S正方形EFGH=4， ∴GH=GE=KD=2，
在正方形EFGH中，GH∥BC，
∴△AGH∽△ABC，
∴GHBC=AKAD，即26=AD-2AD，
解得AD=3，
过点A作直线a∥BC，作点C关于直线a的对称点C'，连接BC'交直线a于点A'，连接A'C ，则A'C=A'C'
此时A'C +A'B 的值最小，即为BC'，
由作图得∠BCC'=90°，CC'=2AD=6，
∴BC'=BC2+CC'2=62+62=62，
即AB+AC的最小值为62；
故答案为：A.
【分析】过点A作AD⊥BC，交GH于点K，则AK⊥GH，由正方形的性质及面积可得GH=GE=MD=2，GH=GE=KD=2，GH∥BC，利用平行线可证△AGH∽△ABC，利用相似三角形的性质可求出AD的长，过点A作直线a∥BC，可知点A在直线a上运动，作点C关于直线a的对称点C'，连接BC'交直线a于点A'，可知此时A'C +A'B 的值最小，即为BC'，利用勾股定理求出BC'的长，即得结论.
12．【答案】C
【解析】【解答】解：如图，
①以A为圆心，AB为半径画圆，交直线AC有二点M1，M2，交BC有一点M3，（此时AB=AM）；②以B为圆心，BA为半径画圆，交直线BC有二点M5，M4，交AC有一点M6（此时BM=BA）.③AB的垂直平分线交AC一点M7（MA=MB），交直线BC于点M8；
∴符合条件的点有8个。
故答案为：C。
【分析】根据等腰三角形的两腰相等，故需要分类讨论：①以点A为等腰三角形的顶角的顶点，AB为腰；②以点B为等腰三角形的顶角的顶点，AB为腰；③以点M为等腰三角形的顶角的顶点，AB为等腰三角形的底边，三种情况一一判断即可得出答案。
13．【答案】3+5
【解析】【解答】解：∵四边形ABCD为矩形，
∴∠B=∠C=90°，
∵∠A D' E=∠D=90°，
∴∠A D'B +∠E D'C =90°，∠E D'C+∠D'EC =90°，
∴∠A D'B=∠D'EC ，
∴△C D'E∽△BAD' ，
∴D'EAD'=CD'BA ，
∵C D' =DF，A D'=AD ， D'E=DE ，
∴DEAD=DFBA ，
∵∠EDF=∠BAD=90°，
∴△EDF∽△DAB，
∴∠FED=∠ADB，
∵∠ADB+∠BDC=90°，
∴∠FED+∠BDC=90°，
∴EF⊥BD，
又∵D'E ∥BD，A D'⊥D'E ，
∴BD⊥A D' ，
∴四边形HGE D' 是矩形，
∴HG=E D' =DE=2，
设EC=y，C D'=x ，
易得△EGD≌△ D'CE ，
∴DG=CE=y，EG=C D' =H D'=x ，
∵D'E ∥BD，
∴∠E D'C=∠D'BH ，
∵∠C=∠BH D'=90° ，
∴△BH D' ∽△ D'CE，
∴BHCD'=HD'EC ，
∴BHx=xy ，
即BH= x2y ，
∴BD=BH+GH+DG= y+2+x2y ，
易得：△DFE∽△CE D' ，
∴DECD'=DFEC
即 2x=xy ，
∴x2=2y ，
∵x2+y2=4 ，
∴y2+y−4=0 ，
∴y=−1+5 或 −1−5 （舍去），
∴BD= −1+5+3+2=3+5 .
所以答案为 3+5 .
【分析】首先证明出△C D' E∽△BA D' ，然后得出 D'EAD'=CD'BA ，进一步再证明△EDF∽△DAB，从而结合题意得出EF⊥BD，然后证明出四边形HGE D' 是矩形，得出HG=E D' =DE=2，之后设EC=y，C D' =x，通过△BH D' ∽△ D'CE ，表示出BD，然后再通过△DFE∽△CE D' 建立方程求出正确的y的值，进而计算求出BD即可.
14．【答案】94
【解析】【解答】解：如图，连接EF，作MN⊥HN于点N，
∵ 在矩形ABCD内放入四个小正方形和两个小长方形后形成中心对称图形，
∴△MNH≌△HKE≌△ESP，△MNH∽△FME，
∴MNNH=FMEM=12，
∴ADAB=4+2+1+22+1+1=94.
故答案为：94.
【分析】连接EF，作MN⊥HN于点N，根据中心对称的性质及相似三角形的判定可证△MNH≌△HKE≌△ESP，△MNH∽△FME，利用相似三角形的性质即可求解.
15．【答案】(−45，85)
【解析】【解答】解：如图，过点P作 PD⊥AB ，过点C作 CE⊥AB ，延长EC交圆C于点F，过点F作 FG⊥y 轴，连接AC
则 SΔPAB=12AB⋅PD
要使 ΔPAB 的面积最大，则PD需最大
由直线与圆的关系得，当点P与点F重合时，PD取得最大值，最大值为 EF
由题意得， OC=CF=1
直线 y=43x−3 ，令 x=0 得 y=−3 ，则 OB=3
令 y=0 得 43x−3=0 ，解得 x=94 ，则 OA=94
∴AB=OB2+OA2=32+(94)2=154，BC=OB+OC=3+1=4
∵SΔABC=12OA⋅BC=12AB⋅CE
∴12×94×4=12×154⋅CE ，解得 CE=125
∴BE=BC2−CE2=42−(125)2=165
在 ΔBCE 和 ΔFCG 中， ∠BCE=∠FCG∠BEC=∠FGC=90°
∴ΔBCE∼ΔFCG
∴BCFC=BEFG=CECG ，即 41=165FG=125CG
∴FG=165×14=45，CG=125×14=35
∴OG=OC+CG=1+35=85
则点F的坐标为 (−45，85) ，即当 ΔPAB 的面积最大时，点P的坐标为 (−45，85)
故答案为： (−45，85) ．
【分析】过点P作 PD⊥AB ，过点C作 CE⊥AB ，延长EC交圆C于点F，过点F作 FG⊥y 轴，连接AC，先根据直线与圆的关系求出当 ΔPAB 的面积最大时，点P的位置，再利用直线的解析式、勾股定理求出OA、OB、AB的长，然后根据三角形相似的判定定理与性质即可得．
16．【答案】180°−α2n−1
【解析】【解答】解：折叠1次可得：∠ABR1=α2，
折叠2次可得：∠R1BR2=12×α2，
折叠3次可得：∠R2BR3=12×12×α2，
折叠4次可得：∠R3BR4=12×12×12×α2，
…
由折叠的性质折叠n次可得∠Rn−1BRn=12×12×...×12α=α2n，
如图：
在四边形BRnNM中内：∠BRnN=360°−90°−90°−α2n=180°−α2n
∴∠ARnN=∠BRnN−∠Rn−1RnB=∠BRnN−∠Rn−1BRn=180°−α2n−α2n=180°−α2n−1.
故答案为：180°−α2n−1．
【分析】根据题意，分别表示出∠ABR1，∠R1BR2，∠R2BR3，∠R3BR4，，得规律∠Rn−1BRn=α2n.于是在四边形BRnNM中内，由内角和定理求得∠BRnN，利用角的和差即可得到∠ARnN的值.
17．【答案】35
【解析】【解答】如图，延长FP交AB于M，
当FP⊥AB时，点P到AB的距离最小，
∵∠C＝90°，AC＝3，BC＝4，
∴AB＝5，（勾股定理）
∵∠A＝∠A，∠AMF＝∠C＝90°，
∴△AFM∽△ABC，
∴AFAB=FMBC ，即 25=FM4
解得，FM＝ 85 ，
由折叠的性质可知，FP＝FC＝1，
∴PM＝ 35 ，
故答案为： 35 .
【分析】如图，延长FP交AB于M，当FP⊥AB时，根据点到直线的距离，垂线段最短可知：点P到AB的距离最小，根据勾股定理算出AB的长，进而判断出△AFM∽△ABC，根据相似三角形对应边成比例得出AFAB=FMBC，根据比例式算出FM的长，由折叠的性质可知，FP＝FC＝1，进而根据线段的和差算出答案。
18．【答案】15
【解析】【解答】解： ∵ 四边形 ABCD 是正方形
∴∠D=∠DAB=90° ， AD=BA
∵ 折叠
∴AH⊥BF
∴∠AHB=90°
∴∠ABF+∠BAH=90°
∵ ∠BAH+∠DAE=90°
∴∠DAE=∠ABF
∴△DAE≌△ABF （ASA）
∴AE=BF ， AF=DE
∵ AB=4 ， DE=4
∴ AF=3 ， BF=AB2+AF2=32+42=5
∴ AH=AF⋅ABBF=3×45=125
∴AG=2AH=245
∴ GE=AE−AG=5−245=15
故答案为 15
【分析】根据折叠图形的性质和正方形的性质得出有关角和边相等，利用AAS证明△AED≌△BFA，可知AE=BF，AF=DE，再利用勾股定理求出BF，然后由等面积法求得AH的长，由折叠的性质可知AG=2AH，最后利用线段的和差关系即可求得GE的长.
19．【答案】解：如图，过点B作BA∥CD，过点D作AD∥BC，AB与AD交于点A，连接AE，
∵BA∥CD，AD∥BC，
∴∠ABC+∠BCD＝180°，∠ADC+∠BCD＝180°，
∴∠ABC＝∠ADC＝90°，
∴四边形ABCD是矩形，
又∵CD＝CB，
∴四边形ABCD是正方形，
∴AB＝BC＝AD＝CD，
∵BE＝CE，
∴∠EBC＝∠ECB，
∴∠ABC﹣∠EBC＝∠BCD﹣∠ECB，
∴∠ABE＝∠DCE，
∴△ABE≌△DCE（SAS），
∴AE＝DE，
∵DE＝DC，
∴DE＝AE＝AD，
∴△ADE是等边三角形，
∴∠ADE＝60°，
∴∠CDE＝30°．
【解析】【分析】过点B作BA∥CD，过点D作AD∥BC，AB与AD交于点A，连接AE，可证明四边形ABCD是正方形，可得AB=BC=AD=CD，由“SAS”可证△ABE≌△DCE，可得AE=DE，可证△ADE是等边三角形，即可求解。
20．【答案】解：（1）（2）
（3）三角形的一边长与该边上的高相等的直角三角形或锐角三角形；
（4）对角线互相垂直．
【解析】【分析】（1）图2中将三角形的三个角分别向三角形内部进行折叠即可；
（2）图3中只要使三角形一边上的高等于该边长即可；
（3）利用折叠后的两个重合的正方形可知，三角形一边长的一半和这一边上的高的一半都等于正方形的边长，所以三角形的一边和这边上的高应该相等；
（4）如果一个四边形能折叠成叠加矩形，可以将四边形的四个角分别向四边形内部折叠即可得到该结果，折痕应经过四边中点，而连接四边形各边中点得到矩形的话，该四边形的对角线应互相垂直．
21．【答案】（1）FAE|△EAF|GF
（2）证明：延长CF，作∠4=∠1，
∵将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=12∠DAB，
∴∠1+∠2=∠3+∠5，∠2+∠3=∠1+∠5，
∵∠4=∠1，
∴∠2+∠3=∠4+∠5，
∴∠GAF=∠FAE，
∵在△AGB和△AED中，
∠4=∠1AB=AD∠ABG=∠ADE，
∴△AGB≌△AED(ASA)，
∴AG=AE，BG=DE，
∵在△AGF和△AEF中，
AG=AE∠GAF=∠EAFAF=AF，
∴△AGF≌△AEF(SAS)，
∴GF=EF，
∴DE+BF=EF；
（3）当∠B与∠D满足∠B+∠D=180°时，可使得DE+BF=EF．
【解析】【解答】解：（1）将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，
由旋转可得： AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，
∴∠ABG+∠ABF=90°+90°=180°，
因此，点G，B，F在同一条直线上．
∵∠EAF=45°
∴∠2+∠3=∠BAD−∠EMF=90°−45°−45°．
∵∠1=∠2，
∴∠1+∠3=45°．
即∠GAF=∠FAE， ．
又AG=AE，AF=AF
∴△GAF≌ △EAF．
∴GF=EF，故DE+BF=EF．
故答案为：FAE，△EAF，GF；
（3） 当∠B与∠D满足∠B+∠D=180°时，可使得DE+BF=EF，
如图延长CF，作∠2=∠1，
∵∠ABC+∠D=180°，∠ABC+∠ABG=180°，
∴∠D=∠ABG，
∴△AGB≌△AED（ASA），
∴BG=DE，AG=AE，
∵∠EAF=∠12DAB，
∴∠EAF=∠GAF，
∴△AGF≌△AEF（SAS），
∴GF=EF，
∴DE+BF=EF，
【分析】（1）由角之间的数量关系可得∠GAF=∠FAE，根据SAS证明△AGF≌△AEF，利用全等三角形的性质即可求解；
（2） 延长CF，作∠4=∠1，先证△AGB≌△AED（ASA），再证△AGF≌△AEF（SAS），可得FG=EF，再证△AGF≌△AEF(SAS)， 可得GF=EF，利用线段的和差即可求解；
（3）当∠B+∠D=180°时，可得∠D=∠ABG，先证△AGB≌△AED（ASA），再证△AGF≌△AEF（SAS），可得GF=EF，利用线段的和差即可求解。
22．【答案】（1）解：∵在△EDF中，∠EDF=90°，DE=DF，
∴∠E=∠DFE=45°，
∵DN⊥DM，
∴∠MDN=∠EDF=90°，
∴∠MDN−∠MDF=∠EDF−∠MDF，即∠NDF=∠MDE，
又∵ND=MD，FD=ED，
∴△NDF≌△MDE(SAS)，
∴∠NFD=∠MED=45°，
∴∠EFN=∠NFD+∠DFE=90°
（2）解：FM2+EM2=2DM2，证明如下：
如图所示，连接NF，
同理可证△NDF≌△MDE，
∴∠NFD=∠MED=45°，NF=ME，
∴∠EFN=∠NFD+∠DFE=90°；
在Rt△DNM中，由勾股定理得MN=ND2+DM2=2DM，
在Rt△MNF中，由勾股定理得NF2+FM2=MN2，
∴FM2+EM2=(2DM)2，
∴FM2+EM2=2DM2
（3）解：如图所示，过点D作DH⊥DM且DH=DM，连接MH，FH，
∴∠MDH=∠FDE=90°，∠DMH=∠DHM=45°，
∴∠MDH+∠MDF=∠FDE+∠MDF，即∠MDE=∠HDF，
又∵DM=DH，DF=DE，
∴△MDE≌△HDF(SAS)，
∴ME=HF，
∵DM=DH=5，
∴HM=DM2+DH2=52，
∵∠HMF=∠DMH+∠DMF=90°，
∴HF=HM2+MF2=36，
∴ME=HF=36
【解析】【分析】（1）可根据SAS证明 △ NDF≌ △ MDE，从而得出∠NFD=∠MED=45°，进而得出∠EFN=90°；
（2） FM2+EM2=2DM2，由（1）知 △ NDF≌ △ MDE，且∠EFN=90°，FN=EM，根据勾股定理可得：FM2+FN2=MN2，再根据MN2=2DM2，从而得出FM2+EM2=2DM2；
（3） 如图所示，过点D作DH⊥DM且DH=DM，连接MH，FH， 首先证明 △ MDE≌ △ HDF，得出ME=HF，在Rt △ HDM中，根据勾股定理，可得： ∴HM=DM2+DH2=52， 在Rt △ HMF中，可得：HF=HM2+MF2=36， 从而得出EM=36.
23．【答案】（1）证明：∵∠C＝∠D＝∠AEB＝90°，
∴∠BEC+∠AED＝∠AED+∠EAD＝90°，
∴∠BEC＝∠EAD，
∴Rt△AED∽Rt△EBC，
∴AEEB=DECB．
（2）证明：如图1，过点G作GM⊥CD于点M，
由（1）可知EFEG=DEGM，
∵EFEG=AEEB，AEEB=DECB，
∴DEGM=DECB，
∴BC＝GM，
又∵∠C＝∠GMH＝90°，∠CHB＝∠MHG，
∴△BCH≌△GMH（AAS），
∴BH＝GH，
（3）证明：如图2，在EG上取点M，使∠BME＝∠AFE，
过点C作CN∥BM，交EG的延长线于点N，则∠N＝∠BMG，
∵∠EAF+∠AFE+∠AEF＝∠AEF+∠AEB+∠BEM＝180°，∠EFA＝∠AEB，
∴∠EAF＝∠BEM，
∴△AEF∽△EBM，
∴AEBE=EFBM，
∵∠AEB+∠DEC＝180°，∠EFA+∠DFE＝180°，
而∠EFA＝∠AEB，
∴∠CED＝∠EFD，
∵∠BMG+∠BME＝180°，
∴∠N＝∠EFD，
∵∠EFD+∠EDF+∠FED＝∠FED+∠DEC+∠CEN＝180°，
∴∠EDF＝∠CEN，
∴△DEF∽△ECN，
∴DEEC=EFCN，
又∵AEEB=DEEC，
∴EFBM=EFCN，
∴BM＝CN，
又∵∠N＝∠BMG，∠BGM＝∠CGN，
∴△BGM≌△CGN（AAS），
∴BG＝CG．
【解析】【分析】（1） 先证出Rt△AED∽Rt△EBC，再利用相似三角形的性质可得AEEB=DECB；
（2）过点G作GM⊥CD于点M，先利用“AAS”证出 △BCH≌△GMH ，再利用全等三角形的性质可得 BH＝GH；
（3）在EG上取点M，使∠BME＝∠AFE，先证出 △AEF∽△EBM， 可得AEBE=EFBM，再证出 △DEF∽△ECN， 可得DEEC=EFCN，再结合AEEB=DEEC可得EFBM=EFCN，可得 BM＝CN， 再结合“AAS”证出 △BGM≌△CGN ，可得 BG＝CG．
24．【答案】（1）解：∵AB=AC，AD=AE，
∴∠ABC=∠ACB，∠EDA=∠DEA.
∴∠BDA=∠CEA.
在△ABD和△ACE中，∠ADB=∠AEC，∠B=∠C，AB=AC，
∴△ABD≌△ACE(AAS).
（2）解：证明：如图所示，在AB上截取AD=AE，连接CE.
∵AC平分∠DAB，
∴∠EAC=∠DAC.
在△ADC和△AEC中，AD=AE，∠DAC=∠EAC，AC=AC，
∴△ADC≌△AEC(SAS).
∴EC=DC，∠ADC=∠AEC.
∵∠ABC+∠ADC=180°=∠CEB+∠AEC，
∴∠ABC=∠CEB.
∴CB=CE.
∴CD=CB.
（3）BF的长为3.5 cm.
【解析】【解答】解：（3）∵FE=BE，
∴∠EBF=∠EFB，
∵△ABC是等边三角形，
∴∠ABC=∠C=60°，
∴∠EBF=∠EBA+60°，∠EFB=∠FEC+60°，
∴∠EBA=∠FEC，
在AC上取点M，连接MF，使得FM=FC，如图，
∵∠ACB=60°，
∴△CFM是等边三角形，
∴∠CMF=60°，
∴∠BAE=∠EMF=120°，
∴△ABE≅△MEF(AAS)，
∴AE=MF，
∵FM=CF，
∴CF=AE=1.5cm，
∵BC=5cm，
∴BF=BC-CF=3.5cm，
故BF的长为3.5 cm.
【分析】（1）根据AB=AC，AD=AE，可得∠ABC=∠ACB，∠EDA=∠DEA，进而得到∠BDA=∠CEA，利用AAS可证明△ABD≌△ACE；
（2） 在AB上截取AD=AE，连接CE ，根据角平分线的性质可得 ∠EAC=∠DAC ，进而证明△ADC≌△AEC，利用全等三角形的性质有EC=DC，∠ADC=∠AEC，结合已知条件利用平角的定义求得∠ABC=∠CEB，得到CB=CE，从而得出结论；
（3）利用AAS证明△ABE≅△MEF，根据全等三角形的性质可得AE=MF，从而求解.