数学：江苏省南通市崇川区2024年中考一模模拟试题（解析版）

这是一份数学：江苏省南通市崇川区2024年中考一模模拟试题（解析版），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 下列各数中，是无理数的是（ ）
A. B. C. D. 0
【答案】B
【解析】，，0是有理数；是无理数．
故选：B．
2. 据统计，2024年一季度全国农村居民人均可支配收入6596元，将6596用科学记数法表示为（ ）
A. B.
C. D.
【答案】A
【解析】依题意，将6596用科学记数法表示为，
故选：A．
3. 如图所示的四个几何体中，俯视图是三角形的是（ ）
A. B.
C. D.
【答案】A
【解析】三棱柱的俯视图是三角形，故选项A符合题意；
圆柱的俯视图是圆，故选项B不符合题意；
四棱锥的俯视图四边形中间有一个点，故选项C不符合题意；
圆锥的俯视图是圆中间有一点，故选项D不符合题意．
故选：A．
4. 下列调查中，适宜采用抽样调查的是（ ）
A. 调查某班学生的身高情况
B. 调查某批汽车的抗撞击能力
C. 调查亚运会米游泳决赛运动员兴奋剂的使用情况
D. 调查一架“歼”隐形战斗机各零部件的质量
【答案】B
【解析】A．调查某班学生的身高情况适合采用全面调查，故此选项不符合题意；B．调查某批汽车抗撞击能力适宜采用抽样调查，故此选项符合题意；C．调查亚运会 米游泳决赛运动员兴奋剂的使用情况适合采用全面调查，故此选项不符合题意；D．调查一架“歼 ”隐形战斗机各零部件的质量适合采用全面调查，故此选项不符合题意；故选B．
5. 在Rt△ABC中，∠C=90°，AC=3，BC=4，以AC所在直线为轴，把△ABC旋转1周，得到圆锥，则该圆锥的侧面积为（ ）
A 12πB. 15πC. 20πD. 24π
【答案】C
【解析】∵∠C=90°，AC=3，BC=4，∴AB==5，
以直线AC为轴，把△ABC旋转一周得到的圆锥的侧面积=×2π×4×5=20π．故选：C．
6. 已知是整数，当取最小值时，的值是( )
A. 5B. 6C. 7D. 8
【答案】A
【解析】∵，∴，
且与最接近的整数是5，∴当取最小值时，的值是5，故选A．
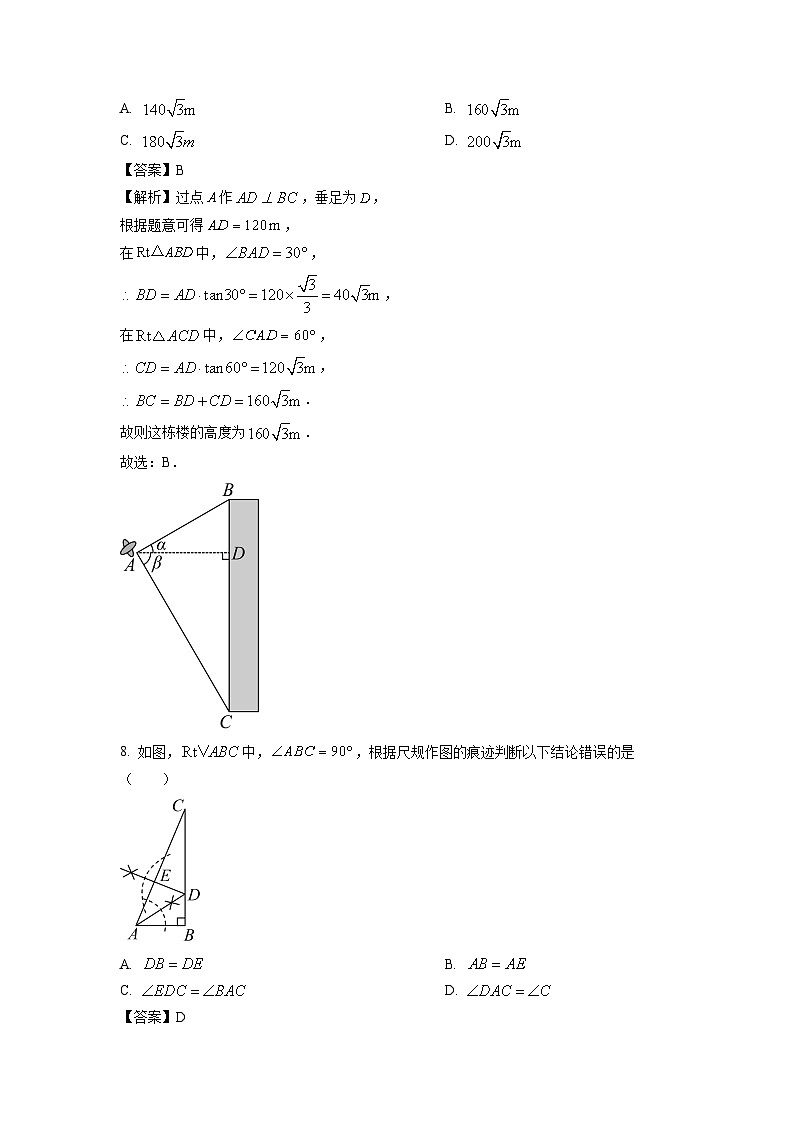
7. 如图，从航拍无人机看一栋楼顶部的仰角为，看这栋楼底部的俯角为，无人机与楼的水平距离为，则这栋楼的高度为（ ）

A. B.
C. D.
【答案】B
【解析】过点作，垂足为，
根据题意可得，
在中，，
，
在中，，
，
．
故则这栋楼的高度为．
故选：B．

8. 如图，中，，根据尺规作图的痕迹判断以下结论错误的是（ ）

A. B.
C. D.
【答案】D
【解析】由尺规作图可知，AD是∠CAB角平分线，DE⊥AC，
在△AED和△ABD中：
∵，∴△AED≌△ABD(AAS)，
∴DB=DE，AB=AE，选项A、B都正确，
又在Rt△EDC中，∠EDC=90°-∠C，
在Rt△ABC中，∠BAC=90°-∠C，
∴∠EDC=∠BAC，选项C正确，
选项D，题目中缺少条件证明，故选项D错误．
故选：D.
9. 如图（1），点P为菱形对角线上一动点，点E为边上一定点，连接，，．图（2）是点P从点A匀速运动到点C时，的面积y随的长度x变化的关系图象（当点P在上时，令），则菱形的周长为（ ）
A. B. C. 20D. 24
【答案】C
【解析】由图象可知：当时，即点与点重合，此时，
∴，
当时，此时点与点重合，即，连接，交于点，
则：，
∴，
∴，
∴，
∴，
∴菱形的周长为；
故选C．
10. 如图，平面直角坐标系xOy中，点A（，），点B（，）在双曲线上，且，分别过点A，点B作x轴的平行线，与双曲线分别交于点C，点D． 若△AOB的面积为，则的值为（ ）
A. B. C. D.
【答案】C
【解析】过点A作轴，交y轴于点E，过点B作轴，交x轴于点F，延长BF，交AC于点G，
∴四边形为矩形，
∵点A（，），点B（，）在双曲线上，
∴，，，
矩形面积
，
∵，
∴，
∴，
设，则，
∴，
∴，
∴，或，
∵，
∴不符合题意，经检验，是原方程的解，
∴，
根据题意，得，，
∴，，
∴，故选：C．
二、填空题（本大题共8小题，第11～12题每小题3分，第13～18题每小题4分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
11. 计算：=_____．
【答案】
【解析】．
故答案为：
12. 分解因式：=_________.
【答案】 (2x+3)(2x-3)
【解析】利用平方差公式得：(2x+3)(2x-3).
13. 已知正六边形的内切圆半径为，则它的周长为______．
【答案】
【解析】如图，连接、，；
六边形是边长等于正六边形的半径，设正六边形的半径为，
是等边三角形，
，
，
解得，
它的周长．
故答案为：．
14. 我国古代数学著作《九章算术》中有“共买鸡问题”：今有共买鸡，人出九，盈十一；人出六，不足十六．问人数，物价各几何？题意是：有若干人一起买鸡．如果每人出9文钱，就多出11钱；如果每人出6文钱；就相差16文钱．买鸡的人数、鸡的价钱各是多少？设有人，可列出方程为______________．
【答案】
【解析】设有人共同买鸡，根据题意得：
故答案为：
15. 如图，是的直径，点，在上．若，则__________度．

【答案】
【解析】如图所示，连接，

∵是直径，
∴，
∵，，
∴，
∴，
故答案为：．
16. 对于任意的，恒成立，则a的取值范围是 ________．
【答案】
【解析】由可得：，
当时，不等式解集为，
对于任意的，恒成立，
∴，解得：；∴，
当时，恒成立，满足题意；
当时，不等式的解集为，
∵对于任意的，恒成立，
∴，解得：，故符合题意；
综上所述，．
故答案为：．
17. 已知抛物线过点，两点，若线段的长不大于，则代数式的最小值是_________.
【答案】
【解析】∵抛物线y=ax2+4ax+4a+1（a≠0）过点A（m，3），B（n，3）两点，
∴，顶点为（-2,1）
∴由题意可知a>0,
∵线段AB的长不大于4，
∴4a+1≥3
∴a≥
∴a2+a+1的最小值为：（）2++1=；故答案为．
18. 如图，已知矩形的一边长为12，点P为边上一动点，且满足，则的取值范围是__________．
【答案】
【解析】①如图1，当点P与点A重合时，
∵四边形是矩形，
∴，
∵，
∴,即，
解得：，此时BC是满足题意的最大值；
②如图2，当点P是的中点时，此时最小，
过点B作于E，
设，则
∵，
∴，，
∴，解得：（舍）或，
∴．
∴此时是满足题意的最小值．
综上，．
故答案为：．
三、解答题（本大题共8小题，共90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19. （1）计算：；
（2）解方程：．
解：（1）；
（2）
，
检验，当时，，
所以是原分式方程的解．
20. 某校六年级200名学生参加了环保知识竞赛，已知竞赛得分都是整数，满分100分．随机抽取了部分学生的竞赛成绩作为一个样本，数据整理后分成6个小组，画出竞赛成绩的频数分布直方图，如图1所示（每个小组可包括最小值，不包括最大值），同时画出竞赛成绩等第的扇形统计图，如图2所示（设竞赛成绩为a分，为不合格、为合格，为良好，为优秀）．根据图中的信息回答下列问题：

（1）估计六年级参赛学生中成绩为良好的学生有________人；请把图1补画完整、补齐图2中缺失的数据；
（2）小明对统计图进行了研究，得出了如下结论：
①中位数一定落在80分—90分这一组内；
②众数一定落在80分—90分这一组内；
③仍有不合格的学生，该校环保知识宣传需进一步加强；
④从这两个统计图中能准确求出样本的平均数．
上述结论中错误的是________（填序号）．
（3）估计本次六年级参赛学生中荣获优秀的共有m人．学校“环保社团”决定：这m名学生都光荣的成为学校的小小环保“宣传员”，从中选派x人帮助本年级参赛得分60分以下的学生普及环保知识．经计算，x与的积恰好等于样本容量的15倍．你认为x的值取多少比较合理，为什么？
解：（1）∵，
∴，
∵，
六年级参赛学生中成绩为良好的学生有人；
∵良好占，
∴合格占
补全条形图如下：

（2）由个数据，第个，第个数据落在80分—90分这一组，故①正确；
众数是出现次数最多的数据，不一定落在80分—90分这一组内，故②不正确；
仍有不合格的学生，该校环保知识宣传需进一步加强；故③正确；
从这两个统计图中不能准确求出样本的平均数，故④不正确；
∴上述结论中错误的是②④；
（3）由（1）得：，样本容量为，
∴，
整理得：，
解得：，，
∵得分60分以下的学生有，
∴合理；
21. 如图，点A、B、C、D在一条直线上，，求证：．

解：∵，
∴，
即，
∵，
∴
∴，
∴，
∵，
∴四边形是平行四边形，
∴．
22. 如图，某校食堂实行统一配餐，为方便学生取餐，食堂开设了4个窗口，分别记为①、②、③、④，学生可以从这4个窗口中任意选取一个窗口取餐．

（1）若小明去食堂用餐时4个窗口都没有人，则小明选择在②号窗口取餐的概率是________；
（2）若小红和小丽-起去食堂用餐时4个窗口都没有人，求小红和小丽在相邻窗口取餐的概率．（请用画树状图或列表等方法说明理由）
解：（1）若小明去食堂用餐时4个窗口都没有人，则小明选择在②号窗口取餐的概率是，
故答案为：．
（2）画出树状图如图，

共有16种等可能结果，符合题意的有6种，
∴小红和小丽在相邻窗口取餐的概率为
23. 如图，Rt△ABC中，，，以AB为直径作⊙O交AC与点D，过点D的切线交BC于点E．
（1）求∠BED的度数；
（2）若，求图中阴影部分的面积．
解：（1）如图，连接OD，
∵DE与⊙O相切于点D，
∴
∵Rt△ABC中，，，
∴，
∴，
又∵，
∴；
（2）如图，连接OD，过点D作DF⊥AB于F，
∵，，
∵，∴，
∵Rt△OFD中，，
∴，
∴；
24. 某市在盐碱地种植海水稻获得突破性进展，小亮和小莹到海水稻种植基地调研．小莹根据水稻年产量数据，分别在直角坐标系中描出表示2017-2021年①号田和②号田年产量情况的点（记2017年为第1年度，横轴表示年度，纵轴表示年产量），如下图．
小亮认为，可以从y=kx+b(k>0) ，y=(m>0) ，y=−0.1x2+ax+c中选择适当的函数模型，模拟①号田和②号田的年产量变化趋势．
（1）小莹认为不能选．你认同吗？请说明理由；
（2）请从小亮提供的函数模型中，选择适当的模型分别模拟①号田和②号田的年产量变化趋势，并求出函数表达式；
（3）根据（2）中你选择的函数模型，请预测①号田和②号田总年产量在哪一年最大？最大是多少？
解：（1）认同，理由如下：
观察①号田的年产量变化：每年增加0.5吨，呈一次函数关系；
观察②号田的年产量变化：经过点（1，1.9），（2，2.6），（3，3.1），
∵1×1.9=1.9，2×2.6=5.2，1.9≠5.2，
∴不是反比例函数关系，
小莹认为不能选是正确；
（2）由（1）知①号田符合y=kx+b(k>0)，
由题意得，解得：，
∴①号田的函数关系式为y=0.5x+1(k>0)；
检验，当x=4时，y=2+1=3，符合题意；
②号田符合y=−0.1x2+ax+c，
由题意得，解得：，
∴②号田的函数关系式为y=−0.1x2+x+1；
检验，当x=4时，y=-1.6+4+1=3.4，符合题意；
（3）设总年产量为w，
依题意得：w=−0.1x2+x+1+0.5x+1=−0.1x2+1.5x+2
=−0.1(x2-15x+-)+2
=−0.1(x-7.5)2+7.625，
∵−0.1<0，∴当x=7.5时，函数有最大值，
∴在2023年或2024年总年产量最大，最大是7.6吨．
25. 已知矩形中，E是的中点，于点F．
（1）如图1，若，求的值；
（2）如图2，连接交于点G，若，求的值；
（3）如图3，延长交于点G，若G点恰好为的中点，过A作交于K，设的面积为，的面积为，求的值．
解：（1）是的中点，
，
四边形是矩形，
，，，
，
，
，
，
，
；
（2）延长交的延长线于，连接、，如图2所示：
四边形是矩形，
，，，
，
，
，
是的中点，
，
，
四边形是平行四边形，
，
四边形是菱形，
，，，
，
，
，
，
，
，
，
，
；
（3）过作于，交于，作于，如图3所示：
则，，，
是的中点，是的中点，
，，
四边形是矩形，
，，，
，
，
，
，
，
，即，
，
四边形是正方形，
，
设，
则，
，，
，
，
，
，
，即，
解得：，，
，
，
，
，
设，则，
，，
，，
，
又，
，
，即，
解得：，
，
，
解得：，
，
的面积为，的面积为，
；
故答案为：．
26. 定义：若函数的图象上至少存在一个点，该点关于x轴的对称点落在函数的图象上，则称函数，为关联函数，这两个点称为函数，的一对关联点．例如，函数与函数为关联函数，点和点是这两个函数的一对关联点．
（1）判断函数与函数是否为关联函数？若是，请直接写出一对关联点；若不是，请简要说明理由；
（2）若对于任意实数，函数与始终为关联函数，求的值；
（3）若函数与函数(，为常数)为关联函数，且只存在一对关联点，求的取值范围．
解：（1）函数与函数是关联函数
依题意，设和是与函数这两个函数的一对关联点，
∴，解得：或，
∴和或和是这两个函数的一对关联点；
（2）∵对于任意实数，函数与始终为关联函数，
∴，
，
即，
∴，，
∴；
（3）与函数(，为常数)为关联函数，且只存在一对关联点，
设和是这对函数的关联点，
∴，
即关于的方程，有两个相等的实数根，
∴，
，
∴，
∴，
∵，
∴．