2023-2024学年安徽省黄山市八年级（下）期中数学试卷

这是一份2023-2024学年安徽省黄山市八年级（下）期中数学试卷，共14页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

1．（3分）若在实数范围内有意义，则x的取值范围是（ ）
A．x＞0B．x≥0C．x≥﹣2D．x＞﹣2
2．（3分）下列各式中，正确的是（ ）
A．B．C．D．
3．（3分）下列计算正确的是（ ）
A．B．C．D．
4．（3分）在平行四边形ABCD中，∠A+∠C＝160°，则∠B的度数是（ ）
A．60°B．80°C．100°D．160°
5．（3分）以下列各组数为边长，能构成直角三角形的是（ ）
A．，，B．2，3，4C．2，2，5D．
6．（3分）下列命题的逆命题是假命题的是（ ）
A．矩形的对角线相等
B．对角线相等的四边形是正方形
C．对角线互相平分的四边形是平行四边形
D．菱形的对角线互相垂直平分
7．（3分）如图，在矩形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片，则图中空白部分的面积为（ ）
A．（8﹣4）cm2B．（4﹣2）cm2
C．（16﹣8）cm2D．（﹣12+8）cm2
8．（3分）如图，正方形ABCD是由9个边长为1的小正方形组成，每个小正方形的顶点都叫格点，点E，F都在格点上，连接AE，AF，则∠EAF=​（ ）
A．30°B．45°C．60°D．75°
9．（3分）如图，在△ABC中，D，E分别是边AB，AC的中点，F是DE延长线上一点，且∠AFC=90°，若BC=m,DF=n（n＞m），则AC=（ ）​
A．n﹣mB．C．2n﹣mD．2m﹣n
10．（3分）如图，△ABC中，∠ACB=90°，AC=4，BC=3，将△ADE沿DE翻折，使点A与点B重合，则AE的长为（ ）
A．B．3C．D．
二、填空题（本大题共6小题，每小题3分，满分18分.请在答题卷的相应位置作答.）
11．（3分）已知a，b都是实数．若+（b﹣2）2＝0，则a﹣b＝ ．
12．（3分）已知，则x﹣20232＝ ．
13．（3分）如图，菱形ABCD中，AC=8，BD=10，则CD边上的高AE= .
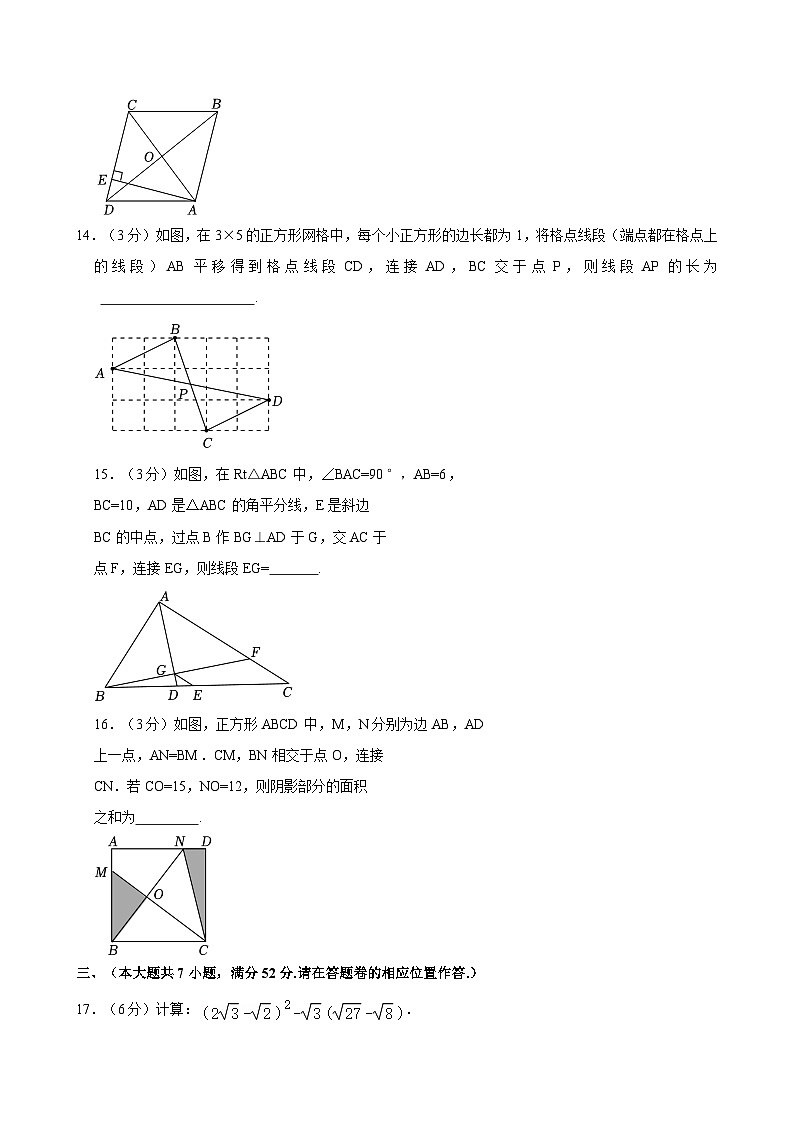
14．（3分）如图，在3×5的正方形网格中，每个小正方形的边长都为1，将格点线段（端点都在格点上的线段）AB平移得到格点线段CD，连接AD，BC交于点P，则线段AP的长为 .
15．（3分）如图，在Rt△ABC中，∠BAC=90°，AB=6，
BC=10，AD是△ABC的角平分线，E是斜边
BC的中点，过点B作BG⊥AD于G，交AC于
点F，连接EG，则线段EG= .
16．（3分）如图，正方形ABCD中，M，N分别为边AB，AD
上一点，AN=BM．CM，BN相交于点O，连接
CN．若CO=15，NO=12，则阴影部分的面积
之和为 .
三、（本大题共7小题，满分52分.请在答题卷的相应位置作答.）
17．（6分）计算：．
18．（6分）先化简，再求值：（+）•，其中m＝-1
19．（6分）如图，在△ABC中，AB=4，BC=，点D在AB上，且BD=1，CD=2．
（1）求证：CD⊥AB；
（2）求AC的长．
20．（6分）如图，正方形网格中的每个小正方形的边长都是1个单位长度，每个小格的顶点叫做格点．
（1）在图1中以格点为顶点画一个面积为10的正方形；
（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2，，．
21．（8分）二次根式的计算中，有一种方法叫做“分子有理化”，即分母和分子同时乘以一个适当的因式，从而消除分子中的根式．
比如：．
“分子有理化”可以用来比较某些二次根式的大小，也可以用来处理一些代数式的最值问题．
例如：比较和的大小．
解：，．
因为，
所以，即．
再例如，求代数式的最大值．做法如下：
解：由x+2≥0且x﹣2≥0可知：x≥2，而
＝
当x＝2时，分母有最小值2
利用上面的方法，完成下面问题：
（1）比较和的大小；
（2）求代数式的最大值．
22．（10分）如图，在平行四边形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF=BE，连接DF．
（1）求证：四边形ADFE为矩形；
（2）连接OF，若AD=3，EC=2，∠ABF=60°，求OF的长．
23．（10分）在Rt△ABC中，M是斜边AB的中点，点D在直线AB外，且DM=AM，连接AD，BD．
（1）如图1，求证：AD⊥BD；
（2）如图2，E是边AC上一点，且ME⊥AD，DE∥AB．
求证：四边形AEDM是菱形．
2023-2024学年安徽省黄山市八年级（下）期中数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，满分30分.在每小题所给的四个选项中，只有一项是正确的，请在答题卷的相应位置作答.）
1．【答案】C
【解答】解：由题意得：x+2≥0，
解得：x≥﹣3．
故选：C．
2．【答案】C
【解答】解：∵＜＜，＝4，，
∴4＜＜6．
故选：C．
3．【答案】D
【解答】解：A、与不是同类二次根式，原计算错误；
B、3﹣＝6，不符合题意；
C、÷3＝，不符合题意；
D、＝2，符合题意，
故选：D．
4．【答案】C
【解答】解：∵四边形ABCD是平行四边形，
∴∠A＝∠C，AD∥BC，
∴∠A+∠B＝180°，
∵∠A+∠C＝160°，
∴∠A＝80°，
∴∠B＝100°．
故选：C．
5．【答案】D
【解答】解：A、∵（）2+（）2≠（）2，∴不能构成直角三角形，不符合题意；
B、∵22+22≠43，∴不能构成直角三角形，不符合题意；
C、∵2+2＝6＜5，不符合题意；
D、∵25+（）2＝82，∴能构成直角三角形，符合题意，
故选：D．
6．【答案】A
【解答】解：“矩形的对角线相等”的逆命题是“对角线相等的四边形是矩形”，逆命题是假命题；
“对角线相等的四边形是正方形”的逆命题是“正方形的对角线相等”，逆命题是真命题；
“对角线互相平分的四边形是平行四边形”的逆命题是“平行四边形的对角线互相平分”，逆命题是真命题；
“菱形的对角线互相垂直平分”的逆命题是“对角线互相垂直平分的四边形是菱形”，逆命题是真命题；
故选：A．
7．【答案】D
【解答】解：∵两张正方形纸片的面积分别为16cm2和12cm2，
∴它们的边长分别为＝2cm，cm，
∴AB＝4cm，BC＝（3，
∴空白部分的面积＝（2+4）×4﹣12﹣16，
＝6+16﹣12﹣16，
＝（﹣12+8）cm2．
故选：D．
8．【答案】B
【解答】解：连接EF，
∵AE＝＝，EF＝＝＝，
∴AE3+EF2＝AF2，AE＝EF，
∴△AEF是等腰直角三角形，
∴∠EAF＝45°．
故选：B．
9．【答案】C
【解答】解：∵D，E分别是边AB，BC＝m，
∴DE＝BC＝m，
∴EF＝DF﹣BC＝n﹣m，
∵∠AFC＝90°，
∴AC＝2EF＝2n﹣m．
故选：C．
10．【答案】D
【解答】解：设AE＝BE＝x，则CE＝4﹣x，
在Rt△BCE中，BE2＝CE6+BC2，
即x2＝（8﹣x）2+35，
解得x＝，
故选：D．
二、填空题（本大题共6小题，每小题3分，满分18分.请在答题卷的相应位置作答.）
11．【答案】﹣3．
【解答】解：∵+（b﹣2）2＝0，，（b﹣2）2≥4，
∴a+1＝0，b﹣5＝0，
解得a＝﹣1，b＝4，
∴a﹣b＝﹣1﹣2＝﹣2．
故答案为：﹣3．
12．【答案】2024．
【解答】解：∵x﹣2024≥0
∴x≥2024，
∴＝x﹣2023，
∴x﹣2023+＝x，
∴＝2023，
∴x﹣2024＝20236，
∴x﹣20232＝2024．
故答案为：2024．
13．【答案】．
【解答】解：∵四边形ABCD是菱形，
∴AC、BD互相垂直平分，
∴DO＝BD＝，CO＝×4＝4，
在Rt△COD中，由勾股定理可得：
DC＝＝，
∵AE⊥DC，
∴AE×DC＝AC×DO，
∴AE＝＝，
即：CD边上的高AE＝，
故答案为：．
14．【答案】．
【解答】解：∵AB平移得到格点线段CD，
∴AB∥CD，AB＝CD，
∴△APB∽△DPC，
∴＝＝1，
即AP＝DP，
∵AD＝＝，
∴AP＝AD＝．
故答案为：．
15．【答案】1．
【解答】在Rt△ABC中，∠BAC＝90°，BC＝10，
∴AC＝＝3，
∵AD是△ABC的角平分线，
∴∠BAG＝∠FAG＝45°，
∵BG⊥AD，
∴∠AGB＝∠AGF＝90°，
在△ABG和△AFG中，
，
∴ABG≌△AFG（ASA），
∴AB＝AF＝6，BG＝FG，
∴CF＝AC＝AF＝8﹣3＝2，
∵E是斜边BC的中点，
∴EG是△BCF的中位线，
∴EG＝CF＝1．
故答案为：1．
16．【答案】90．
【解答】解：连接AC，
由正方形ABCD，AN＝BM，NO＝12，
得△ANB≌△BMC（SAS），
得BN⊥CM，
由AN＝BM，
得ND＝AM，
得△NDC的面积＝△AMC的面积，
得阴影部分的面积之和＝△MOB的面积+△AMC的面积＝△ABC的面积﹣△BOC的面积＝△NBC的面积﹣△BOC的面积＝△NOC的面积＝＝＝90．
三、（本大题共7小题，满分52分.请在答题卷的相应位置作答.）
17．【答案】．
【解答】解：
＝
＝．
18．【答案】，．
【解答】解：原式＝[+]•
＝•
＝，
当m＝﹣1时＝．
19．【答案】见试题解答内容
【解答】（1）证明：∵在△BCD中，BD＝1，BC＝，
∴BD5+CD2＝14+22＝（）2＝BC2，
∴△BCD是直角三角形，且∠CDB＝90°，
∴CD⊥AB；
（2）解：∵CD⊥AB，
∴∠ADC＝90°，
∵AB＝5，DB＝1，
∴AD＝3，
在Rt△ACD中，∵CD＝5，
∴AC＝＝＝，
∴AC的长为．
20．【答案】（1）见解答；
（2）见解答．
【解答】解：（1）正方形如图1所示
（图形位置不唯一）；
（2）三角形如图2所示．
（图形位置不唯一）．
21．【答案】（1）﹣＜﹣；
（2）+2．
【解答】解：（1）﹣＝，﹣＝，
∵+＞+＞7，
∴＜，
即﹣＜﹣；
（2）∵x+5≥0且x﹣1≥3，
∴x≥1，
∵﹣
＝
＝，
∴当x＝1时，分母+，
∴﹣的最大值为，
那么﹣+2的最大值为．
22．【答案】（1）证明见解析；
（2）．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AB∥DC且AB＝DC，
∴∠ABE＝∠DCF，
在△ABE和△DCF中，
，
∴△ABE≌△DCF（SAS），
∴AE＝DF，∠AEB＝∠DFC＝90°，
∴AE∥DF，
∴四边形ADFE是平行四边形，
∵∠DFC＝90°，
∴平行四边形ADFE是矩形；
（2）解：由（1）知：四边形ADFE是矩形，
∴EF＝AD＝3，
∵四边形ABCD是平行四边形，
∴BC＝AD＝3，CD＝AB，
∴BE＝CF＝BC﹣EC＝3，
∴BF＝BC+CF＝4，
在Rt△ABE中，∠ABE＝60°，
∴∠BAE＝90°﹣∠ABE＝30°，
∴AB＝2BE＝3，
∴DF＝AE＝＝＝，
∴BD＝＝＝，
∵∠DFB＝90°，OB＝OD，
∴OF＝BD＝．
23．【答案】（1）（2）证明见解答过程．
【解答】证明：（1）∵M是边AB的中点，
∴AM＝BM，
∵DM＝AM，
∴AM＝DM＝BM，
∴∠MAD＝∠MDA，∠MBD＝∠MDB，
∵∠MAD+∠MDA+∠MBD+∠MDB＝180°，
∴∠MDA+∠MDB＝90°，
∴AD⊥BD；
（2）∵AD⊥BD，ME⊥AD，
∴BD∥ME，
∵DE∥AB，
∴四边形EMBD为平行四边形，
∴DE＝BM＝AM，
∴四边形AEDM为平行四边形，
∵DM＝AM，
∴平行四边形AEDM是菱形．