初中人教版13.4课题学习 最短路径问题课文配套ppt课件

这是一份初中人教版13.4课题学习 最短路径问题课文配套ppt课件，共24页。PPT课件主要包含了学习目标，复习导入，点C应该在哪里，两点之间线段最短，练一练，课堂练习等内容，欢迎下载使用。
能利用轴对称变换解决实际问题
能利用作图解决生活中的轴对称问题（作图建模）
问题：如何画出点A关于直线l的对称点A′.
作法：（1）过点 A 作 l 的垂线，垂足为点 O.（2）在垂线上截取 OA′=OA 点 A′ 就是点 A关于直线 l 的对称点.
对称轴是对称点所连的线段的垂直平分线.
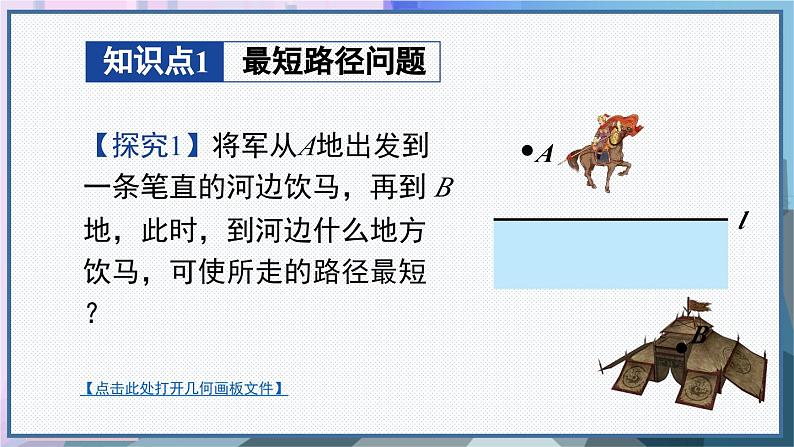
【探究1】将军从A地出发到一条笔直的河边饮马，再到 B 地，此时，到河边什么地方饮马，可使所走的路径最短？
【点击此处打开几何画板文件】
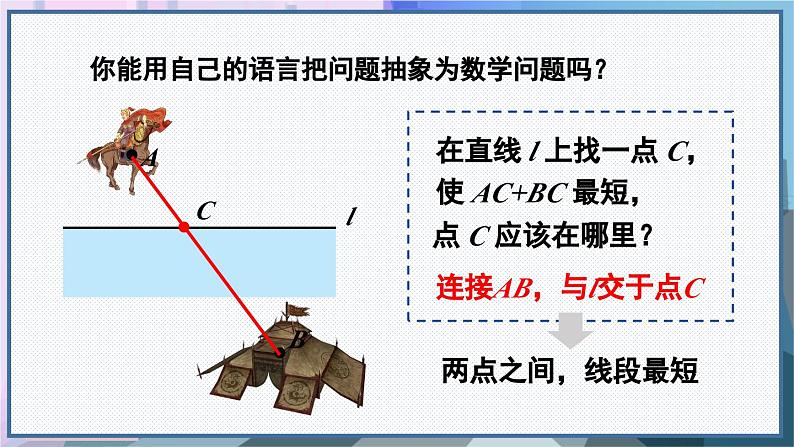
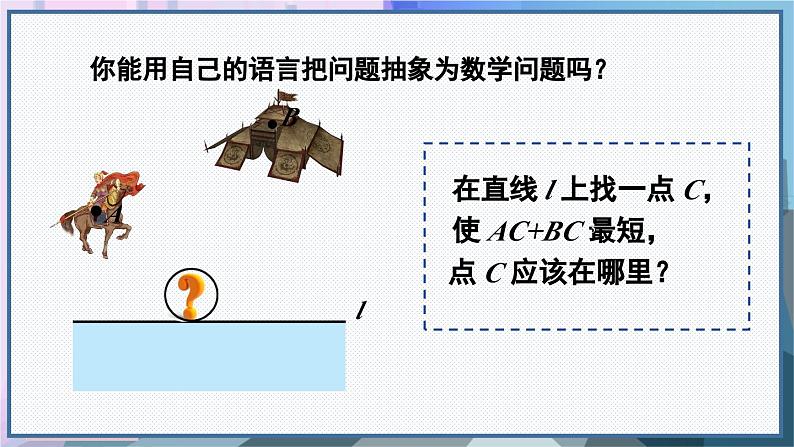
你能用自己的语言把问题抽象为数学问题吗？
在直线 l 上找一点 C，使 AC+BC 最短，
连接AB，与l交于点C
【探究2】将军出发的地方 A和军营 B 在河的同一边，此时，到河边什么地方饮马，可使所走的路径最短？
（1）这两个问题之间，有什么相同点和不同点？（2）我们能否把右图A、B两点转化到直线l的异侧呢？
①找到点 A 关于直线l的对称点 A′；
②连接 A′B，与直线l的交点就是所求点 C.
AC+BC 就是将军走的最短路程
你能证明 AC+BC 最短吗？
证明：如图，在直线l 上任取一点C′（与点C 不重合）连接 AC′，BC′，A′C′．由轴对称的性质知，AC =A′C，AC′=A′C′．∴AC +BC= A′C +BC = A′B，AC′+BC′ = A′C′+BC′．
在△A′BC′中，A′B＜A′C′+BC′，∴AC +BC＜AC′+BC′．即 AC +BC 最短．
如图，A，B 是两个居民小区，快递公司准备在公路上选取一点 P 建一个服务中心，使 PA+PB 最短.下面四种选址方案符合要求的是（ ）
如图所示，A 和 B 两地在一条河的两岸，现要在河上造一座桥MN，桥造在何处可使从 A 到 B 的路径AMNB最短？（假定河的两岸是平行的直线，桥要与河垂直.）
当点N在直线b的什么位置时，AM+MN+BN最小
当点N在直线b的什么位置时，AM+BN最小
将 AM 沿与河岸垂直的方向平移，点 M 移动到点 N，点 A 移动到点 A′，则 AA′=MN，AM+NB=A′N+NB.
当点 N 在直线 b 的什么位置时 A′N+NB 最小
在连接 A′，B 两点的线中，线段 A′B 最短.因此，线段A′B 与直线 b 的交点 N 的位置即为所求，即在点 N 出造桥 MN，所得路径 AMNB 是最短的.
证明：如图，在直线 b 上任取一点 N′,过点 N′ 作N′M′⊥a，垂足为 M′，连接AM′ , A′N′ , N′B .由平移的性质知，AM =A′N，AM′=A′N′，MN=M′N′∴AM +NB= A′N +NB = A′B， AM′+BN′ = A′N′+BN′．
在△A′BN′中，A′B＜A′N′+BN′，∴AM +MN +NB＜AM′+M′N′+BN′．即 AM +MN +NB 最短．
有一条以互相平行的直线 a，b 为岸的河流，其两侧有村庄 A 和村庄 B.现在要在河上建一座桥梁 MN (桥与河岸垂直).使两村庄之间往来的路径最短，从作图痕迹上来看，正确的是（ ）
1.作图在直线 l 上找一点C，使 AC+BC 最小.
2.如图，已知牧马营地在P处，每天牧马人要赶着马群先到河边饮水，再带到草地吃草，请你替牧马人设计出最短的放牧路线.
解：如图 AP+AB 即为最短的放牧路线.
解：如图，作点 M 关于BC的对称点 M′，连接 M′N，交 BC 于点 P，则△PMN的周长最小.
3.如图，M、N分别是 △ABC 的边 AB、AC 上的点，在边 BC 上求作一点 P，使 △PMN 的周长最小.
4.如图，已知直线 MN 与 MN 异侧两点 A、B，在MN 上求作一点 P，使 PA－PB 最大，请说明理由.
解：如图，作B点关于 MN 的对称点 B′，连接 AB′并延长，交 MN 于点 P，点 P 即为所求. 理由：点 A，B′，P 在同一条直线上时，PA－PB′ 最大，即PA－PB 最大.
在解决最短路径问题时，我们通常利用轴对称、平移等变化把已知问题转化为容易解决的问题，从而作出最短路径的选择.