

所属成套资源:浙教版八年级数学下册专题特训(原卷版+解析)
浙教版八年级数学下册专题1.1二次根式(知识解读)(原卷版+解析)
展开
这是一份浙教版八年级数学下册专题1.1二次根式(知识解读)(原卷版+解析),共15页。
了解二次根式的概念
理解二次根式有意义的条件,会求二次根式的被开方数中所含字母的取值范围。
掌握二次根式的性质,能利用二次根式的性质进行化简
【知识点梳理】
知识点1:二次根式
二次根式的概念
一般地,我们把形如 的式子的式子叫做二次根式,称为 称为二次根号.
二次根式满足条件:
必须含有二次根号
被开方数必须是非负数
如都是二次根式。
知识点2:二次根式有无意义的条件
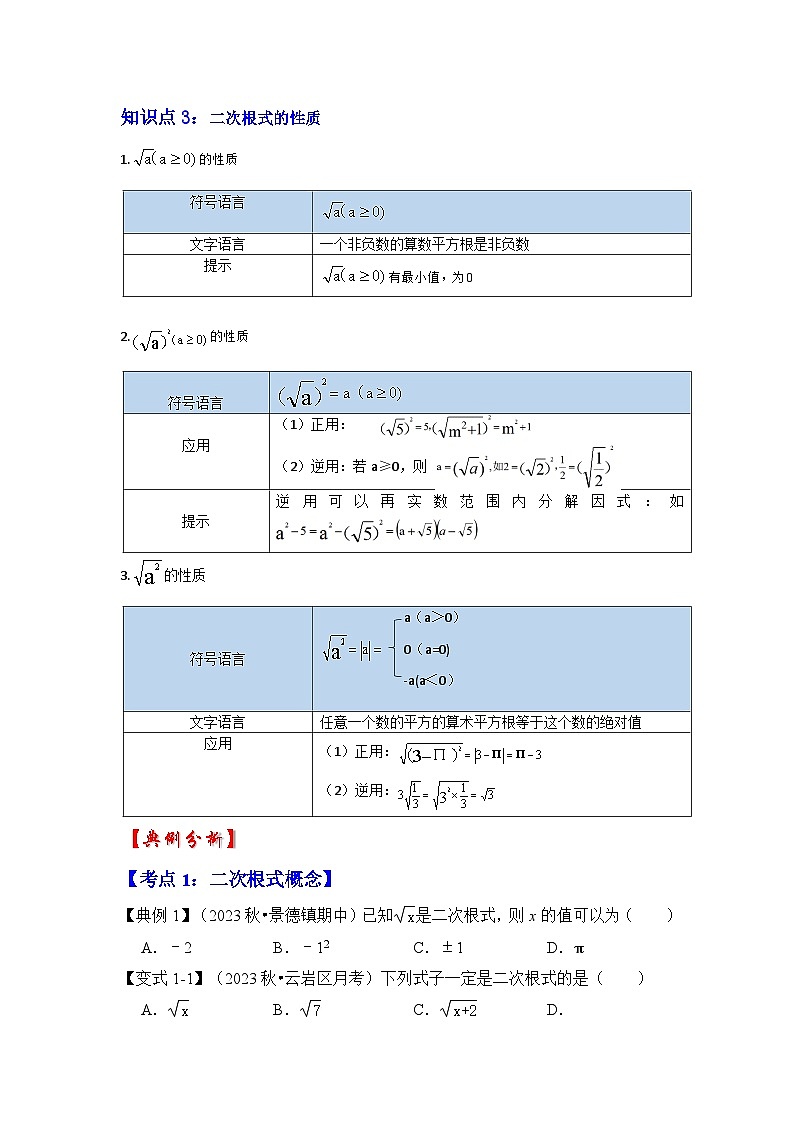
知识点3:二次根式的性质
1.的性质
2.的性质
3.的性质
【典例分析】
【考点1:二次根式概念】
【典例1】(2023秋•景德镇期中)已知是二次根式,则x的值可以为( )
A.﹣2B.﹣12C.±1D.π
【变式1-1】(2023秋•云岩区月考)下列式子一定是二次根式的是( )
A.B.C.D.
【变式1-2】(2023秋•新蔡县校级月考)下列各式中,一定是二次根式的是( )
A.B.C.D.
【变式1-3】(2023春•宜城市期末)在式子,,,x+y中,二次根式有( )
A.1个B.2个C.3个D.4个
【典例2】(2023春•昭阳区校级月考)若是整数,则正整数n的最小值是( )
A.2B.3C.4D.5
【变式2-1】(2023春•朝阳区期末)若是整数,则正整数n的最小值是( )
A.3B.7C.9D.63
【变式2-2】(2023•南京模拟)若是整数,则a能取的最小整数为( )
A.0B.1C.2D.3
【考点2:二次根式有无意义的条件】
【典例3】(2023秋•潮南区期末)若式子在实数范围内有意义,则a的取值范围是( )
A.a≥﹣1B.a≠2C.a≥﹣1且a≠2D.a>2
【变式3-1】(2023•大理州二模)若二次根式有意义,则x的取值范围是( )
A.x≥0B.x≥5C.x≥﹣5D.x≤5
【变式3-2】(2023秋•宁安市期末)若代数式在实数范围内有意义,则x的取值范围为( )
A.x≥0且x≠2B.x≥0C.x≠0D.x>0且x≠2
【考点3:二次根式性质】
【典例3-1】(2023春•广陵区期末)化简二次根式﹣的结果为( )
A.2aB.﹣2C.2aD.﹣2a
【典例3-2】(2023春•兰山区期末)下列计算正确的是( )
A.B.C.D.
【变式3-1】(2023春•无棣县期末)下列等式正确的是( )
A.=﹣2B.=±9C.=﹣2D.=﹣5
【变式3-2】(2023春•新市区校级期末)下列各式中,正确的是( )
A.B.﹣C.D.
【变式3-3】(2023•山海关区一模)实数a,b在数轴上对应的位置如图所示,化简的结果是( )
A.2b﹣aB.a+2bC.﹣aD.a
【典例4】(2023春•冠县期末)当x>2时,=( )
A.2﹣xB.x﹣2C.2+xD.±(x﹣2)
【变式4】(2023秋•石鼓区期末)若a<0,则化简|a﹣3|﹣的结果为( )
A.3﹣2aB.3C.﹣3D.2a﹣3
【典例5】(2023春•德城区校级期中)若=3﹣x成立,则x满足得条件( )
A.x≥3B.x≤3C.x>3D.x<3
【变式5-1】(2023•南京模拟)若成立,则x满足的条件是( )
A.x>2B.x<﹣2C.x≥﹣2D.x≤﹣2
【变式5-2】(2023春•广阳区校级期末)当1<a<2时,代数式+的值是( )
A.1B.﹣1C.2a﹣3D.3﹣2a
【变式5-3】(2023春•秭归县期中)若1≤x≤4,化简|1﹣x|﹣的结果为( )
A.3B.2x﹣5C.﹣3D.5﹣2x
【典例6】(2023春•宜秀区校级月考)已知|2020﹣a|+=a,则4a﹣40402的值为( )
A.8084B.6063C.4042D.2021
【变式6-1】(2023•南京模拟)已知,则(x+y)2000(x﹣y)2001的值为( )
A.B.C.﹣1D.1
【变式6-2】(2023秋•南湖区校级期中)已知y=++4,yx的平方根是( )
A.16B.8C.±4D.±2
条件
字母表示
二次根式有意义
被开方数为非负数
二次根式无意义
被开方数为负数
符号语言
文字语言
一个非负数的算数平方根是非负数
提示
有最小值,为0
符号语言
应用
正用:
逆用:若a≥0,则
提示
逆用可以再实数范围内分解因式:如
符号语言
a(a>0)
0(a=0)
-a(a<0)
文字语言
任意一个数的平方的算术平方根等于这个数的绝对值
应用
正用:
逆用:
专题1.1 二次根式(知识解读)
【学习目标】
了解二次根式的概念
理解二次根式有意义的条件,会求二次根式的被开方数中所含字母的取值范围。
掌握二次根式的性质,能利用二次根式的性质进行化简
【知识点梳理】
知识点1:二次根式
二次根式的概念
一般地,我们把形如 的式子的式子叫做二次根式,称为 称为二次根号.
二次根式满足条件:
必须含有二次根号
被开方数必须是非负数
如都是二次根式。
知识点2:二次根式有无意义的条件
知识点3:二次根式的性质
1.的性质
2.的性质
3.的性质
【典例分析】
【考点1:二次根式概念】
【典例1】(2023秋•景德镇期中)已知是二次根式,则x的值可以为( )
A.﹣2B.﹣12C.±1D.π
答案:D
【解答】解:∵x≥0,
∴x的值可以为π,
故选:D.
【变式1-1】(2023秋•云岩区月考)下列式子一定是二次根式的是( )
A.B.C.D.
答案:B
【解答】解:A、当x<0时,二次根式无意义,故选项A一定是二次根式,选项A不符合题意;
B、是二次根式,故选项B符合题意;
C、当x+2<0时,此时二次根式无意义,故选项C不一定是二次根式,选项C不符合题意;
D、﹣2<0,二次根式无意义,故选项D一定不是二次根式,选项D不符合题意;
故选:B.
【变式1-2】(2023秋•新蔡县校级月考)下列各式中,一定是二次根式的是( )
A.B.C.D.
答案:B
【解答】解:A.当a<0时,无意义,故此选项不合题意;
B.是二次根式,故此选项符合题意;
C.是三次根式,故此选项不合题意;
D.的被开方数是负数,该式子无意义,故此选项不合题意;
故选:B.
【变式1-3】(2023春•宜城市期末)在式子,,,x+y中,二次根式有( )
A.1个B.2个C.3个D.4个
答案:B
【解答】解:在式子,,,x+y中,二次根式有,,
共有2个,
故选:B.
【典例2】(2023春•昭阳区校级月考)若是整数,则正整数n的最小值是( )
A.2B.3C.4D.5
答案:D
【解答】解:∵=4,
∴正整数n的最小值是:5.
故选:D.
【变式2-1】(2023春•朝阳区期末)若是整数,则正整数n的最小值是( )
A.3B.7C.9D.63
答案:B
【解答】解:∵=3,,且是整数;
∴3是整数,即7n是完全平方数;
∴n的最小正整数值为7.
故选:B.
【变式2-2】(2023•南京模拟)若是整数,则a能取的最小整数为( )
A.0B.1C.2D.3
答案:A
【解答】解:∵成立,
∴4a+1≥0,
解得,
又∵是整数,
∴a能取的最小整数为0,
故选:A.
【考点2:二次根式有无意义的条件】
【典例3】(2023秋•潮南区期末)若式子在实数范围内有意义,则a的取值范围是( )
A.a≥﹣1B.a≠2C.a≥﹣1且a≠2D.a>2
答案:C
【解答】解:根据题意,得a+1≥0且a﹣2≠0.
解得a≥﹣1且a≠2.
故选:A.故选:C.
【变式3-1】(2023•大理州二模)若二次根式有意义,则x的取值范围是( )
A.x≥0B.x≥5C.x≥﹣5D.x≤5
答案:B
【解答】解:∵x﹣5≥0,
∴x≥5.
故选:B.
【变式3-2】(2023秋•宁安市期末)若代数式在实数范围内有意义,则x的取值范围为( )
A.x≥0且x≠2B.x≥0C.x≠0D.x>0且x≠2
答案:A
【解答】解:由题意得:3x≥0且x﹣2≠0,
解得:x≥0且x≠2
【考点3:二次根式性质】
【典例3-1】(2023春•广陵区期末)化简二次根式﹣的结果为( )
A.2aB.﹣2C.2aD.﹣2a
答案:D
【解答】解:∵8a3≥0,
∴a≥0
∴﹣=﹣=﹣2a,
故选:D.
【典例3-2】(2023春•兰山区期末)下列计算正确的是( )
A.B.C.D.
答案:D
【解答】解:因为:=|a|,
所以:=2,=2,
故选:D.
【变式3-1】(2023春•无棣县期末)下列等式正确的是( )
A.=﹣2B.=±9C.=﹣2D.=﹣5
答案:C
【解答】解:CA、=2,故A不符合题意;
B、=9,故B不符合题意;
C、=﹣2,故C符合题意;
D、无意义,故D不符合题意;
故选:C.
【变式3-2】(2023春•新市区校级期末)下列各式中,正确的是( )
A.B.﹣C.D.
答案:B
【解答】解:∵=|﹣3|=3,
∴A选项的结论不正确;
∵﹣=﹣3,
∴B选项的结论正确;
∵=|﹣3|=3,
∴C选项的结论不正确;
∵=3,
∴D选项的结论不正确,
故选:B.
【变式3-3】(2023•山海关区一模)实数a,b在数轴上对应的位置如图所示,化简的结果是( )
A.2b﹣aB.a+2bC.﹣aD.a
答案:B
【解答】解:由数轴可知:b<0<a,|a|>|b|,
∴a+b>0,
∴原式=(a+b)﹣(﹣b)
=b+a+b
=a+2b,
故选:B.
【典例4】(2023春•冠县期末)当x>2时,=( )
A.2﹣xB.x﹣2C.2+xD.±(x﹣2)
答案:B
【解答】解:由题意可知:2﹣x<0,
∴原式=|2﹣x|
=﹣(2﹣x)
=﹣2+x,
故选:B.
【变式4】(2023秋•石鼓区期末)若a<0,则化简|a﹣3|﹣的结果为( )
A.3﹣2aB.3C.﹣3D.2a﹣3
答案:B
【解答】解:∵a<0,
∴a﹣3<0,
∴|a﹣3|﹣
=3﹣a﹣(﹣a)
=3﹣a+a
=3,
故选:B.
【典例5】(2023春•德城区校级期中)若=3﹣x成立,则x满足得条件( )
A.x≥3B.x≤3C.x>3D.x<3
答案:B
【解答】解:∵=|3﹣x|=3﹣x,
∴3﹣x≥0,解得x≤3.
故选:B.
【变式5-1】(2023•南京模拟)若成立,则x满足的条件是( )
A.x>2B.x<﹣2C.x≥﹣2D.x≤﹣2
答案:D
【解答】解:∵,
∴2+x≤0,
解得x≤﹣2,
故选:D.
【变式5-2】(2023春•广阳区校级期末)当1<a<2时,代数式+的值是( )
A.1B.﹣1C.2a﹣3D.3﹣2a
答案:A
【解答】解:∵1<a<2,
∴a﹣2<0,a﹣1>0,
∴原式=|a﹣2|+|a﹣1|
=2﹣a+a﹣1
=1.
故选:A.
【变式5-3】(2023春•秭归县期中)若1≤x≤4,化简|1﹣x|﹣的结果为( )
A.3B.2x﹣5C.﹣3D.5﹣2x
答案:B
【解答】解:∵1≤x≤4,
∴|1﹣x|﹣
=x﹣1﹣(4﹣x)
=2x﹣5.
故选:B
【典例6】(2023春•宜秀区校级月考)已知|2020﹣a|+=a,则4a﹣40402的值为( )
A.8084B.6063C.4042D.2021
答案:A
【解答】解:由题意得,a﹣2021≥0,
解得,a≥2021,
原式变形为:a﹣2020+=a,
则=2020,
∴a﹣2021=20202,
∴4a=4×20202+8084,
∴4a﹣40402=40402+8084﹣40402=8084,
故选:A.
【变式6-1】(2023•南京模拟)已知,则(x+y)2000(x﹣y)2001的值为( )
A.B.C.﹣1D.1
答案:B
【解答】解:∵,
∴x=2,y=﹣,
则(x+y)2000(x﹣y)2001=(2﹣)2000×(2+)2001
=[(2+)×(2﹣)]2000×(2+)
=(4﹣3)2000×(2+)
=1×(2+)
=2+.
故选:B.
【变式6-2】(2023秋•南湖区校级期中)已知y=++4,yx的平方根是( )
A.16B.8C.±4D.±2
答案:C
【解答】解:∵y=++4,
∴,
解得x=2,
∴y=4,
∴yx=42=16.
∴yx的平方根是±4.
故选:C.
条件
字母表示
二次根式有意义
被开方数为非负数
二次根式无意义
被开方数为负数
符号语言
文字语言
一个非负数的算数平方根是非负数
提示
有最小值,为0
符号语言
应用
正用:
逆用:若a≥0,则
提示
逆用可以再实数范围内分解因式:如
符号语言
a(a>0)
0(a=0)
-a(a<0)
文字语言
任意一个数的平方的算术平方根等于这个数的绝对值
应用
正用:
逆用:
相关试卷
这是一份初中数学浙教版八年级下册1.1 二次根式精练,共20页。
这是一份初中数学1.1 二次根式课后测评,共17页。
这是一份初中数学浙教版八年级下册1.1 二次根式当堂检测题,共10页。









