2024年中考数学二轮复习 压轴题 专项培优练习01（含答案）

这是一份2024年中考数学二轮复习 压轴题 专项培优练习01（含答案），共15页。试卷主要包含了B，交y轴于C．等内容，欢迎下载使用。

如图，抛物线与x轴交于A(﹣1，0)、B(3，0)，交y轴于C(0，3)．
(1)求抛物线的解析式；
(2)P是直线BC上方的抛物线上的一个动点，设P的横坐标为t，P到BC的距离为h，求h与t的函数关系式，并求出h的最大值；
(3)设点M是x轴上的动点，在平面直角坐标系中，存在点N，使得以点A、C、M、N为顶点的四边形是菱形，直接写出所有符合条件的点N坐标．
如图，在平面直角坐标系中，抛物线y＝﹣eq \f(1,2)x2＋bx＋eq \f(3,2)与x轴正半轴交于点A，且点A的坐标为(3，0)，过点A作垂直于x轴的直线l，P是该抛物线上一动点，其横坐标为m，过点P作PQ⊥l于点Q，M是直线l上的一点，其纵坐标为﹣m＋eq \f(3,2)．以PQ，QM为边作矩形PQMN．
(1)求抛物线的解析式；
(2)当点Q与点M重合时，求m的值；
(3)当矩形PQMN是正方形，且抛物线的顶点在该正方形内部时，求m的值；
(4)当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小时，求m的取值范围．
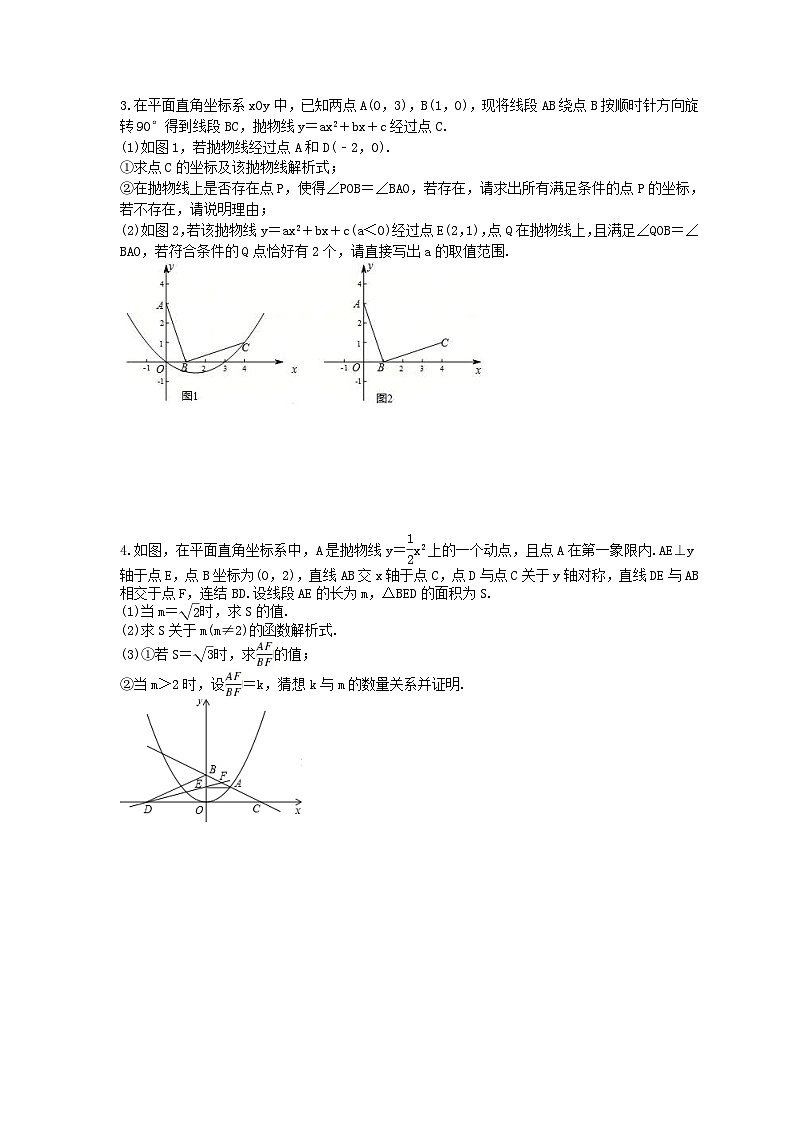
在平面直角坐标系xOy中，已知两点A(0，3)，B(1，0)，现将线段AB绕点B按顺时针方向旋转90°得到线段BC，抛物线y＝ax2＋bx＋c经过点C.
(1)如图1，若抛物线经过点A和D(﹣2，0).
①求点C的坐标及该抛物线解析式；
②在抛物线上是否存在点P，使得∠POB＝∠BAO，若存在，请求出所有满足条件的点P的坐标，若不存在，请说明理由；
(2)如图2，若该抛物线y＝ax2＋bx＋c(a＜0)经过点E(2，1)，点Q在抛物线上，且满足∠QOB＝∠BAO，若符合条件的Q点恰好有2个，请直接写出a的取值范围.
如图，在平面直角坐标系中，A是抛物线y＝eq \f(1,2)x2上的一个动点，且点A在第一象限内.AE⊥y轴于点E，点B坐标为(0，2)，直线AB交x轴于点C，点D与点C关于y轴对称，直线DE与AB相交于点F，连结BD.设线段AE的长为m，△BED的面积为S.
(1)当m＝eq \r(2)时，求S的值.
(2)求S关于m(m≠2)的函数解析式.
(3)①若S＝eq \r(3)时，求的值；
②当m＞2时，设＝k，猜想k与m的数量关系并证明.
如图(1)，△ABC中，AC＝BC＝6，∠C＝90°，点P在线段AC上，从C点向A点运动，∠PBE＝90°，BP＝BE，PE交BC于点D，完成下列问题：
(1)①点E到BC边的距离为 ；
②若CD＝x，△BDE的面积为S，则S与x的函数关系式为 ；(不写自变量取值范围)
(2)当△BDE的面积为15时，若PC＜eq \f(1,2)AC，以C为原点，AC、BC所在直线分别为x、y轴建立坐标系如图(2)，抛物线C1过点A、D、B；
①点Q在抛物线C1上，且位于线段PB的下方，过点Q作QN⊥PB，垂足为点N，是否存在点Q，使得QN最长，若存在，请求出QN的长度和Q点坐标；若不存在，请说明理由；
②将抛物线C1绕原点C旋转180°，得到抛物线C2，当﹣2a≤x≤﹣a时(a＞0)，抛物线C2有最大值2a，求a值．
如图，已知二次函数y=ax2＋bx＋c(a≠0)图象经过点A(1，0)，B(2，0)，C(0，﹣2)，直线x=m(m＞2)与x轴交于点D．
(1)求二次函数的解析式；
(2)在直线x=m(m＞2)上有一点E(点E在第四象限)，使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似，求E点坐标(用含m的代数式表示)；
(3)在(2)成立的条件下，抛物线上是否存在一点F，使得四边形ABEF为平行四边形？若存在，请求出F点的坐标；若不存在，请说明理由．
如图，抛物线y＝ax2＋bx＋c与x轴交于A(3，0)、B(﹣1，0)两点，与y轴交于点C(0，3)，其顶点为点D，连结AC．
(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标；
(2)在抛物线的对称轴上取一点E，点F为抛物线上一动点，使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形，求点F的坐标；
(3)在(2)的条件下，将点D向下平移5个单位得到点M，点P为抛物线的对称轴上一动点，求PF＋eq \f(3,5)PM的最小值．
如图1，抛物线y＝x2＋(m﹣2)x﹣2m(m＞0)与x轴交于A，B两点(A在B左边)，与y轴交于点C．连接AC，BC．且△ABC的面积为8．
(1)求m的值；
(2)在(1)的条件下，在第一象限内抛物线上有一点T，T的横坐标为t，使∠ATC＝60°．求(t﹣1)2的值．
(3)如图2，点P为y轴上一个动点，连接AP，求CP＋eq \r(5)AP的最小值，并求出此时点P的坐标．
\s 0 答案
解：(1)∵抛物线y＝ax2＋bx＋c过A(﹣1，0)、B(3，0)、C(0，3)三点，
∴，解得 ，
∴抛物线的解析式为y＝﹣x2＋2x＋3；
(2)如图1，过点P作PD⊥x轴于点D，交BC于点E，PH⊥BC于点H，连接PB、PC，‘
∵B(3，0)、C(0，3)，
∴OB＝OC＝3，BC＝3eq \r(2)，
设直线BC解析式为y＝kx＋n，
则，解得 ，
∴直线BC解析式为y＝﹣x＋3，
∵点P的横坐标为t，且在抛物线y＝﹣x2＋2x＋3上，
∴P(t，﹣t2＋2t＋3)，
又∵PD⊥x轴于点D，交BC于点E，
∴D(t，0)，E(t，﹣t＋3)，
∴PE＝(﹣t2＋2t＋3)﹣(﹣t＋3)＝﹣t2＋3t，
∴S△PBC＝eq \f(1,2)PE( xB﹣xC )＝eq \f(1,2)(﹣t2＋3t)×3＝﹣eq \f(3,2)t2＋eq \f(9,2)t，
又∵S△PBC＝eq \f(1,2)BCPH＝eq \f(1,2)×3 eq \r(2)h＝eq \f(3\r(2),2)h，
∴eq \f(3\r(2),2)h＝﹣eq \f(3,2)t2＋eq \f(9,2)t，
∴h与t的函数关系式为：h＝﹣eq \f(\r(2),2)t2＋eq \f(3\r(2),2)t(0＜t＜3)，
∵，
∴当t＝eq \f(3,2)时，h有最大值为eq \f(9,8)eq \r(2)；
(3)存在．①若AM为菱形对角线，如图2，
则AM与CN互相垂直平分，∴N(0，﹣3)；
②若CM为菱形对角线，如图3和图4，
则CN＝AM＝AC＝，∴N(﹣，3)或N(，3)；
③若AC为菱形对角线，如图5，
则CN＝AM＝CM，设M(m，0)，
由CM2＝AM2，得m2＋32＝(m＋1)2，解得m＝4，
∴CN＝AM＝CM＝5，
∴N(﹣5，3)．
综上可知存在点N，使得以点A、C、M、N为顶点的四边形是菱形，符合条件的点N有4个：(0，﹣3)或(﹣eq \r(10)，3)或(eq \r(10)，3)或(﹣5，3)．
解：(1)当x＝2时，y＝﹣eq \f(3,2)．
∴点B的坐标为(2，﹣eq \f(3,2))，
当y＝0时，eq \f(1,2)x2﹣x﹣eq \f(3,2)＝0．解得x1＝﹣1，x2＝3．
∵抛物线y＝eq \f(1,2)x2﹣x﹣eq \f(3,2)与x轴正半轴交于点A，
∴点A的坐标为(3，0)．
由题意，得，解得，
∴直线AB对应的函数关系式为y＝eq \f(3,2)x﹣eq \f(9,2)．
(2)当点P与点A重合时，m＋1＝3．解得m＝2．
∴2m＝4．
∵点D的纵坐标为1．
∴点E的坐标为(4，1)．
(3)将y＝eq \f(1,2)x2﹣x﹣eq \f(3,2)配方，得y＝eq \f(1,2)(x﹣1)2﹣2．
∴抛物线的顶点坐标为(1，﹣2)．
由题意，得点E的坐标为(2m,eq \f(1,2)m2﹣1)．
∵点E在该抛物线上，
∴．解得，．
当2m＜1时，即m∵，
∴抛物线的顶点到EF的距离为．
当2m＞1时，即m>eq \f(1,2)，顶点(1，﹣2)在EF的左边．
∵，
∴抛物线的顶点到EF的距离为．
综上所述，抛物线的顶点到EF的距离为或．
(4)当点F(2m，eq \f(3,2)m﹣3)在抛物线上时，eq \f(3,2)m﹣3＝2m2﹣2m﹣eq \f(3,2)，解得m＝eq \f(3,4)或1，
当E在抛物线上时，m＝，当点P与A重合时，m＝2，
观察图1，图2，图3可知，当或或
m≥2时，矩形CDEF的一组邻边与该抛物线相交．
也可以写成：当或m≠1或m≥2时，矩形CDEF的一组邻边与该抛物线相交．
解：(1)①如图2，∵A(0，3)，B(1，0)，
∴OA＝3，OB＝1，
由旋转知，∠ABC＝90°，AB＝CB，
∴∠ABO＋∠CBE＝90°，
过点C作CG⊥OB于G，
∴∠CBG＋∠BCG＝90°，
∴∠ABO＝∠BCG，
∴△AOB≌△GBC，
∴CG＝OB＝1，BG＝OA＝3，
∴OG＝OB＋BG＝4
∴C(4，1)，
抛物线经过点A(0，3)，和D(﹣2，0)，
∴∴，
∴抛物线解析式为y＝﹣eq \f(1,3)x2＋eq \f(5,6)x＋3；
②由①知，△AOB≌△EBC，
∴∠BAO＝∠CBF，
∵∠POB＝∠BAO，
∴∠POB＝∠CBF，
如图1，OP∥BC，
∵B(1，0)，C(4，1)，
∴直线BC的解析式为y＝eq \f(1,3)x﹣eq \f(1,3)，
∴直线OP的解析式为y＝eq \f(1,3)x，
∵抛物线解析式为y＝﹣eq \f(1,3)x2＋eq \f(5,6)x＋3；
联立解得，或(舍)
∴P(，)；
在直线OP上取一点M(3，1)，∴点M的对称点M'(3，﹣1)，
∴直线OP'的解析式为y＝﹣eq \f(1,3)x，
∵抛物线解析式为y＝﹣eq \f(1,3)x2＋eq \f(5,6)x＋3；
联立解得，或(舍)，
∴P'(，﹣)；
(2)同(1)②的方法，如图3，
∵抛物线y＝ax2＋bx＋c经过点C(4，1)，E(2，1)，
∴，∴，
∴抛物线y＝ax2﹣6ax＋8a＋1，
令y＝0，∴ax2﹣6ax＋8a＋1＝0，
∴x1×x2＝
∵符合条件的Q点恰好有2个，
∴方程ax2﹣6ax＋8a＋1＝0有一个正根和一个负根或一个正根和0，
∴x1×x2＝≤0，
∵a＜0，∴8a＋1≥0，∴a≥﹣eq \f(1,8)，
即：﹣eq \f(1,8)≤a＜0.
解：(1)∵点A在二次函数y＝eq \f(1,2)x2的图象上，AE⊥y轴于点E，且AE＝m，
∴点A的坐标为(m，eq \f(1,2) m2)，
当m＝eq \r(2)时，点A的坐标为(eq \r(2)，1)，
∵点B的坐标为(0，2)，
∴BE＝OE＝1.
∵AE⊥y轴，
∴AE∥x轴，
∴△ABE∽△CBO，
∴＝＝，
∴CO＝2eq \r(2)，
∵点D和点C关于y轴对称，
∴DO＝CO＝2eq \r(2)，
∴S＝eq \f(1,2)BE•DO＝eq \f(1,2)×1×2eq \r(2)＝eq \r(2)；
(2)(I)当0＜m＜2时(如图1)，
∵点D和点C关于y轴对称，
∴△BOD≌△BOC，
∵△BEA∽△BOC，
∴△BEA∽△BOD，
∴＝，即BE•DO＝AE•BO＝2m.
∴S＝eq \f(1,2)BE•DO＝eq \f(1,2)×2m＝m；
(II)当m＞2时(如图2)，
同(I)解法得：S＝eq \f(1,2)BE•DO＝eq \f(1,2)AE•OB＝m，
由(I)(II)得，S关于m的函数解析式为S＝m(m＞0且m≠2).
(3)①如图3，连接AD，
∵△BED的面积为eq \r(3)，
∴S＝m＝eq \r(3)，
∴点A的坐标为(eq \r(3)，eq \f(3,2))，
∵＝＝＝k，
∴S△ADF＝k•S△BDF，S△AEF＝k•S△BEF，
∴＝＝＝k，
∴k＝＝；
②k与m之间的数量关系为k＝eq \f(1,4)m2，
如图4，连接AD，
∵＝＝＝k，
∴S△ADF＝k•S△BDF，S△AEF＝k•S△BEF，
∴＝＝＝k，
∵点A的坐标为(m，eq \f(1,2)m2)，S＝m，
∴k＝＝m2(m＞2).
解：(1)①过点E作EH⊥BC于点H，如图，
∵∠PBE＝90°，
∴∠PBC＋∠CBE＝90°，
∵∠ACB＝90°，
∴∠CPB＋∠PBC＝90°，
∴∠CPB＝∠CBE，
在△PCB 和△BHE中，
，
∴△PCB≌△BHE(AAS)，
∴EH＝CB＝6，
∴点E到BC边的距离为6，
故答案为：6；
②∵CD＝x，BD＝6﹣x，
∴S△BDE＝eq \f(1,2)BD×EH＝eq \f(1,2)×(6﹣x)×6＝18﹣3x，
故答案为：S＝18﹣3x；
(2)①由题知点A(0，6)，点B(6，0)，
∵S△BDE＝18﹣3x＝15，
∴x＝1，
∴点D的坐标是(1，0)，
设抛物线C1：y＝ax2＋bx＋c，
将点A、D、B的坐标分别代入得，
，解得：，
∴抛物线C1的解析式为：y＝x2﹣7x＋6，
当Q与E重合，点E在抛物线上时，QN＝BE取最大值，
∵EH＝6，
∴将y＝﹣6代入抛物线得：﹣6＝x2﹣7x＋6，
解得：x1＝3，x₂＝4，
当x＝3时，BH＝6﹣3＝3＝PC，与题干PC＜eq \f(1,2)AC相矛盾，故x＝3舍去，
∴BH＝6﹣4＝2，
∴QN＝2eq \r(10)，
∴Q点的坐标为(4，﹣6)，
∴QN的最大值为2eq \r(10)，故QN的长度为2eq \r(10)，Q点的坐标是(4，﹣6)；
②将抛物线C1绕原点C旋转180°，得到抛物线C2为y＝﹣x2﹣7x﹣6，
∵y＝﹣x2﹣7x﹣6＝﹣(x＋eq \f(7,2))2＋eq \f(25,4)，
∴抛物线C2的项点坐标为(﹣eq \f(7,2)，eq \f(25,4))，
当﹣2a≤﹣eq \f(7,2)≤﹣a时，2a＝eq \f(25,4)，解得：a＝，
当﹣a＜﹣eq \f(7,2)时，即﹣2a≤x≤﹣a，在抛物线对称轴左侧，y随x的增大而增大，
∴当x＝﹣a时，取最大值，即﹣a2＋7a﹣6＝2a，
解得a1＝2，a2＝3均不在﹣a＜﹣eq \f(7,2)范围内，故均舍去，
当﹣2a＞﹣eq \f(7,2)时，即﹣2a≤x≤a，在抛物线对称轴右侧，y随x的增大而减小，
∴当x＝﹣2a 时，取最大值，
即﹣4a2＋14a﹣6＝2a，解得a＝，
∵﹣2a＞﹣eq \f(7,2)，即0，∴a＝舍去，
∴a＝，∴a＝或a＝．
解：(1)将点A(1，0)，B(2，0)，C(0，﹣2)代入二次函数y=ax2＋bx＋c中，
得 解得a=﹣1，b=3，c=﹣2．
∴y=﹣x2＋3x﹣2．
(2)∵AO=1，CO=2，BD=m﹣2，
当△EDB∽△AOC时，
得=，即=，解得ED=，
∵点E在第四象限，∴E1(m，)，
当△BDE∽△AOC时， =时，即=，解得ED=2m﹣4，
∵点E在第四象限，∴E2(m，4﹣2m)；
(3)假设抛物线上存在一点F，使得四边形ABEF为平行四边形，
则EF=AB=1，点F的横坐标为m﹣1，
当点E1的坐标为(m，)时，点F1的坐标为(m﹣1，)，
∵点F1在抛物线的图象上，∴=﹣(m﹣1)2＋3(m﹣1)﹣2，∴2m2﹣11m＋14=0，
∴(2m﹣7)(m﹣2)=0，∴m=eq \f(7,2)，m=2(舍去)，∴F1(eq \f(5,2)，﹣eq \f(3,4))，
当点E2的坐标为(m，4﹣2m)时，点F2的坐标为(m﹣1，4﹣2m)，
∵点F2在抛物线的图象上，
∴4﹣2m=﹣(m﹣1)2＋3(m﹣1)﹣2，∴m2﹣7m＋10=0，
∴(m﹣2)(m﹣5)=0，∴m=2(舍去)，m=5，
∴F2(4，﹣6)．
解：(1)∵抛物线y＝ax2＋bx＋c经过A(3，0)、B(﹣1，0)，C(0，3)，
∴，解得，
∴抛物线的解析式为y＝﹣x2＋2x＋3，
∵y＝﹣(x﹣1)2＋4，
∴顶点D的坐标为(1，4)；
(2)设直线AC的解析式为y＝kx＋b，
把A(3，0)，C(0，3)代入，
得，∴，
∴直线AC的解析式为y＝﹣x＋3，
过点F作FG⊥DE于点G，
∵以A，C，E，F为顶点的四边形是以AC为边的平行四边形，
∴AC＝EF，AC∥EF，
∵OA∥FG，
∴∠OAC＝∠GFE，
∴△OAC≌△GFE(AAS)，
∴OA＝FG＝3，
设F(m，﹣m2＋2m＋3)，则G(1，﹣m2＋2m＋3)，
∴FG＝|m﹣1|＝3，
∴m＝﹣2或m＝4，
当m＝﹣2时，﹣m2＋2m＋3＝﹣5，
∴F1(﹣2，﹣5)，
当m＝4时，﹣m2＋2m＋3＝﹣5，
∴F2(4，﹣5)
综上所述，满足条件点F的坐标为(﹣2，﹣5)或(4，﹣5)；
(3)由题意，M(1，﹣1)，F2(4，﹣5)，F1(﹣2，﹣5)关于对称轴直线x＝1对称，连接F1F2交对称轴于点H，连接F1M，F2M，过点F1作F1N⊥F2M于点N，交对称轴于点P，连接PF2．则MH＝4，HF2＝3，MF2＝5，
在Rt△MHF2中，sin∠HMF2＝eq \f(3,5)，则在Rt△MPN中，sin∠PMN＝eq \f(3,5)，
∴PN＝eq \f(3,5)PM，
∵PF1＝PF2，
∴PF＋eq \f(3,5)PM＝PF2＋PN＝F1N为最小值，
∵＝eq \f(1,2)×6×4＝eq \f(1,2)×5×F1N，
∴F1N＝eq \f(24,5)，
∴PF＋eq \f(3,5)PM的最小值为eq \f(24,5)．
解：(1)y＝x2＋(m﹣2)x一2m＝(x﹣2)(x＋m)，
令y＝0，则x＝2或x＝﹣m，
∵m＞0，
∴﹣m＜0，
∴A(﹣m，0)，B(2，0)，
∴AB＝2＋m，
令x＝0，则y＝﹣2m，
∴C(0，﹣2m)，
∵△ABC的面积为8，
∴eq \f(1,2)×(2＋m)×(2m)＝8，解得m＝2或m＝﹣4(舍)；
(2)当m＝2时，y＝x2﹣4，
∵的横坐标为t，
∴T(t，t2﹣4)，
过点C作EF∥x轴，过点T作TF⊥EF交于F点，过点C作CD⊥CT交直线AT于点D，过点D作DE⊥EF交于E点，
∵∠DCT＝90°，
∴∠DCE＋∠TCF＝90°，
∵∠DCE＋∠CDE＝90°，
∴∠TCF＝∠CDE，
∴△CED∽△TFC，
∴＝＝，
∵∠ATC＝60°，
∴＝，
∵C(0，﹣4)，
∴CF＝t，TF＝t2，
∴DE＝eq \r(3)t，CE＝eq \r(3)t2，
∴D(﹣eq \r(3)t2，eq \r(3)t﹣4)，
设直线AT的解析式为y＝kx＋b，
∴，解得，
∴y＝(t﹣2)x＋2t﹣4，
∴eq \r(3)t﹣4＝(t﹣2)(﹣eq \r(3)t2)＋2t﹣4，
∴(t﹣1)2＝eq \f(2\r(3),3)；
(3)过点B作BG⊥AC交于G点，交y轴于点P，
∵A、B关于y轴对称，
∴AP＝BP，
∵∠GBA＋∠BAC＝∠ACO＋∠CAO＝90°，
∴∠ABG＝∠ACO，
∵AO＝2，CO＝4，
∴AC＝2eq \r(5)，
∴sin∠ACO＝eq \f(\r(5),5)，
∴＝，
∴eq \f(\r(5),5)CP＝GP，
∵CP＋eq \r(5)AP＝eq \r(5)(eq \f(\r(5),5)CP＋AP)＝eq \r(5)(GP＋AP)≥eq \r(5)BG，
∵cs∠ACO＝＝＝，∴BG＝，
∴CP＋eq \r(5)AP的最小值为8，
∵tan∠ACO＝＝＝，
∴OP＝1，
∴P(0，﹣1)．