福建省泉州市鲤城区福建省泉州第五中学2023-2024学年七年级下学期期中数学试题(无答案)

这是一份福建省泉州市鲤城区福建省泉州第五中学2023-2024学年七年级下学期期中数学试题(无答案)，共5页。

一、选择题（每小题4分，共40分）．在答题卡上相应题目的答题区域内作答．
1．下列各方程中，是二元一次方程的是（ ）．
A．B．C．D．
2．不等式的解集在数轴上表示正确的是（ ）．
A．B．
C．D．
3．下面4个汉字中，可以看作是轴对称图形的是（ ）．
A．中B．考C．必D．胜
4．已知，下列不等式成立的是（ ）．
A．B．C．D．
5．现有两根长度为3和4（单位：）的小木棒，下列长度的小木棒不能与它们搭成三角形的是（ ）．
A．4B．5C．6D．7
6．某人用同种正多边形瓷砖铺设无缝地板，他购瓷砖形状可能是（ ）．
A．正五边形B．正六边形C．正七边形D．正九边形
7．图中表示被撕掉一块的正边形纸片，若，则的值是（ ）．
A．5B．7C．8D．10
8．《九章算术》中记载这样一个问题：“以绳测井，若将绳三折测之，绳多四尺；若将绳四折测之，绳多一尺．问绳长、井深各几何？”题意是：用绳子测量水井深度，如果将绳子折成三等份，那么每等份井外余绳四尺；如果将绳子折成四等份，那么每等份井外余绳一尺．问绳长和井深各多少尺？下列解题方案：
①设井深为尺，列方程为；②设绳长为尺，列方程为；③设绳长、井深分别为尺，尺，列方程组为．其中正确的是（ ）．
A．①B．①②C．②③D．①②③
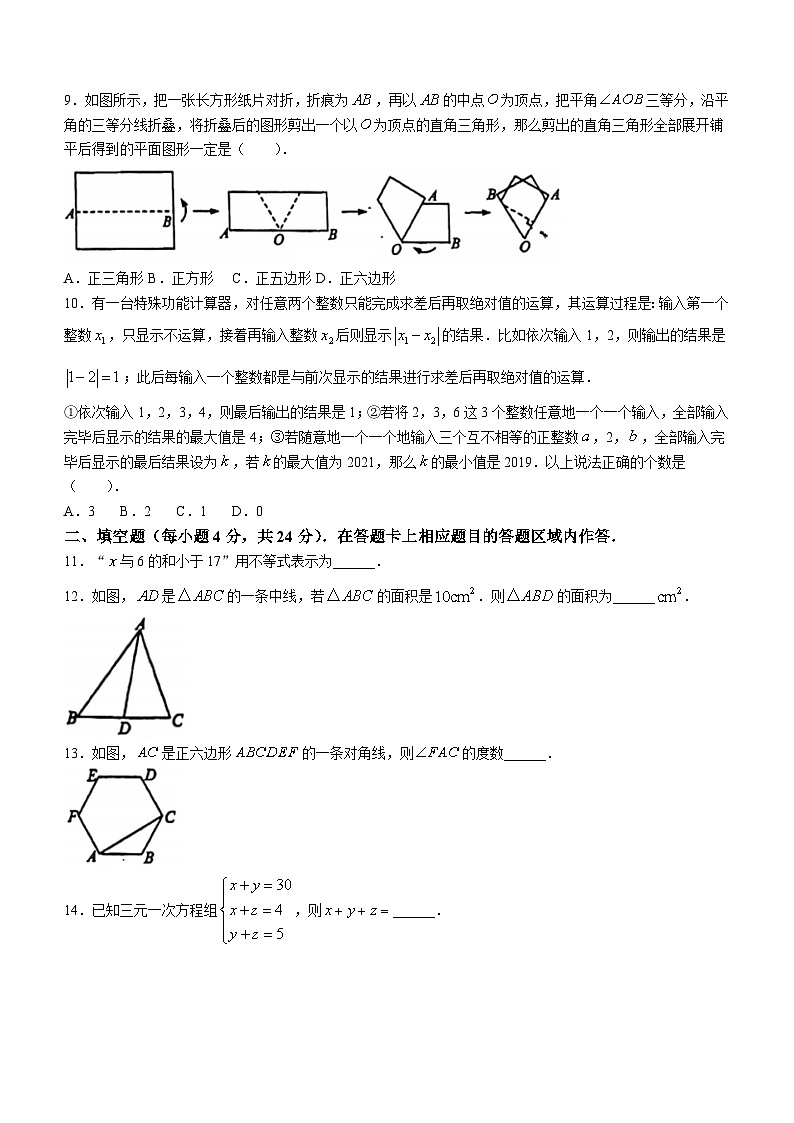
9．如图所示，把一张长方形纸片对折，折痕为，再以的中点为顶点，把平角三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以为顶点的直角三角形，那么剪出的直角三角形全部展开铺平后得到的平面图形一定是（ ）．
A．正三角形B．正方形C．正五边形D．正六边形
10．有一台特殊功能计算器，对任意两个整数只能完成求差后再取绝对值的运算，其运算过程是：输入第一个整数，只显示不运算，接着再输入整数后则显示的结果．比如依次输入1，2，则输出的结果是；此后每输入一个整数都是与前次显示的结果进行求差后再取绝对值的运算．
①依次输入1，2，3，4，则最后输出的结果是1；②若将2，3，6这3个整数任意地一个一个输入，全部输入完毕后显示的结果的最大值是4；③若随意地一个一个地输入三个互不相等的正整数，2，，全部输入完毕后显示的最后结果设为，若的最大值为2021，那么的最小值是2019．以上说法正确的个数是（ ）．
A．3B．2C．1D．0
二、填空题（每小题4分，共24分）．在答题卡上相应题目的答题区域内作答．
11．“与6的和小于17”用不等式表示为______．
12．如图，是的一条中线，若的面积是．则的面积为______．
13．如图，是正六边形的一条对角线，则的度数______．
14．已知三元一次方程组，则______．
15．若关于的不等式组的解集为，且关于的方程有非负整数解，则满足条件的所有整数的和为______．
16．如图，，点、分别在射线、上，，的面积为12，是直线上的动点，点关于对称的点为，点关于对称的点为，当点在直线上运动时，的面积最小值为______．
三、解答题（共86分）．在答题卡上相应题目的答题区域内作答．
17．（8分）解方程组：．
18．（8分）解不等式组，并在数轴上表示其解集且写出它的所有的非正整数解．
19．（8分）已知一个多边形的边数为，若这个多边形的每个内角都比与它相邻的外角的4倍多，求这个多边形对角线的总条数．
20．（8分）中，，，是高，是三角形的角平分线．求的度数．
21．（8分）已知关于，的二元一次方程组与方程组有相同的解．
（1）求这两个方程组的相同解；
（2）求的值．
22．（10分）我市某校为了落实“阳光体育活动”，在七年级开展了篮球赛．比赛规则是：七年级10个班级每个班级派出一支队伍参赛，赛制采用的是单循环积分赛（每个班级都与其他9个班级进行一场比赛），胜一场记2分，负一场记1分，然后按照积分高低进行排名．赛程过半，小明所在的班级已经进行了5场比赛，积9分．
（1）求小明所在班级胜、负的场次各是多少；
（2）根据分析，总积分超过15分才能确保进入前两名，小明的班级若想进入前两名在剩下的比赛中至少还要取得几场胜利？
23．（10分）数学小组的同学发现，折纸中蕴含着许多数学问题．现有一张三角形纸片，点，分别是边，上的点，若沿直线折叠，点的对应点为点，且点在直线的右侧．
（1）若如图1所示，点恰好在边上，则与的数量关系是______．
（2）记，，且，的度数均不为0，试通过折痕的变化，探索，和之间的数量关系．
24．（12分）某学校实践课准备用图甲所示的型正方形板材和型长方形板材，制作成图乙所示的竖式和橫式两种无盖箱子。
（1）若学校现有库存型板材55张，型板材120张，用这批板材制作两种类型的箱子，恰好将库存板材用完时，能制作出竖式和横式的箱子各多少只？
（2）现有型板材162张，型板材340张，若要做这两种箱子共100个，请问有哪几种生产方案？
（3）若学校新购得张规格为的型正方形板材，将其全部切割成型或型板材（不计损耗），用切割成的板材制作两种类型的箱子，要求竖式箱子制作20只，且材料恰好用完，求的最小值？
25．（14分）
【引入概念】
概念1：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
概念2：从不等边三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形．若分成的两个小三角形中一个是满足有两个角相等的三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．
【理解概念】
（1）如图1，在中，，，请写出图中两对“等角三角形”．①______；②______．
（2）如图2，在中，为角平分线，，．请你说明是的等角分割线．
【应用概念】
（3）在中，若，为的等角分割线，求度数．