






§4.6 函数y=Asin(ωx+φ) 课件-2025高考数学一轮复习
展开1.结合具体实例,了解y=Asin(ωx+φ)的实际意义;能借助图象理解参数ω,φ,A的意义,了解参数的变化对函数图象的影响.2.会用三角函数解决简单的实际问题,体会可以利用三角函数构建刻画事物周期变化的数学模型.
第一部分 落实主干知识
第二部分 探究核心题型
1.简谐运动的有关概念已知函数y=Asin(ωx+φ)(A>0,ω>0),x≥0
2.用“五点法”画y=Asin(ωx+φ)(A>0,ω>0)一个周期内的简图时,要找五个特殊点
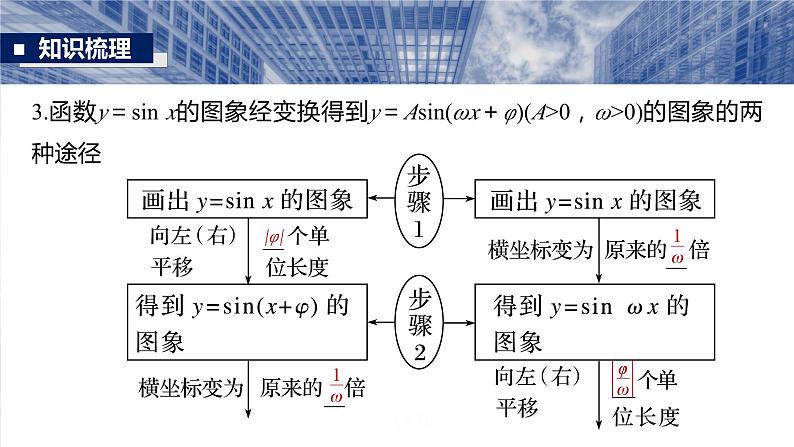
3.函数y=sin x的图象经变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象的两种途径
函数y=Asin(ωx+φ)+k的图象平移的规律:“左加右减,上加下减”.
1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)函数f(x)=Asin(ωx+φ)(A≠0)的最大值为A,最小值为-A.( )
即12点时潮水的高度是1 m.
题型一 函数y=Asin(ωx+φ)的图象及变换
(2)如果平移前后两个图象对应的函数的名称不一致,那么应先利用诱导公式化为同名函数,ω为负时应先变成正值.
A.2 B.3 C.6 D.9
即ω=3k,k∈Z,∴ω不可能为2.
题型二 由图象确定y=Asin(ωx+φ)的解析式
例2 (1)(多选)(2024·邢台模拟)函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,0<φ<π)在一个周期内的图象如图所示,则
由函数f(x)=2sin(ωx+φ)的部分图象,设A(x1,2),B(x2,-2),其中x1
(3)求φ.常用方法如下:①代入法:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入.②五点法:确定φ值时,往往以寻找“五点法”中的特殊点作为突破口.
所以f(x)=sin(4x+φ),
题型三 三角函数图象、性质的综合应用
例3 (1)(多选)筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用(图1),明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图2).一半径为2米的筒车水轮如图3所示,水轮圆心O距离水面1米,已知水轮每60秒逆时针匀速转动一圈,如果当水轮上点P从水中浮现时(图3中点P0)开始计时,则下列结论正确的是A.点P再次进入水中时用时30秒B.当水轮转动50秒时,点P处于最低点C.当水轮转动150秒时,点P距离水面2米D.点P第二次到达距水面(1+ )米时用时25秒
建立如图所示的平面直角坐标系,设点P距离水面的高度H=Asin(ωt+φ)+B(A>0,ω>0),
解得t=60k+15或t=60k+25(k∈N).
所以f(x)=-sin 2x,
(1)研究y=Asin(ωx+φ)的性质时可将ωx+φ视为一个整体,利用换元法和数形结合思想进行解题.(2)方程根的个数可转化为两个函数图象的交点个数.(3)三角函数模型的应用体现在两方面:一是已知函数模型求解数学问题;二是把实际问题抽象转化成数学问题,利用三角函数的有关知识解决问题.
跟踪训练3 (1)某地农业监测部门统计发现:该地区近几年的生猪收购价格每四个月会重复出现.如表所示是今年前四个月的统计情况.
选用一个正弦型函数来近似描述收购价格(单位:元/斤)与相应月份之间的函数关系为____________________________.
设y=Asin(ωx+φ)+B(A>0,ω>0),由题意得A=1,B=6,T=4,
因为当x=1时,y=6,
故m的取值范围是(-2,-1).
∴ω=2,f(x)=sin(2x+φ),
再将所得曲线上所有点的横坐标伸长到原来的2倍,得到f(x)的图象,
则ω=2+8k>0,k∈Z,∴当k=0时,ω的最小值为2.
由f(x)=g(x),可得
二、多项选择题7.如图是函数y=sin(ωx+φ)的部分图象,则该函数的解析式为
由题图可知,函数的最小正周期
∵函数f(x)的最小正周期为π,
因为函数g(x)是奇函数,
所以f(x)在[0,2 024π]内有8 096条对称轴.
12.风车发电是指把风的动能转化为电能.如图,风车由一座塔和三个叶片组成,每两个叶片之间的夹角均为120°.现有一座风车,塔高60米,叶片长度为30米.叶片按照逆时针方向匀速转动,并且6秒旋转一圈,风车
开始旋转时,某叶片的一个端点P在风车的最低点(P离地面30米),设点P离地面的距离为S(米),转动时间为t(秒),则S与t之间的函数解析式为____________________,一圈内点P离地面的高度不低于45米的时长为________秒.
故一圈内点P离地面的高度不低于45米的时长为4秒.
(1)求函数y=f(x)的解析式;
(1)求函数y=h(x)的最小正周期和单调递增区间;
由题意知g(x)=2sin(x+φ),
15.(2023·大连模拟)如图,函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π) 的图象与坐标轴交于点A,B,C,直线BC交f(x)的图象于点D,点O(坐标原点)为△ABD的重心(三条边中线的交点),其中A(-π,0),则OB等于
根据题意可知,点C是f(x)的一个对称中心,又直线BC交f(x)的图象于点D,利用对称性可知B,D两点关于C点对称.不妨设B(xB,yB),C(xC,yC),D(xD,yD),
将函数f(x)=asin x+bcs x(a,b∈R且b≠0)的图象上各点的横坐标伸长为原来的2倍,
因为h(x)为奇函数,图象关于原点对称,
高中数学人教A版 (2019)必修 第一册5.6 函数 y=Asin( ωx + φ)图文课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册5.6 函数 y=Asin( ωx + φ)图文课件ppt,共34页。PPT课件主要包含了复习回顾,教学目标,教学重难点,取A1,问题5,横坐标不变,步骤1,步骤4,步骤3,步骤2等内容,欢迎下载使用。
新高考数学一轮复习讲练测课件第4章§4.6函数y=Asin(ωx+φ) (含解析): 这是一份新高考数学一轮复习讲练测课件第4章§4.6函数y=Asin(ωx+φ) (含解析),共60页。PPT课件主要包含了落实主干知识,探究核心题型,课时精练,所以1ω2,因为1ω2,-2-1,-21,因为x∈01,由题意可知等内容,欢迎下载使用。
高考复习 4.6 函数y=A sin (ωx+φ)的图象及应用课件PPT: 这是一份高考复习 4.6 函数y=A sin (ωx+φ)的图象及应用课件PPT,共48页。PPT课件主要包含了sinωx,sinωx+φ,答案C,答案D,答案BD,答案B,答案ABC,答案A,答案AD等内容,欢迎下载使用。












