河北省邢台市多校2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份河北省邢台市多校2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含河北省邢台市多校2023-2024学年七年级下学期期中数学试题原卷版docx、河北省邢台市多校2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。

2.考生完成试卷后，务必从头到尾认真检查一遍．
一、选择题（本大题共12个小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1. 4的平方根是（ ）
A. ±2B. 2C. ﹣2D. 16
【答案】A
【解析】
【分析】根据平方根的定义，求数a的平方根，也就是求一个数x，使得x2=a，则x就是a的一个平方根．
【详解】∵（±2 ）2=4，
∴4的平方根是±2，
故选A．
【点睛】本题主要考查平方根的定义，熟练掌握平方根的定义是解题的关键.
2. 下列各数是无理数的为（ ）
A. 0B. C. D.
【答案】D
【解析】
【分析】无理数就是无限不循环小数，理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数，由此即可判定选择项．
本题主要考查了无理数的定义，其中初中范围内学习的无理数有：等；开方开不尽的数；以及像，等数．
【详解】解：
无理数是
故选：D．
3. 嘉淇一家要到革命圣地西柏坡参观，如图，西柏坡位于嘉淇家南偏西的方向上，处，则嘉淇家位于西柏坡的（ ）
A. 南偏西方向，处B. 南偏东方向，处
C. 北偏东方向，处D. 北偏东方向，处
【答案】C
【解析】
【分析】本题主要考查方向角，理解方向角的定义是正确解答的关键．根据方向角的定义可得答案．
【详解】解：如图可得：
∵西柏坡位于嘉淇家南偏西的方向，处，
∴嘉淇家位于西柏坡的北偏东方向，处．
故选：C．
4. 下列各式中正确的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了平方根和立方根的概念，正确理解平方根和立方根的概念是解答本题的关键．“如果，则x叫做a的平方根，记作，叫做a的算术平方根．”“如果，则x叫做a的立方根，记作．”，根据概念即可解答本题．
【详解】选项A，表示9的算术平方根， ，所以该选项不正确，不符合题意；
选项B，表示的立方根，，所以该选项正确，符合题意；
选项C，表示16的平方根，，所以该选项不正确，不符合题意；
选项D，表示的算术平方根，，所以该选项不正确，不符合题意．
故选：B．
5. 如图，点E在的延长线上，下列条件中能判断的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】本题考查了平行线的判定定理，熟练掌握平行线的判定定理是解题的关键．
根据平行线的判定定理对各选项分别进行判断即可．
【详解】解：A中可判断，故此选项错误；
B中可判断，故此选项错误；
C中可判断，故此选项错误；
D中可判断AB∥CD，故此选项正确；
故选：D．
6. 过点和作直线，则直线AB（ ）
A. 与x轴平行B. 与y轴平行C. 与x轴相交D. 与x轴、y轴均相交
【答案】A
【解析】
【分析】本题考查坐标系下点的特征．根据和的纵坐标相同，即可得到直线轴．熟练掌握与x轴平行的直线上的点的纵坐标相同，是解题的关键．
【详解】解：∵点和的纵坐标相同，
∴直线轴；
故选A．
7. 如图，直线，相交于点O，下面是推导对顶角相等的过程：因为，，所以，其推理依据是（ ）
A. 同角的余角相等B. 等角的余角相等
C. 同角的补角相等D. 等角的补角相等
【答案】C
【解析】
【分析】本题考查了补角的性质，注意同角或等角的补角相等，在本题中要注意判断是“同角”还是“等角”．
【详解】解：由题意得：推理依据是同角的补角相等，
故选：C．
8. 如图，数轴上有M，N，P，Q四点，则这四点中所表示的数最接近的是（ ）
A. 点MB. 点NC. 点PD. 点Q
【答案】B
【解析】
【分析】本题考查的是无理数与数轴．先估算的值，结合数轴即可得出答案．
【详解】解：∵，
∴，
∴最接近的是点N
故选：B．
9. 如图是嘉淇答卷，嘉淇的得分为（ ）
A. 2分B. 4分C. 6分D. 8分
【答案】D
【解析】
【分析】本题考查了相反数，平方根，立方根，算术平方根，解题的关键是掌握这几个定义；
根据只有符号不同的两个数叫做互为相反数，立方根、平方根的定义判断即可．
【详解】的相反数是，正确；
表示的算术平方根，错误，负数，没有算术平方根；
0.9的平方根是，错误；
，正确；
0平方根和立方根相同，正确；
故选：D．
10. 如图，点A，B的坐标分别为，，将线段平移至的位置，点的坐标为，则点的坐标为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了图形的平移与坐标，根据对应点的坐标确定平移方式即可求解．
【详解】解：由、可得平移方式为：向右平移3个单位长度，向上平移个单位长度，
∴的坐标为．
故选：C．
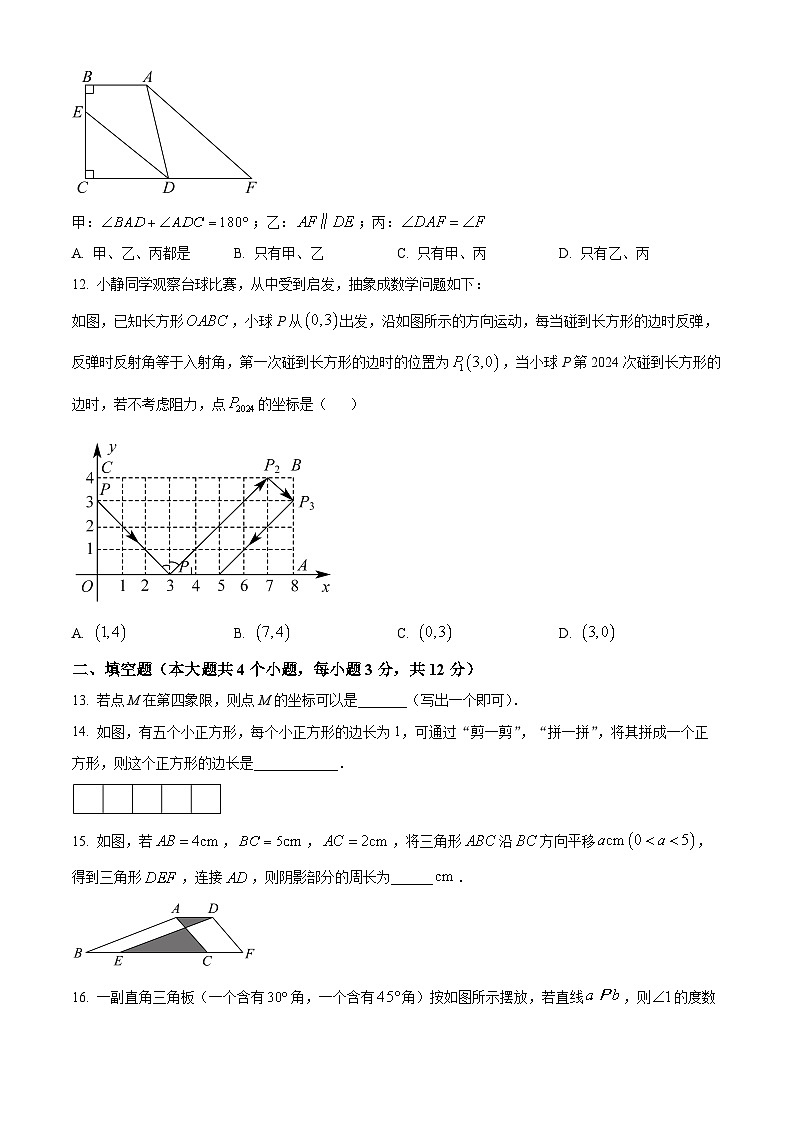
11. 如图，于点B，于点C，平分交于点E，F为线段延长线上一点，．现有以下三个结论，则正确的结论（ ）

甲：；乙：；丙：
A. 甲、乙、丙都是B. 只有甲、乙C. 只有甲、丙D. 只有乙、丙
【答案】A
【解析】
【分析】依据于点B，于点C，即可得到，进而得出，，再根据，即可得出，依据角平分线的定义，即可得到．
【详解】解：如图，
∵于点B，于点C，
∴，
∴，
∴，（甲正确），
又∵，
∴，
∴（乙正确），
∴，，
∵平分，
∴，
∴（丙正确）；

故选：A．
【点睛】本题主要考查了平行线的判定与性质及角平分线的定义，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
12. 小静同学观察台球比赛，从中受到启发，抽象成数学问题如下：
如图，已知长方形，小球P从出发，沿如图所示的方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，第一次碰到长方形的边时的位置为，当小球P第2024次碰到长方形的边时，若不考虑阻力，点的坐标是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了点坐标规律性变化，解决此类问题的关键是找到待求量与序号之间的关系．按照反弹时反射角等于入射角，画出图形，可以发现每六次反射一个循环，最后回到起始点，然后计算2024有几个6即可求出对应点的坐标．
【详解】解：按照反弹时反射角等于入射角，画出图形，如下图：
，，，，，，，…，
通过以上变化规律，可以发现每六次反射一个循环，
∵，
∴，
∴点的坐标是．
故选：B．
二、填空题（本大题共4个小题，每小题3分，共12分）
13. 若点M在第四象限，则点M的坐标可以是_______（写出一个即可）．
【答案】（答案不唯一）
【解析】
【分析】本题考查了点坐标，熟练掌握第四象限内的点横坐标大于0，纵坐标小于0是解题关键．根据第四象限内的点的横坐标大于0，纵坐标小于0，由此即可得．
【详解】∵第四象限内的点横坐标大于0，纵坐标小于0
∴点M的坐标可以是
故答案为：（答案不唯一）．
14. 如图，有五个小正方形，每个小正方形的边长为1，可通过“剪一剪”，“拼一拼”，将其拼成一个正方形，则这个正方形的边长是____________．
【答案】
【解析】
【分析】由面积不变求出拼成的正方形的面积，再利用公式计算边长即可．
【详解】解：∵拼成的正方形的面积为，
∴这个正方形的边长是，
故答案为：．
【点睛】此题考查了有理数的乘方和乘法计算，算术平方根的实际应用，正确理解面积不变规律是解题的关键．
15. 如图，若，，，将三角形沿方向平移，得到三角形，连接，则阴影部分的周长为______．

【答案】11
【解析】
【分析】本题考查的是平移的性质，掌握平移不改变图形的形状和大小、经过平移，对应点所连的线段平行且相等，对应线段平行且相等是解答本题的关键．根据平移的性质得到，根据周长公式计算，得到答案．
【详解】由平移的性质，可知：

∴，
∴阴影部分的周长为
故答案为：11．
16. 一副直角三角板（一个含有角，一个含有角）按如图所示摆放，若直线，则的度数为_______．
【答案】##15度
【解析】
【分析】本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，内错角相等；
先根据平行线的性质得到，再根据三角形外角性质进行计算即可．
【详解】解：如图所示，延长一直角边交直线a于一点，
∵
∴
由三角形外角性质，可得
∴
故答案为：．
三、解答题（本大题共8个小题，共72分．解答应写出文字说明、证明过程或演算步骤）
17. 按要求完成下列各小题．
（1）计算：；
（2）求x的值：．
【答案】（1）
（2）
【解析】
【分析】本题考查的是求解算术平方根，立方根，利用立方根的含义解方程，掌握平方根与立方根的含义是解本题的关键；
（1）先分别求解算术平方根，立方根，再合并即可；
（2）利用立方根的含义解方程即可．
【小问1详解】
解：原式
【小问2详解】
解：
解得：
18. 如图，每个小正方形网格的边长表示50米，A同学上学时从家中出发，先向东走250米，再向北走50米就到达学校．
（1）请你以学校为坐标原点，向东为x轴正方向，向北为y轴正方向，在图中建立平面直角坐标系；
（2）利用（1）中建立的平面直角坐标系，以1米为1个单位长度，写出B同学家的坐标，若C同学家的坐标为，请在图上标出C同学家的位置．
【答案】（1）见解析 （2），见解析
【解析】
【分析】此题考查了利用点坐标确定直角坐标系，根据点的位置得到点的坐标，由点的坐标描点，正确掌握点与坐标的关系是解题的关键．
（1）根据同学到学校的方向与距离确定学校在点向右5个网格，再向上1个网格的位置，即可建立直角坐标系，根据点在坐标系中的位置得到坐标；
（2）根据点的坐标知点在第二象限，到x轴3个网格的距离，到y轴1个网格的距离，由此描出点．
【小问1详解】
如图所示，建立直角坐标系：
【小问2详解】
由题意可得：；
C同学家如图所示．
19. 将下列证明过程补充完整．
已知：如图，，，求证：．
证明：∵（已知），
∴（__________________），
∴____________（__________________）．
∵（已知），
∴（等量代换），
∴____________（内错角相等，两直线平行），
∴（__________________）．
【答案】内错角相等，两直线平行；，两直线平行，内错角相等；；两直线平行，同位角相等
【解析】
【分析】此题考查平行线的性质和判定定理，先证明，推出，再证明，推出据此即可证明．
【详解】证明：∵（已知），
∴（内错角相等，两直线平行），
∴（两直线平行，内错角相等）．
∵（已知），
∴（等量代换），
∴（内错角相等，两直线平行），
∴（两直线平行，同位角相等）．
20. 如果一个正数m的两个平方根分别是和，n是的立方根．
（1）求m和n的值．
（2）求的算术平方根．
【答案】（1），； （2）6
【解析】
【分析】（1）根据一个正数的两个平方根互为相反数求出a的值，利用平方根和立方根即可求解；
（2）将（1）中结果代入，然后求算术平方根即可．
【小问1详解】
解：∵一个正数m的两个平方根分别是和，
∴，
解得：，
∴，
∴，
∵n是的立方根，
∴；
【小问2详解】
由（1）得，，
∴，
∴的算术平方根为6．
【点睛】本题考查了平方根的性质，立方根的性质．解决本题的关键是求出a．
21. 如图，已知直线，相交于点O，平分，．
（1）如果，求，的度数；
（2）如果，求的度数；
（3）写出图中所有与互余的角：______________．
【答案】（1）；
（2）
（3）图中所有与互余角，；
【解析】
【分析】此题主要考查了角的计算，对顶角的性质，互为余角的定义，角平分线的定义，理解对顶角
的性质，互为余角的定义，角平分线的定义，熟练掌握角的计算是解决问题的关键．
（1）先由对顶角相等得，根据角平分线的定义得，再由得，最后根据即可求解；
（2）根据，，可求出，然后根据平分，即可求解；
（3）根据得，再根据和平分即可求解．
【小问1详解】
解：∵直线，相交于点O，
∴
∵平分，
∴
∵
∴
∴
∵，
∴
∴ ，
∴；
【小问2详解】
∵，
∴
∵平分，
∴
∵
∴
∴
【小问3详解】
∵
∴
∴
∴与互余；
∵，
∴
∵平分，
∴
∴
∴与互余；
∴图中所有与互余的角，；
22. 小明制作了一张面积为的正方形贺卡想寄给朋友．现有一个长方形信封如图所示，长、宽之比为，面积为．

（1）求长方形信封的长和宽；
（2）小明能将贺卡不折叠就放入此信封吗？请通过计算给出判断．
【答案】（1）长为，宽为
（2）小明能将这张贺卡不折叠就放入此信封，见解析
【解析】
【分析】（1）设长方形信封的长为，宽为，根据面积为列方程求解即可；
（2）先求出贺卡的边长，然后与信封的宽比较即可．
【小问1详解】
∵信封的长、宽之比为，
∴设长方形信封的长为，宽为，
由题意得，
∴（负值舍去），
∴长方形信封的长为，宽为；
【小问2详解】
面积为的正方形贺卡的边长是．
∵，所以，
∴，即信封的宽大于正方形贺卡的边长，
∴小明能将这张贺卡不折叠就放入此信封．
【点睛】本题考查算术平方根的应用，以及无理数的估算，关键是掌握由算术平方根的定义求出正方形贺卡的边长．
23. 三角形在平面直角坐标系中的位置如图所示．
（1）分别写出点A，B，C的坐标；并求三角形的面积；
（2）过点作直线轴，若点P在直线l上运动，连接，当线段长度最小时，直接写出此时点P的坐标；
（3）若点Q在y轴上，且三角形与三角形的面积相等，求点Q的坐标．
【答案】（1），，；
（2）
（3）或
【解析】
【分析】本题考查坐标系中点的坐标，点到直线的最短距离以及三角形的面积，熟练掌握以上知识点是解题的关键．
（1）根据坐标系中直接写出各点坐标即可，利用网格求出三角形的面积即可；
（2）根据点到直线的最短距离求出点P的坐标即可；
（3）注意区分当点Q在y轴上时与点B的位置关系，分情况计算即可．
【小问1详解】
解：由坐标系可得：，，；
【小问2详解】
解：如图
当时，长度最小
∵
∴；
【小问3详解】
解：设
∵三角形与三角形的面积相等，
∴，解得：或8
∴或
24. 已知直线，直线与，分别交于点E，F，.将一个直角三角板按如图1所示放置，使点Q，O分别在直线，上，，，，．
（1）若、分别求与的度数；
（2）求的度数；
（3）将直角三角板沿向右平移．
①如图2，当点Q与点E重合时，若恰好平分，求的值；
②作的平分线，交直线于点G，在整个平移过程中，直接写出的度数（用含的式子表示）．
【答案】（1）；
（2）
（3）②或
【解析】
【分析】（1）根据，可得，再根据补角的定义即可求出；根据可得，再根据补角的定义即可求出；
（2）先根据图表示出，，进而根据，可得，即可求解；
（3）①根据题意分别表示出，根据三角形内角和定理即可求解；②分情况讨论：当点Q在直线左侧；当点Q在直线右侧，根据平行线的性质和角平分线的性质求解即可．
【小问1详解】
解：∵，
∴，
∵
∴；
∵
∴
∴；
【小问2详解】
解：由图可得：
∵，，
∴，
∴
∵
∴
∴；
【小问3详解】
① 解：由图可得：
∵，
∴
∵，
∴
∴
∵
∴
∵恰好平分，
∴
在中，
解得：；
②当点Q在直线左侧，
∵，
∴，
∵
∴；
∵，平分平分，
∴，
∴；
当点Q在直线右侧，
∵，
∴，
∵
∴；
∴
∵平分平分，
∴
∵
∴；
【点睛】本题考查利用平行线的性质，三角形的内角和定理，角平分线的性质等．熟练掌握平行线的性质，是解题的关键．
判断题（每小题2分）姓名：嘉淇
1.的相反数是；（√）
2.表示的算术平方根；（√）
3.0.9平方根是；（×）
4.；（√）
5.0的平方根和立方根相同．（√）