



初中人教版26.1.2 反比例函数的图象和性质完美版ppt课件
展开反比例函数的图象及性质
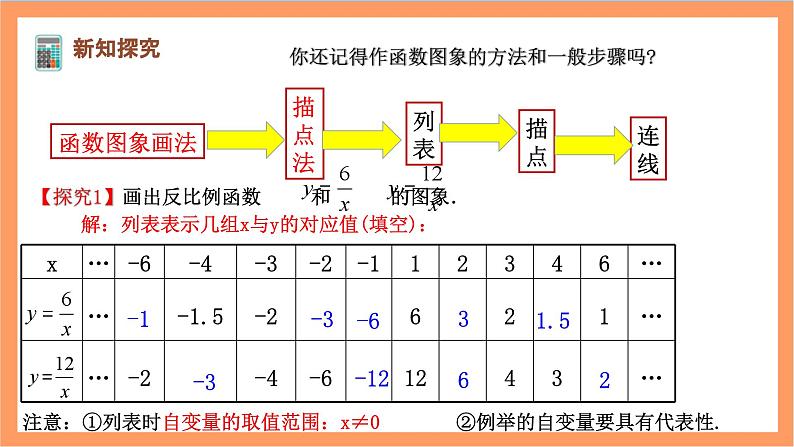
你还记得作函数图象的方法和一般步骤吗?
解:列表表示几组x与y的对应值(填空):
注意:①列表时自变量的取值范围:x≠0
②例举的自变量要具有代表性.
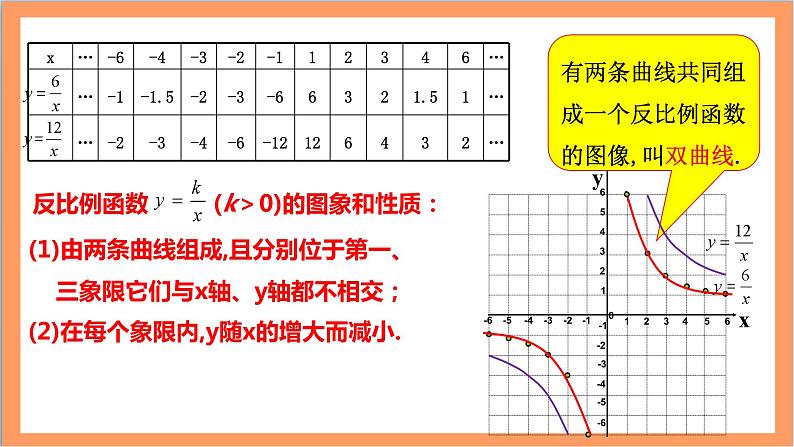
有两条曲线共同组成一个反比例函数的图像,叫双曲线.
(1)由两条曲线组成,且分别位于第一、 三象限它们与x轴、y轴都不相交;
(2)在每个象限内,y随x的增大而减小.
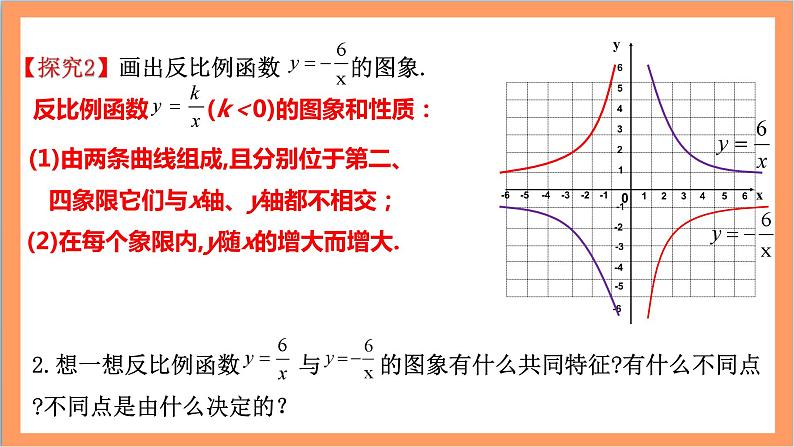
(1)由两条曲线组成,且分别位于第二、 四象限它们与x轴、y轴都不相交;
(2)在每个象限内,y随x的增大而增大.
(1)当k>0时,双曲线的两支分别位于第一、三象限,在每一个象限内, y随x的增大而减小;
k的正负决定反比例函数所在的象限和增减性.
(2)当k<0时,双曲线的两支分别位于第二、四象限,在每一个象限内, y随x的增大而增大.
|k|越大,双曲线离坐标轴越远.
【例1】反比例函数 的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0<x2,则下列结论正确的是( ) A.y1<y2<0 B.y1<0<y2 C.y1>y2>0 D.y1>0>y2
已知反比例函数y=(a-1)xa2+a-7,在每一象限内,y随x的增大而增大,求a的值.
解:由题意得a2+a-7=-1,且a-1<0.
解得:a1=-3,a2=2且a<1.
在每个象限内,y随x的增大而减小
在每个象限内,y随x的增大而增大
对称轴:________.对称中心:____.
既是轴对称图形,又是中心对称图形.
1.双曲线向四边无限延伸,与坐标轴没有交点.
2.|k|越大,双曲线离坐标轴越远
2.已知反比例函数 图象如上图,则实数m的取值范围是( ) A.m>1 B.m>0 C.m<1 D.m<0 3.反比例函数 的图象中,当x>0时,y随x的增大而增大,则实数k的取值范围是( ) A.k<3 B.k≤3 C.k>3 D.k≥3 4.已知A(-1,y1),B(2,y2)两点在双曲线 上,且y1>y2,则m的的取值范围是( ) A.m>0 B.m<0 C.m>-1.5 D.m<-1.5
5.函数y=kx-k与 的图象大致是( )
利用反比例函数图象的对称性求值
解:由题意知,在图象的每一支上,y随x的增大而减小.
故a的取值范围为:-1<a<1.
①当这两点在图象的同一支上时,
②当这两点分别位于图象的两支上时,
∴a-1<0,a+1>0,
∴必有y1<0<y2.
初中数学第二十六章 反比例函数26.1 反比例函数26.1.2 反比例函数的图象和性质教课ppt课件: 这是一份初中数学<a href="/sx/tb_c102626_t3/?tag_id=26" target="_blank">第二十六章 反比例函数26.1 反比例函数26.1.2 反比例函数的图象和性质教课ppt课件</a>,共22页。PPT课件主要包含了学习目标,xyk等内容,欢迎下载使用。
人教版九年级下册26.1.2 反比例函数的图象和性质课前预习课件ppt: 这是一份人教版九年级下册26.1.2 反比例函数的图象和性质课前预习课件ppt,共33页。PPT课件主要包含了学习目标,课时讲解,课时流程,知识点,反比例函数的图象,感悟新知,解列表,反比例函数的性质,k<2等内容,欢迎下载使用。
人教版26.1.2 反比例函数的图象和性质课前预习课件ppt: 这是一份人教版26.1.2 反比例函数的图象和性质课前预习课件ppt,共1页。













