2024年广东省汕头市金平区汕樟中学中考一模数学试题（原卷版+解析版）

这是一份2024年广东省汕头市金平区汕樟中学中考一模数学试题（原卷版+解析版），文件包含2024年广东省汕头市金平区汕樟中学中考一模数学试题原卷版docx、2024年广东省汕头市金平区汕樟中学中考一模数学试题解析版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。

1. 下列食品标识中，既是轴对称图形又是中心对称图形的是（ ）
A. 绿色饮品B. 绿色食品
C. 有机食品D. 速冻食品
2. 在下列方程中，是一元二次方程的是（ ）
A. B. C. D.
3. 直线关于原点对称的直线为（ ）
A B. C. D.
4. 下列二次根式中，属于最简二次根式的是（ ）
A. B. C. D.
5. 下列关于二次根式的计算，正确的是（ ）
A. B. C. D.
6. 若方程x2+3x+c＝0没有实数根，则c的取值范围是（ ）
A. c＜B. c＜C. c＞D. c＞
7. 下列各式计算正确的是（ ）
A. a2+a2＝a4B. 2a2×2a2＝2a4
C. （a﹣b）2＝a2﹣b2D. （4ab+1）（4ab﹣1）＝16a2b2﹣1
8. 如图，在△ABC，∠C＝90°，AD平分∠BAC交CB于点D，过点D作DE⊥AB，垂足恰好是边AB的中点E，若AD＝3cm，则BE的长为（ ）

A. cmB. 4cmC. 3cmD. 6cm
9. 如图，菱形OABC的边OA在平面直角坐标系中的x轴上，，，则点C的坐标为（ ）
A B. C. D.
10. 如图，抛物线与x轴交于A，B两点，与y轴交于点．已知点A在与之间（不包含这两点），抛物线的顶点为D，对称轴是直线．下列结论中正确的个数是（ ）
①； ②； ③；
④若三点，，均在函数图象上，则；
⑤若，则是等边三角形．
A. 2B. 3C. 4D. 5
二．填空题（共5小题，满分15分，每小题3分）
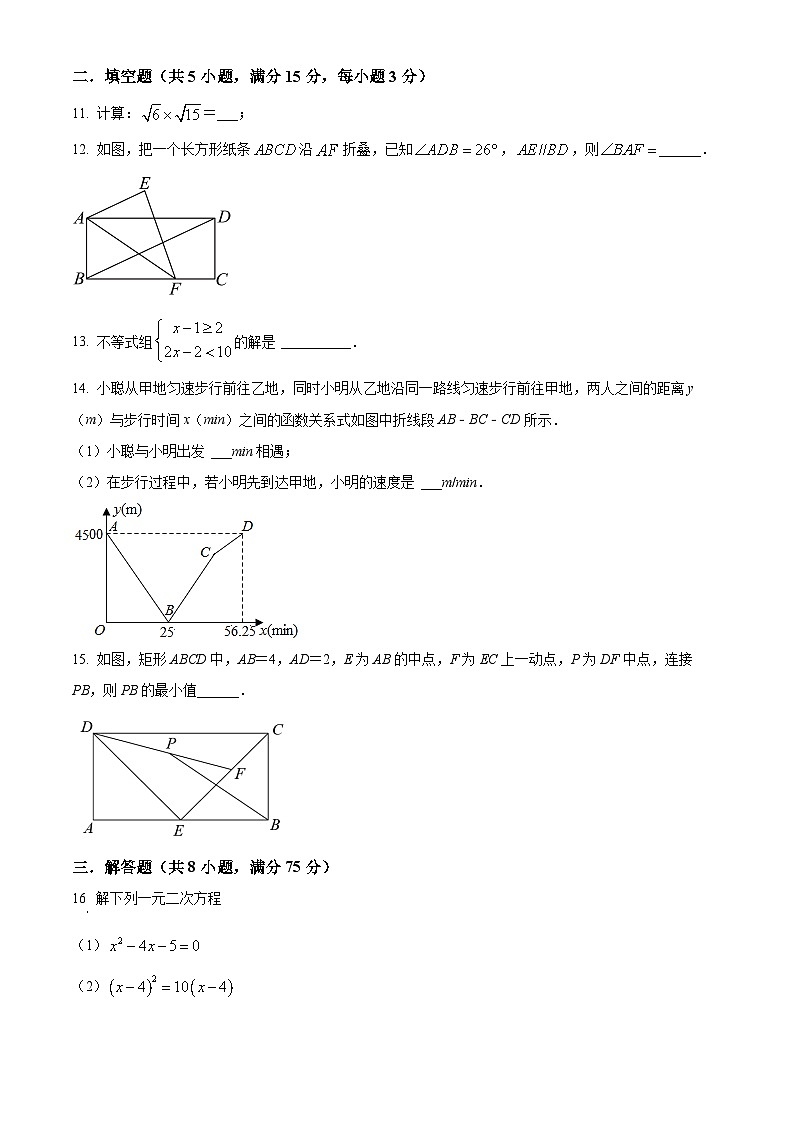
11. 计算：＝___；
12. 如图，把一个长方形纸条沿折叠，已知，，则______．
13. 不等式组的解是 __________．
14. 小聪从甲地匀速步行前往乙地，同时小明从乙地沿同一路线匀速步行前往甲地，两人之间的距离y（m）与步行时间x（min）之间的函数关系式如图中折线段AB﹣BC﹣CD所示．
（1）小聪与小明出发 ___min相遇；
（2）在步行过程中，若小明先到达甲地，小明的速度是 ___m/min．
15. 如图，矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值______．
三．解答题（共8小题，满分75分）
16 解下列一元二次方程
（1）
（2）
17. 已知，求的值．
18. 如图，在平面直角坐标系中，的三个顶点都在格点上，已知，，．
（1）作出关于x轴对称的
（2）作出绕点O逆时针旋转90°后的；
（3）将先向左平移4个单位，再向下平移5个单位，作出平移后．
19. 如图，AB是⊙O的弦，OC⊥OA，交AB与点P，且PC=BC，求证：BC是⊙O的切线．
20. 如图，直角三角形，直角顶点C在直线l上，分别过点A、B作直线l的垂线，垂足分别为点D和点E．．
（1）求证：；
（2）若设的三边分别为a、b、c，试用此图证明勾股定理．
21. 如图，正比例函数的图像与反比例函数的图像都经过点．
（1）求点A的坐标和反比例函数表达式．
（2）若点在该反比例函数图像上，且它到y轴距离小于3，请根据图像直接写出n的取值范围．
22. 如图，在中，，以为直径的交，边于点D、F．过点D作于点E．
（1）求证：是的切线；
（2）求证：；
（3）若半径为5，且，求的长．
23. 如图，二次函数交x轴于点和交y轴于点C．
（1）求二次函数的解析式；
（2）如图，在第一象限有一点M，到O点距离为2，线段与夹角为，且，连接，求的长度；
（3）对称轴交抛物线于点D，交交于点E，在对称轴的右侧有一动直线l垂直于x轴，交线段于点F，交抛物线手点P，动直线在沿x轴正方向移动到点B的过程中，是否存在点P，使得以点P，C，F为顶点的三角形与相似？如果存在，求出点P的坐标；如果不存在，请说明理由．