广西壮族自治区防城港市上思县教育科学研究所2023-2024学年七年级下学期4月月考数学试题（原卷版+解析版）

这是一份广西壮族自治区防城港市上思县教育科学研究所2023-2024学年七年级下学期4月月考数学试题（原卷版+解析版），文件包含广西壮族自治区防城港市上思县教育科学研究所2023-2024学年七年级下学期4月月考数学试题原卷版docx、广西壮族自治区防城港市上思县教育科学研究所2023-2024学年七年级下学期4月月考数学试题解析版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
数学
时间：120分钟 满分：120分
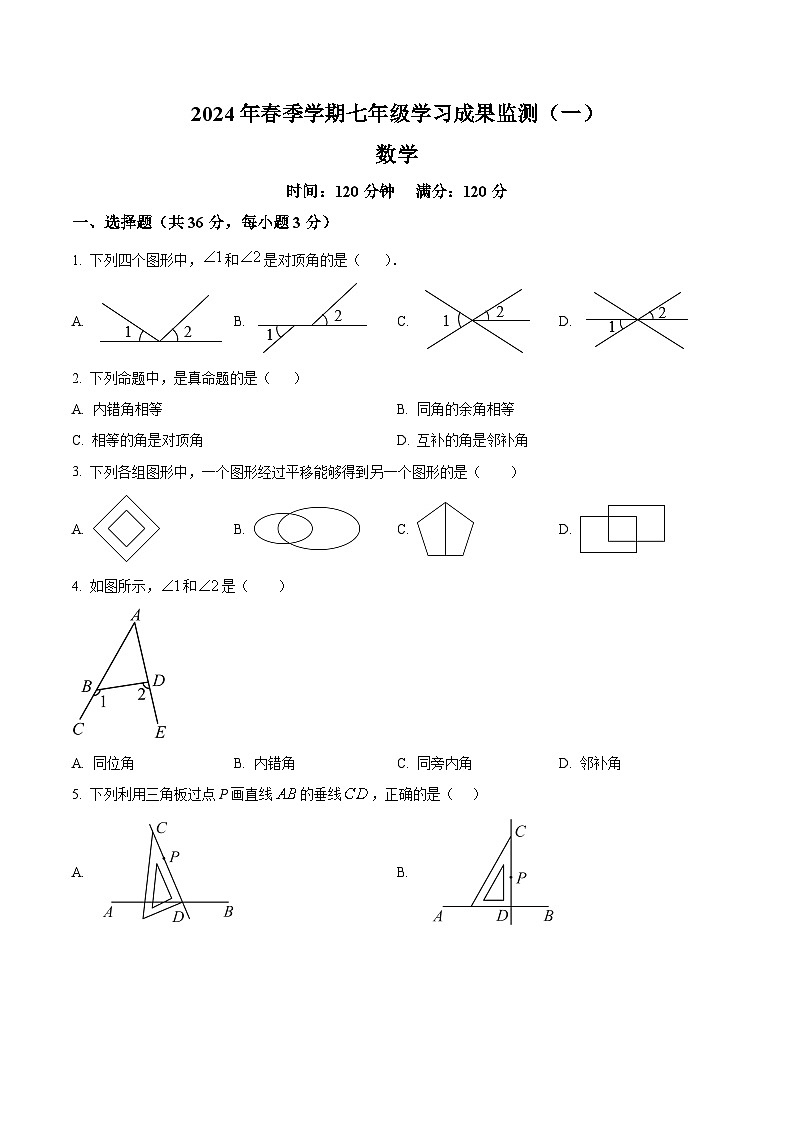
一、选择题（共36分，每小题3分）
1. 下列四个图形中，和是对顶角的是（ ）．
A. B. C. D.
【答案】D
【解析】
【分析】根据对顶角的定义，对顶角：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角，据此即可判断．
【详解】解： A、两角只有一条边互为反向延长线，另一条边没有互为反向延长线，不符合题意；
B、两角没有公共顶点，两角也是只有一条边互为反向延长线，另一条边没有互为反向延长线，不符合题意；
C、两角只有一条边互为反向延长线，另一条边没有互为反向延长线，不符合题意；
D、两角有一个公共顶点，并且一个角的两边是另一个角两边的反向延长线的两个角，符合题意；
故选：D．
【点睛】本题考查了对顶角的定义，属于基础题，熟练掌握对顶角的概念是解决本题的关键．
2. 下列命题中，是真命题的是（ ）
A. 内错角相等B. 同角的余角相等
C. 相等的角是对顶角D. 互补的角是邻补角
【答案】B
【解析】
【分析】考查了命题与定理以及内错角、同角的余角、对顶角、邻补角的定义和性质等知识，解题的关键是理解内错角、同角的余角、对顶角、邻补角的定义和性质．
根据真命题的定义及内错角、同角的余角、对顶角、邻补角的定义和性质逐项分析即可．
【详解】解：A．内错角不一定相等，故内错角相等是假命题，不符合题意；
B．同角的余角相等，是真命题，符合题意；
C．相等的角不一定是对顶角，故相等的角是对顶角是假命题，不符合题意；
D．互补的角不一定是邻补角，故互补的角是邻补角是假命题，不符合题意；
故选：B．
3. 下列各组图形中，一个图形经过平移能够得到另一个图形的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据平移的性质对各选项进行判断．
【详解】解：A．两正方形的大小不一样，所以A选项不符合题意；
B．两图形的大小不一样，所以B选项不符合题意；
C．左边的图形通过折叠可与右边的图形重合，所以C选项不符合题意；
D．一个矩形可以通过平移得到另一个矩形，所以D选项符合题意．
故选：D．
【点睛】此题考查了平移的性质，熟练掌握平移的有关性质是解题的关键．
4. 如图所示，和是（ ）

A. 同位角B. 内错角C. 同旁内角D. 邻补角
【答案】C
【解析】
【分析】本题主要考查了“三线八角”，解题的关键是熟练掌握同旁内角的定义，“两条直线被第三条直线所截，在截线同旁，且在被截线之内的两角，叫做同旁内角”．
【详解】解：由图可知，和是同旁内角，故C正确．
故选：C．
5. 下列利用三角板过点P画直线的垂线，正确的是（ ）
A B.
C. D.
【答案】B
【解析】
【分析】根据垂线的定义判断即可．
【详解】解：根据垂线的定义可知选项B中，直线经过点P，，符合题意．
故选：B．
【点睛】本题考查作图-简单作图，垂线的定义等知识，解题的关键是理解，垂线的定义．
6. 下列说法错误的是（ ）
A. 0.4的算术平方根是0.02B. 是16的一个平方根
C. 5是的算术平方根D. 的算术平方根是
【答案】A
【解析】
【分析】原式各项利用平方根、算术平方根定义判断即可．
【详解】解：A、∵，
∴0.4的算术平方根不是0.02，故选项A符合题意；
B、-4是16的一个平方根，正确，不符合题意；
C、5是的算术平方根，正确，不符合题意；
D、的算术平方根是，正确，不符合题意．
故选：A．
【点睛】此题考查了算术平方根，平方根，熟练掌握各自的定义是解本题的关键．
7. 一个数的相反数是最大的负整数，则这个数的平方根是（ ）
A. B. 1C. D. 0
【答案】C
【解析】
【分析】由于最大的负整数是-1，本题即求-1的相反数，进而求其平方根．
【详解】解：最大的负整数是-1，根据概念，（-1的相反数）+（-1）=0，
则-1的相反数是1，则这个数是1，1的平方根是，
故选：C．
【点睛】本题考查了相反数、负整数的概念及求一个数的平方根，正确掌握相关定义是解题的关键．
8. 下列化简结果正确的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】根据负的平方根、算术平方根和平方根的定义逐一判断即可．
【详解】解：A． ，故本选项符合题意；
B． ，故本选项不符合题意；
C． ，故本选项不符合题意；
D． ，故本选项不符合题意．
故选A．
【点睛】此题考查的是平方根的相关概念，掌握负的平方根、算术平方根和平方根的定义是解题关键．
9. 立方根为的数是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据解答即可，本题考查了立方根定义，熟练掌握定义是解题的关键．
【详解】∵，
∴故选：C．
10. 在实数，0，，3.14，，π 中，无理数有（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
【分析】根据无理数的定义，“无限不循环的小数是无理数”逐个分析判断即可．
【详解】解：在，0，，3.14，，π中，
，0，3.14是有理数，，，π是无理数，共3个，
故选C．
【点睛】本题考查了无理数，解答本题的关键掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有的数．
11. 下列说法错误的是（ ）
A. 平方根等于它本身的数只有0B. 绝对值最小的实数是零
C. 不带根号的数都是有理数D. 1的算术平方根是1
【答案】C
【解析】
【分析】根据平方根等于它本身的数只有0，绝对值最小的数是0，有理数的定义，算术平方根的定义，进行选择．
【详解】解：A、平方根等于它本身的数只有0，故不符合题意；
B、绝对值最小的实数是零，故不符合题意；
C、π不带根号，不是有理数，故符合题意；
D、1的算术平方根是1，故不符合题意．
故选：C．
【点睛】本题考查了实数，平方根，算术平方根，绝对值的性质，关键是熟悉几个特殊的数：0，1，．
12. 、、为同一平面内的三条直线，若与不平行，与不平行，那么下列判断正确的是（ ）
A. 与一定不平行B. 与一定平行
C. 与一定互相垂直D. 与可能相交或平行
【答案】D
【解析】
【分析】根据关键语句“若与不平行, 与不平行,”画出图形，图形有两种情况，根据图形可得答案．
【详解】根据题意可得图形：
根据图形可知：若与不平行,与不平行,则与可能相交或平行，
故选：D.
【点睛】本题主要考查了直线的位置关系，在同一平面内，两条直线的位置关系：平行或相交.
二、填空题（共12分，每空2分）
13. 的平方根是____．
【答案】±3
【解析】
【分析】根据算术平方根、平方根解决此题．
详解】解：，
实数的平方根是．
故答案为：．
【点睛】本题主要考查算术平方根、平方根，熟练掌握算术平方根、平方根是解题的关键．
14. 计算：______．
【答案】4
【解析】
【分析】由题意直接利用去绝对值法则和立方根性质进行运算即可得出答案.
【详解】解：，，
则.
故答案为：4.
【点睛】本题考查实数的运算，熟练掌握去绝对值法则和立方根性质是解题的关键.
15. 如图，所示，请添加一个条件，使．则添加的条件为___________．
【答案】（答案不唯一）
【解析】
【分析】本题主要考查了平行线的判定，熟知平行线的判定定理是解题的关键．
【详解】解：添加条件，理由如下：
∵，
∴（同位角相等，两直线平行），
故答案为；（答案不唯一）．
16. 如图，将两个含角的直角三角板的最长边靠在一起滑动，可知直角边，依据是______．
【答案】内错角相等，两直线平行
【解析】
【分析】图中的两个30°的角是一对内错角，而内错角相等，两直线平行，据此可得答案．
【详解】解：因为∠BAD=∠ADC=30°，
所以，理由是：内错角相等，两直线平行．
故答案为：内错角相等，两直线平行．
【点睛】本题考查了平行线的判定，属于基础题型，熟练掌握平行线的判定方法是关键．
17. 在实数、5.0101001中，无理数有__________个．
【答案】2
【解析】
【分析】无理数就是无限不循环小数，理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数，由此即可判定选择项．
本题主要考查了无理数的定义，其中初中范围内学习的无理数有：等；开方开不尽的数；以及像，等数．
【详解】解：
无理数有，
故答案为：2．
18. 比较大小：______（填“＞”、“＝”或“＜”）．
【答案】
【解析】
【分析】本题考查了实数的大小比较，掌握实数的大小比较的法则是解题关键．
根据，即可求解．
【详解】解：∵,
∴，
故答案为：＞．
三、解答题（共72分）
19. 计算题
（1）
（2）
【答案】（1）1 （2）
【解析】
【分析】（1）根据立方根定义及性质、算术平方根定义及性质化简后计算即可；
（2）根据立方根定义及性质和算术平方根的定义及性质化简后计算即可．
本题考查立方根定义及性质和算术平方根的定义及性质，熟练掌握相关定义及运算法则是解决问题的关键．
【小问1详解】
；
【小问2详解】
．
20. 把下列各数填入相应的大括号里．
，5，，，，，0，，，
正数： { … }
负数： { … }
有理数：{ … }
无理数：{ … }
【答案】正数： { 5，，，… }
负数： {，，，， }
有理数：{，5，，，，，0，… }
无理数：{， }
【解析】
【分析】根据正数、负数、有理数、无理数的定义分类即可.
【详解】正数： { 5，，，… }
负数： {，，，， }
有理数：{，5，，，，，0，… }
无理数：{， }
21. 如图，，，．将求的过程填写完整．
解：，（已知）
________．（ ）
又，（已知）
________．（ ）
________．（ ）
________．
又，（已知）
________．
【答案】；两直线平行，同位角相等；；等量代换；；内错角相等，两直线平行；；
【解析】
【分析】本题主要考查了平行线的判定和性质，解题的关键是熟练掌握平行线的判定定理和性质定理．根据平行线的性质得出，根据，得出，根据平行线的判定得出，根据平行线的性质得出，最后求出结果即可．
【详解】解：，（已知）
．（两直线平行，同位角相等）
又，（已知）
．（等量代换）
．（内错角相等，两直线平行）
．
又，（已知）
．
故答案为：；两直线平行，同位角相等；；等量代换；；内错角相等，两直线平行；；．
22. 已知△ABC中，CD平分∠ACB，∠2=∠3，∠B=70° 求∠1的度数．
【答案】∠1=70°
【解析】
【分析】根据CD平分∠ACB，∠2=∠3，可得到∠BCD=∠2，从而DE//BC，即可解答．
【详解】解：∵CD平分∠ACB
∴∠BCD=∠3
∵∠2=∠3
∴∠BCD=∠2
∴DE//BC
∴∠1=∠B
又∵∠B=70°
∴∠1=70°．
故答案为：∠1=70°
【点睛】本题主要考查了平行线的判定和性质，角平分线的定义，解题的关键是熟练掌握平行线的判定定理和性质定理．
23. 已知实数x，y满足．
（1）求x，y的值；
（2）求的平方根．
【答案】（1），
（2）
【解析】
【分析】（1）根据非负数的性质列式，即可求出x、y的值，
（2）根据（1）求得的x、y的值，代入代数式进行计算即可得解．
【小问1详解】
由题意得：，，
解得：，
【小问2详解】
由（1）得：，，
∴，
∴的平方根
【点睛】本题主要考查了非负数的性质，即算术平方根和绝对值的性质．解题的关键是根据非负数的性质求得x，y的值．
24. 如图，直线与相交于点，为射线．
（1）写出的对顶角．
（2）写出邻补角．
（3）若，求和的度数．
【答案】（1）
（2）
（3），
【解析】
【分析】本题主要考查对顶角、邻补角的定义，角的和差计算，理解定义，图形结合是解题的关键．
（1）根据对顶角的定义，图形结合即可求解；
（2）根据邻补角的定义，图形结合即可求解；
（3）根据题意可得，，由此可求出的度数，根据邻补角可求出的度数，再根据即可求解．
【小问1详解】
解：的对顶角是．
【小问2详解】
解：的邻补角．
【小问3详解】
解：∵，，且，
∴，
∵，
∴，
∵．
25. 如图，，，．

（1）求的度数；
（2）如果是的平分线，那么与平行吗？请说明理由．
【答案】（1）60° （2），证明见解析
【解析】
分析】（1）根据平行线的性质和已知求出，即可得出答案；
（2）求出，根据平行线的性质求出，求出，即可得出，根据平行线的判定得出即可．
【小问1详解】
解：∵，
∴，
∵，，
∴；
【小问2详解】
解：，
理由是：∵，，
∴，
∵，，
∴，
∵平分，
∴，
∴，
∴．
【点睛】本题考查了平行线的性质和判定的应用，能综合运用定理进行推理是解此题的关键．
26. 我们知道，负数没有算术平方根，但对于三个互不相等的负整数，若两两乘积的算术平方根都是整数，则称这三个数为“完美组合数”，例如： ，， 这三个数，，，其结果 6，3，2 都是整数，所以，，这三个数称为“完美组合数”，请问：，， 这三个数是“完美组合数”吗? 请说明理由
【答案】是，理由见解析
【解析】
【分析】根据定义计算判断，本题考查了新定义，正确理解定义是解题的关键.
【详解】，，这三个数是“完美组合数”，理由如下
，，，
其结果 12，4，6 都是整数，
∴，，这三个数称为“完美组合数”.