数学苏科版6.3 相似图形练习题

这是一份数学苏科版6.3 相似图形练习题，共30页。试卷主要包含了单选，填空，解答题等内容，欢迎下载使用。
1 .如图，将图形用放大镜放大，应该属于（ ）．
A.平移变换
B.相似变换
C.旋转变换
D.对称变换
2 .如果两个相似多边形面积的比为，则它们的相似比为（ ）．
A.
B.
C.
D.
3 .如果两个相似多边形的面积比为，那么它们的周长比为（ ）．
A.
B.
C.
D.
4 .如图，将菱形沿方向平移得到菱形，若 ，菱形与菱形的重叠部分面积记为 ，菱形的面积记为，则的值为（ ）．
A.
B.
C.
D.
5 .如图，正方形中，内部有个全等的正方形，小正方形的顶点、、、分别在边、、、上，则( )
A.
B.
C.
D.
二、填空
1 .下列命题中，正确命题的个数为 ．
①所有的正方形都相似
②所有的菱形都相似
③边长相等的两个菱形相似
④对角线相等的两个矩形相似
2 .如图，菱形的对角线，把它沿对角线方向平移得到菱形．则图中阴影部分图形的面积与四边形的面积之比为 ．
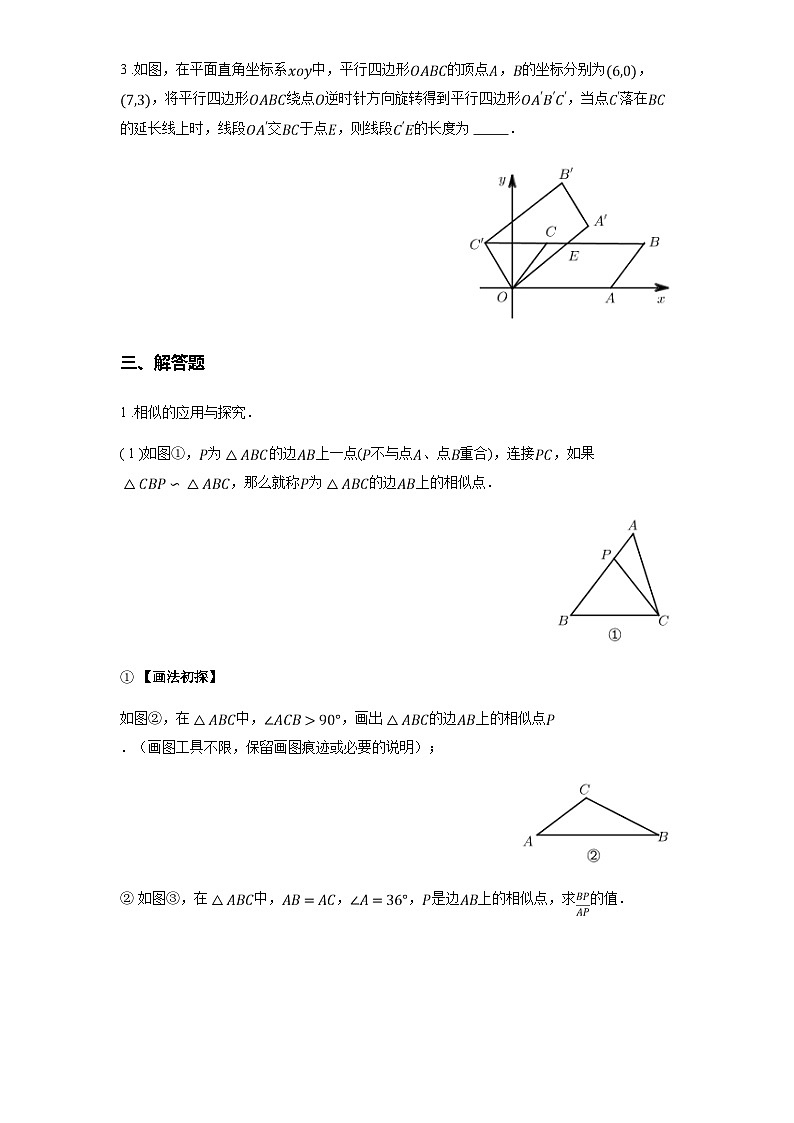
3 .如图，在平面直角坐标系中，平行四边形的顶点，的坐标分别为，，将平行四边形绕点逆时针方向旋转得到平行四边形，当点落在的延长线上时，线段交于点，则线段的长度为 ．
三、解答题
1 .相似的应用与探究．
( 1 )如图①，为的边上一点(不与点、点重合)，连接，如果，那么就称为的边上的相似点．
① 【画法初探】
如图②，在中，，画出的边上的相似点．（画图工具不限，保留画图痕迹或必要的说明）；
② 如图③，在中，，，是边上的相似点，求的值．
③ 【辩证思考】
是不是所有的三角形都存在它的边上的相似点？如果是，请说明理由；如果不是请找出一个不存在边上相似点的三角形．
④ 【特例分析】
已知为的边上的相似点连接，若，则的形状是 ．
( 2 )在矩形中，，，是上的点（不与点、点重合），作，垂足为．如果矩形矩形，那么就称为矩形的边、上的相似线．
① 类比()中的“ 画法初探”，可以提出问题：对于如图④的矩形，在不限制画图工具的前提下，如何画出它的边、上的相似线呢？
你的解答是： ．(只需描述的画法，不需在图上画出)
② 请继续类比()中的“ 辩证思考”、“ 特例分析”两个栏目对矩形的相似线进行研究，要求每个栏目提出一个问题并解决．
2 .如果两个多边形不仅相似（相似比不等于），而且有一条公共边，那么就称这两个多边形是共边相似多边形．例如，图①中，与是共边相似三角形，图②中，平行四边形与平行四边形是共边相似四边形．

( 1 )判断下列命题的真假（在相应括号内填上“真”或“假”）：
① 正三角形的共边相似三角形是正三角形．
② 如果两个三角形是位似三角形，那么这两个三角形不可能是共边相似三角形．
( 2 )如图③，在中，，，画个不全等的三角形，使这个三角形均是与共边的相似三角形．（要求：画图工具不限，不写画法，保留画图痕迹或有必要的说明）
( 3 )图④是相邻两边长分别为、（）的矩形，图⑤是边长为的菱形，图⑥是两底长分别为、，腰长为（）的等腰梯形，判断这三个图形是否存在共边相似四边形？如果存在，直接写出它们的共边相似四边形各边的长度．
( 4 )根据（）、（）和（）中获得的经验回答：如果一个多边形存在它的共边相似多边形，那么它必须满足条件： ．
3 .如图，在梯形中，，，，，，为线段上的一动点，且和、不重合，连接，过作交所在直线于．设，．
( 1 )求与的函数关系式．
( 2 )若点在线段上运动时，点总在线段上，求的取值范围．
( 3 )如图，若，将沿翻折至位置，，求长．
4 .下框中是小明对一道题目的解答以及老师的批改．
我的结果也正确！
小明发现他解答的结果是正确的，但是老师却在他的解答中画了一条横线，并打了一个“？”．
结果为何正确呢？
( 1 )请指出小明解答中存在的问题，并补充缺少的过程：
变化一下会怎样……
( 2 )如图，矩形在矩形的内部，，，且，设与、与、与、与之间的距离分别为、、、，要使矩形矩形，、、、应满足什么条件？请说明理由．
5 .如图，为的边上一点(不与点、点重合)，连接，如果，那么就称为的边上的相似点．
( 1 )如图，在中，，画出的边上的相似点．
（画图工具不限，保留画图痕迹或必要的说明）．
( 2 )是不是所有的三角形都存在它的边上的相似点如果是，请说明理由；如果不是，请找出一个不存在边上相似点的三角形 ．
( 3 )已知为的边上的相似点，连接，若，则的形状是 ．
( 4 )如图，在中，，，是边上的相似点，求的值．
6 .如图①，矩形中，，，点是边上一定点，且．
( 1 )当时，上存在点，使与相似，求的长度．
( 2 )如图②，当时，用直尺和圆规在上作出所有使与相似的点．
（不写作法，保留作图痕迹）
( 3 )对于每一个确定的值，边上存在几个点，使得与相似？
7 .对于两个相似三角形，如果沿周界按对应点顺序环绕的方向相同，那么称这两个三角形互为顺相似；如果沿周界按对应点顺序环绕的方向相反，那么称这两个三角形互为逆相似．例如，如图①，且沿周界与环绕的方向相同，因此与互为顺相似；如图②，，且沿周界与环绕的方向相反，因此与互为逆相似．
( 1 )根据图 I、图 II和图 III满足的条件，可得下列三对相似三角形：①与；②与；③与．其中，互为顺相似的是 ；互为逆相似的是 ．（填写所有符合要求的序号）
( 2 )如图③，在锐角中，，点在的边上（不与点、、重合）．过点画直线截，使截得的一个三角形与互为逆相似．请根据点的不同位置，探索过点的截线的情形，画出图形并说明截线满足的条件，不必说明理由．
6.3 相似图形练习
一、单选
1 .如图，将图形用放大镜放大，应该属于（ ）．
A.平移变换
B.相似变换
C.旋转变换
D.对称变换
【答案】 B
【解析】 根据相似图形的定义知，用放大镜将图形放大，属于图形的形状相同，大小不相同，所以属于相似变换．
故选．
2 .如果两个相似多边形面积的比为，则它们的相似比为（ ）．
A.
B.
C.
D.
【答案】 D
【解析】 ∵两个相似多边形面积的比为．
∴它们的相似比为．
3 .如果两个相似多边形的面积比为，那么它们的周长比为（ ）．
A.
B.
C.
D.
【答案】 B
【解析】 相似比等于周长比，面积比等于相似比的平方，
所以面积比等于周长比的平方，
因为面积比为，
故周长比为．
故选：．
4 .如图，将菱形沿方向平移得到菱形，若 ，菱形与菱形的重叠部分面积记为 ，菱形的面积记为，则的值为（ ）．
A.
B.
C.
D.
【答案】 D
【解析】 由知．
即菱形与菱形的重叠部分与菱形的相似比为，故面积比等于相似比的平分，
即，故选.
5 .如图，正方形中，内部有个全等的正方形，小正方形的顶点、、、分别在边、、、上，则( )
A.
B.
C.
D.
【答案】 A
【解析】 解：如图所示：
设正方形边长为，
，，
过点作，垂足为，
则，
四边形是矩形，
，，
个全等的小正方形如图放置在大正方形中，
，
，
，
，
，
，
，
同理，
，
同理可证：，
，
；
故选：A．
二、填空
1 .下列命题中，正确命题的个数为 ．
①所有的正方形都相似
②所有的菱形都相似
③边长相等的两个菱形相似
④对角线相等的两个矩形相似
【答案】 个
【解析】 两个形状相同的图形相似，所有正方形形状相同，因此相似，①正确；
菱形四边相等，但是角不一定对应相等，②错误；
边长相等的菱形，角不一定对应相等，③错误；
对角线相等的矩形不一定相似，长宽比相等的矩形才相似，④错误．
因此只有①正确，正确的个数为个．
故答案为：个．
2 .如图，菱形的对角线，把它沿对角线方向平移得到菱形．则图中阴影部分图形的面积与四边形的面积之比为 ．
【答案】
【解析】 由平移的性质可知，//，，
所以，
，
，
故可设， ，
，
，
所以图中阴影部分的面积与四边形的面积之比为．
故本题答案为．
3 .如图，在平面直角坐标系中，平行四边形的顶点，的坐标分别为，，将平行四边形绕点逆时针方向旋转得到平行四边形，当点落在的延长线上时，线段交于点，则线段的长度为 ．
【答案】
【解析】 ∵四边形为平行四边形，
∴，，
∵，，
∴，
∵，轴，
∴关于轴对称，
∴，
∵旋转，
∴，
∴，
∵，
∴，
∴，
∵，
∴，
∴，
设，
∴，
∴，
∴．
三、解答题
1 .相似的应用与探究．
( 1 )如图①，为的边上一点(不与点、点重合)，连接，如果，那么就称为的边上的相似点．
① 【画法初探】
如图②，在中，，画出的边上的相似点．（画图工具不限，保留画图痕迹或必要的说明）；
② 如图③，在中，，，是边上的相似点，求的值．
③ 【辩证思考】
是不是所有的三角形都存在它的边上的相似点？如果是，请说明理由；如果不是请找出一个不存在边上相似点的三角形．
④ 【特例分析】
已知为的边上的相似点连接，若，则的形状是 ．
( 2 )在矩形中，，，是上的点（不与点、点重合），作，垂足为．如果矩形矩形，那么就称为矩形的边、上的相似线．
① 类比()中的“ 画法初探”，可以提出问题：对于如图④的矩形，在不限制画图工具的前提下，如何画出它的边、上的相似线呢？
你的解答是： ．(只需描述的画法，不需在图上画出)
② 请继续类比()中的“ 辩证思考”、“ 特例分析”两个栏目对矩形的相似线进行研究，要求每个栏目提出一个问题并解决．
【答案】 (1)①画图见解析．
②．
③不是，如正三角形．
④直角三角形
(2)①连接，过作交于点，过作
② 辩证思考
问题：是不是所有的矩形都存在它的边上的相线？如果是，请说明理由；如
果不是，请找出一个不存在边上相似线的矩形
解答：不是，如正方形
特例分析
答案不唯一，以下答案供参考
)问题：已知为矩形的边、上的相似线，且
矩形矩形，、之间有何数量关系？
解答：
)问题：已知为矩形的边、上的相似线，且是的中点
、之间有何数量关系？
解答：
)问题：已知为矩形的边、上的相似线，当，时
求．
解答：．
)问题：已知矩形为黄金矩形(即)，为矩形的边
、上的相似线，求．
解答：．
【解析】 (1)①作图，过点作，交边于点，则点即为所求．
②设，
∵，，
，
，
，
，
，
∵，
∴，
∴，解得，（舍去）
∴．
③略．
④略．
(2)①
②略．
2 .如果两个多边形不仅相似（相似比不等于），而且有一条公共边，那么就称这两个多边形是共边相似多边形．例如，图①中，与是共边相似三角形，图②中，平行四边形与平行四边形是共边相似四边形．

( 1 )判断下列命题的真假（在相应括号内填上“真”或“假”）：
① 正三角形的共边相似三角形是正三角形．
② 如果两个三角形是位似三角形，那么这两个三角形不可能是共边相似三角形．
( 2 )如图③，在中，，，画个不全等的三角形，使这个三角形均是与共边的相似三角形．（要求：画图工具不限，不写画法，保留画图痕迹或有必要的说明）
( 3 )图④是相邻两边长分别为、（）的矩形，图⑤是边长为的菱形，图⑥是两底长分别为、，腰长为（）的等腰梯形，判断这三个图形是否存在共边相似四边形？如果存在，直接写出它们的共边相似四边形各边的长度．
( 4 )根据（）、（）和（）中获得的经验回答：如果一个多边形存在它的共边相似多边形，那么它必须满足条件： ．
【答案】 (1)①假
②真
(2)画图见解析．
(3)该矩形存在共边相似四边形，各边长有两种情况，
分别是：①，，，；②，，，．
该菱形不存在共边相似四边形．
该等腰梯形存在共边相似四边形，各边长有六种情况，
分别是：①，，，；②，，，；③，，，；④，，，；⑤，，，；⑥，，，．
(4)至少有两条边不相等，或各边长度不全相等（答案不唯一）
【解析】 (1)①共边的两个等边三角形相似，相似比为，故此命题为：假．
②此命题为真，因为若两个位似图形为共边相似图形，则相似比为．
(2)如图，．
(3)该矩形存在共边相似四边形，各边长有两种情况，
分别是：①，，，；②，，，．
该菱形不存在共边相似四边形．
该等腰梯形存在共边相似四边形，各边长有六种情况，
分别是：①，，，；②，，，；③，，，；④，，，；⑤，，，；⑥，，，．
(4)表述方法不唯一，如至少有两条边不相等，或各边长度不全相等，等等．
3 .如图，在梯形中，，，，，，为线段上的一动点，且和、不重合，连接，过作交所在直线于．设，．
( 1 )求与的函数关系式．
( 2 )若点在线段上运动时，点总在线段上，求的取值范围．
( 3 )如图，若，将沿翻折至位置，，求长．
【答案】 (1)．
(2)
(3)或．
【解析】 (1)．
(2)．
(3)分别延长、交于点，
易证四边形是矩形，
由翻折及，可得，
进而得到．
故，
所以，
在中，，，，
由勾股定理得：，
整理得：，
由（）中，
其中，可得
解得：，，
故长为或．
连接交于，
易知为中点，，
∴，为平行四边形．
设，
∴，，．
∵，
∴．
，
解得，．
4 .下框中是小明对一道题目的解答以及老师的批改．
我的结果也正确！
小明发现他解答的结果是正确的，但是老师却在他的解答中画了一条横线，并打了一个“？”．
结果为何正确呢？
( 1 )请指出小明解答中存在的问题，并补充缺少的过程：
变化一下会怎样……
( 2 )如图，矩形在矩形的内部，，，且，设与、与、与、与之间的距离分别为、、、，要使矩形矩形，、、、应满足什么条件？请说明理由．
【答案】 (1)证明见解析．
(2)．
【解析】 (1)小明没有说明矩形蔬菜种植区域的长与宽之比为的理由．
在“设矩形蔬菜种植区域的宽为，则长为．”前补充以下过程：
设温室的宽为，则长为．
则矩形蔬菜种植区域的宽为，长为．
∵，
∴矩形蔬菜种植区域的长与宽之比为．
(2)要使矩形矩形，
则，即，
即，
即，
∴，
即．
5 .如图，为的边上一点(不与点、点重合)，连接，如果，那么就称为的边上的相似点．
( 1 )如图，在中，，画出的边上的相似点．
（画图工具不限，保留画图痕迹或必要的说明）．
( 2 )是不是所有的三角形都存在它的边上的相似点如果是，请说明理由；如果不是，请找出一个不存在边上相似点的三角形 ．
( 3 )已知为的边上的相似点，连接，若，则的形状是 ．
( 4 )如图，在中，，，是边上的相似点，求的值．
【答案】 (1)画图见解析．
(2)不是，如正三角形．
(3)直角三角形
(4)．
【解析】 (1)
(2)不是，当三角形为正三角形时，如果，此时点与、重合，与题意矛盾，此时不存在相似点．
(3)因为，，
所以，
所以三角形形状为直角三角形．
(4)设，，
∵，，
，
，
，
，
，
,
,
，
解得，（舍去）．
．
6 .如图①，矩形中，，，点是边上一定点，且．
( 1 )当时，上存在点，使与相似，求的长度．
( 2 )如图②，当时，用直尺和圆规在上作出所有使与相似的点．
（不写作法，保留作图痕迹）
( 3 )对于每一个确定的值，边上存在几个点，使得与相似？
【答案】 (1)或．
(2)画图见解析．
(3)①当且时，有个点；
②当或时，有个点；
③当时，有个点．
【解析】 (1)存在．设，
①当时，
，
，
．
解得，．
∴或．
②当时，
，
，
解得．
(2)
如图，、和即为所求．
(3)，，
①当，
，
，
解得：．
②当，
，
，
，
．
若，无点；
若，有个点；
若，有个点．
而当时，①②两种情况会有重合的点．
综上：①当且时，有个点；
②当或时，有个点；
③当时，有个点．
7 .对于两个相似三角形，如果沿周界按对应点顺序环绕的方向相同，那么称这两个三角形互为顺相似；如果沿周界按对应点顺序环绕的方向相反，那么称这两个三角形互为逆相似．例如，如图①，且沿周界与环绕的方向相同，因此与互为顺相似；如图②，，且沿周界与环绕的方向相反，因此与互为逆相似．
( 1 )根据图 I、图 II和图 III满足的条件，可得下列三对相似三角形：①与；②与；③与．其中，互为顺相似的是 ；互为逆相似的是 ．（填写所有符合要求的序号）
( 2 )如图③，在锐角中，，点在的边上（不与点、、重合）．过点画直线截，使截得的一个三角形与互为逆相似．请根据点的不同位置，探索过点的截线的情形，画出图形并说明截线满足的条件，不必说明理由．
【答案】 (1)①②③
(2)证明见解析．
【解析】 (1)①②；③．
(2)根据点在边上的位置分为以下三种情况．
第一种情况：如图①，点在（不含点、）上，过点只能画出条截线、，分别使，，此时、都与互为逆相似．
第二种情况：如图②，点在（不含点、）上，过点作，交于点．
当点在（不含点）上时，过点只能画出条截线，使，此时与互为逆相似；
当点在上时，过点只能画出条截线、，分别使，，此时、都与互为逆相似．
第三种情况：如图③，点在（不含点、）上，过点作，，、分别交于点、．
当点在（不含点）上时，过点只能画出条截线，使，此时与互为逆相似；
当点在上时，过点只能画出条截线、，分别使，，此时、都与互为逆相似；
当点在（不含点）上时，过点只能画出条截线，使，此时与互为逆相似．
题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为，在温室内，沿前侧内墙保留的空地，其他三侧内墙各保留的通道，当温室的长与宽各为多少时，矩形蔬菜种植区域的面积是？
解： 设矩形蔬菜种植区域的宽为，则长为
根据题意，得．
解这个方程，得（不合题意，舍去），，
所以温室的长为（），宽为（）．
答：当温室的长为，宽为时，矩形蔬菜种植区域的面积是．
题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为，在温室内，沿前侧内墙保留的空地，其他三侧内墙各保留的通道，当温室的长与宽各为多少时，矩形蔬菜种植区域的面积是？
解： 设矩形蔬菜种植区域的宽为，则长为
根据题意，得．
解这个方程，得（不合题意，舍去），，
所以温室的长为（），宽为（）．
答：当温室的长为，宽为时，矩形蔬菜种植区域的面积是．