2024年山东省泰安市新泰实验中学中考数学模拟试卷（3月份）（含解析）

这是一份2024年山东省泰安市新泰实验中学中考数学模拟试卷（3月份）（含解析），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列式子中，为最简二次根式的是( )
A. 12B. 2C. 4D. 12
2.遵义市2019年6月1日的最高气温是25℃，最低气温是15℃，遵义市这一天的最高气温比最低气温高( )
A. 25℃B. 15℃C. 10℃D. −10℃
3.下列长度的三条线段，能组成三角形的是( )
A. 2，2，4B. 5，6，12C. 6，8，10D. 5，7，2
4.如图所示，直线l1：y=32x+6与直线l2：y=−52x−2交于点P(−2,3)，不等式32x+6>−52x−2的解集是( )
A. x>−2
B. x≥−2
C. x<−2
D. x≤−2
5.某书店拿取高处书籍的登高梯如图位置摆放，登高梯AC的顶端A恰好放在书架的第七层的顶端.已知登高梯的长度AC为3米，登高梯与地面的夹角∠ACB为72°，则书架第七层顶端离地面的高度AB为( )
A. 3sin72°米B. 3sin72∘米C. 3cs72°米D. 3cs72∘米
6.将一副三角尺按如图摆放，点E在AC上，点D在BC的延长线上，EF/​/BC，∠B=∠EDF=90°，∠A=45°，∠F=60°，则∠CED的度数是( )
A. 15°B. 20°C. 25°D. 30°
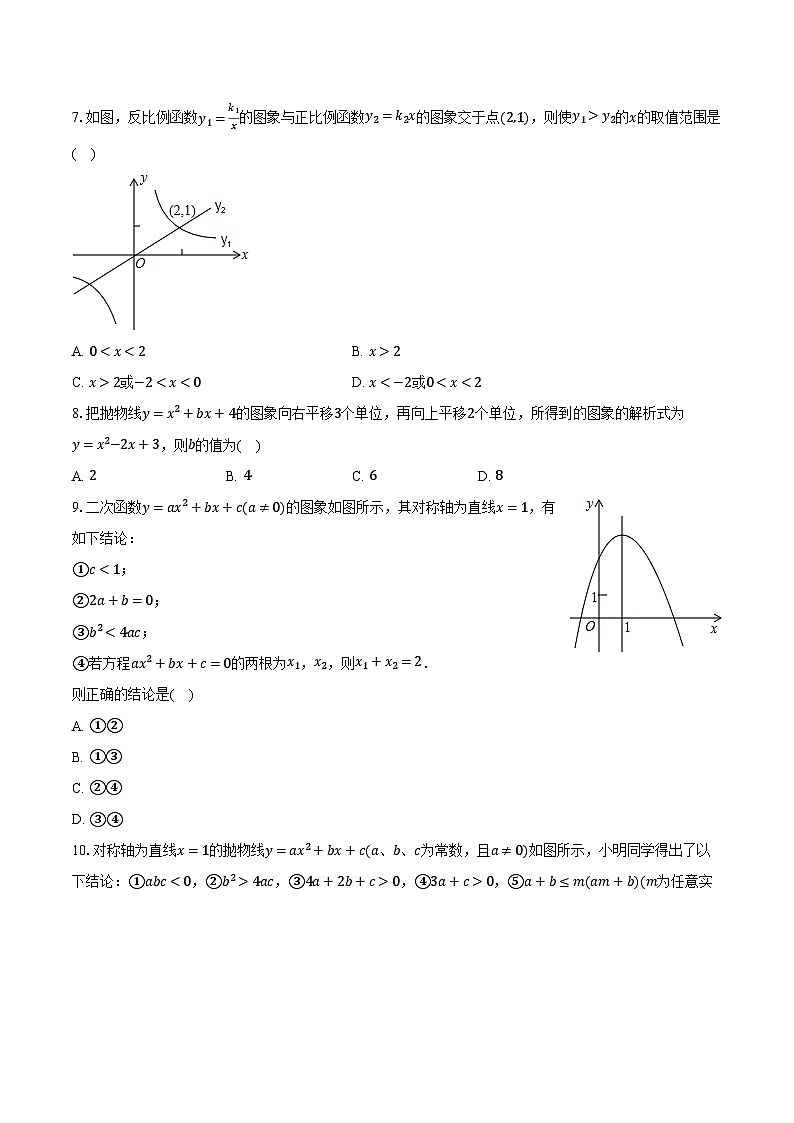
7.如图，反比例函数y1=k1x的图象与正比例函数y2=k2x的图象交于点(2,1)，则使y1>y2的x的取值范围是( )
A. 02
C. x>2或−28.把抛物线y=x2+bx+4的图象向右平移3个单位，再向上平移2个单位，所得到的图象的解析式为y=x2−2x+3，则b的值为( )
A. 2B. 4C. 6D. 8
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示，其对称轴为直线x=1，有如下结论：
①c<1；
②2a+b=0；
③b2<4ac；
④若方程ax2+bx+c=0的两根为x1，x2，则x1+x2=2．
则正确的结论是( )
A. ①②
B. ①③
C. ②④
D. ③④
10.对称轴为直线x=1的抛物线y=ax2+bx+c(a、b、c为常数，且a≠0)如图所示，小明同学得出了以下结论：①abc<0，②b2>4ac，③4a+2b+c>0，④3a+c>0，⑤a+b≤m(am+b)(m为任意实数)，⑥当x<−1时，y随x的增大而增大．其中结论正确的个数为( )
A. 3B. 4C. 5D. 6
二、填空题：本题共6小题，每小题3分，共18分。
11.如图，已知四边形ABCD内接于⊙O，∠ABC=68°，则∠ADC的度数是______．
12.《孙于算经》是中国古代重要的数学著作，其中一道题的原文是：“今三人共车，两车空；二人共车，九人步，问人与车各几何？”意思是：现有若干人和车，若每辆车乘坐3人，则空余两辆车；若每辆车乘坐2人，则有9人步行，问人与车各多少？设有x人，y辆车，可列方程组为______．
13.如图，在矩形纸片ABCD中，AB=2，AD=3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的长的最小值是______．
14.如图，已知第一象限内的点A在反比例函数y=2x的图象上，第二象限的点B在反比例函数y=kx的图象上，且OA⊥OB，tan∠BAO=2，则k的值为______．
15.如图，在⊙O内有一个平行四边形OABC，点A，B，C在圆上，点N为边AB上一动点(点N与点B不重合)，⊙O的半径为1，则阴影部分面积为______．
16.如图所示，将形状大小完全相同的“▱”按照一定规律摆成下列图形.第1幅图中“▱”的个数为a1，第2幅图中“▱”的个数为a2，第3幅图中“▱”的个数为a3，以此类推，2a1+2a2+2a3+⋯+2a2023的值为______．
三、解答题：本题共8小题，共64分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题6分)
化简求值：(x−1x−x−2x+1)÷2x−1x(x+2)+x+2，其中x= 3．
18.(本小题8分)
疫情期间，我市积极开展“停课不停学”线上教学活动，并通过电视、手机APP等平台进行教学视频推送．某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为：A.效果很好；B.效果较好；C.效果一般；D.效果不理想)，并根据调查结果绘制了如图两幅不完整的统计图：
(1)此次调查中，共抽查了______名学生；
(2)补全条形统计图，并求出扇形统计图中∠α的度数；
(3)某班4人学习小组，甲、乙2人认为效果很好，丙认为效果较好，丁认为效果一般．从学习小组中随机抽取2人，则“1人认为效果很好，1人认为效果较好”的概率是多少？(要求画树状图或列表求概率)
19.(本小题8分)
图1是某小区入口实景图，图2是该入口抽象成的平面示意图．已知入口BC宽3.9米，门卫室外墙AB上的O点处装有一盏路灯，点O与地面BC的距离为3.3米，灯臂OM长为1.2米(灯罩长度忽略不计)，∠AOM=60°．
(1)求点M到地面的距离；
(2)某搬家公司一辆总宽2.55米，总高3.5米的货车从该入口进入时，货车需与护栏CD保持0.65米的安全距离，此时，货车能否安全通过？若能，请通过计算说明；若不能，请说明理由．(参考数据： 3≈1.73，结果精确到0.01米)
20.(本小题10分)
某超市采购了两批同样的冰墩墩挂件，第一批花了6600元，第二批花了8000元，第一批每个挂件的进价是第二批的1.1倍，且第二批比第一批多购进50个．
(1)求第二批每个挂件的进价；
(2)两批挂件售完后，该超市以第二批每个挂件的进价又采购一批同样的挂件，经市场调查发现，当售价为每个60元时，每周能卖出40个，若每降价1元，每周多卖10个，由于货源紧缺，每周最多能卖90个，求每个挂件售价定为多少元时，每周可获得最大利润，最大利润是多少？
21.(本小题8分)
如图，在平面直角坐标系中，四边形ABCD是平行四边形，点A，B，C的坐标分别为A(1,0)，B(3,1)，C(3,3).反比例函数y=kx(x>0)的函数图象经过点D，点P是反比例函数上一动点，直线PC的解析式为：y=ax+b(a≠0)．
(1)求反比例函数的解析式；
(2)对于一次函数y=ax+b(a≠0)，当y随x的增大而增大时，直接写出点P的横坐标x的取值范围．
22.(本小题8分)
如图，正方形ABCD中，AB=2 5，O是BC边的中点，点E是正方形内一动点，OE=2，连接DE，将线段DE绕点D逆时针旋转90°得DF，连接AE，CF．
(1)求证：AE=CF；
(2)若A，E，O三点共线，连接OF，求线段OF的长．
(3)求线段OF长的最小值．
23.(本小题8分)
在平面直角坐标系xOy中，已知抛物线y=ax2+bx+c与x轴交于A(−1,0)，B(4,0)两点，与y轴交于点C(0,−2)．
(1)求抛物线的函数表达式；
(2)如图1，点D为第四象限抛物线上一点，连接AD，BC交于点E，连接BD，记△BDE的面积为S1，△ABE的面积为S2，求S1S2的最大值；
(3)如图2，连接AC，BC，过点O作直线l/​/BC，点P，Q分别为直线l和抛物线上的点．试探究：在第一象限是否存在这样的点P，Q，使△PQB∽△CAB.若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．
24.(本小题8分)
已知△ABC内接于⊙O，∠BAC的平分线交⊙O于点D，连接DB，DC．
(1)如图①，当∠BAC=120°时，请直接写出线段AB，AC，AD之间满足的等量关系式：______；
(2)如图②，当∠BAC=90°时，试探究线段AB，AC，AD之间满足的等量关系，并证明你的结论；
(3)如图③，若BC=5，BD=4，求ADAB+AC的值．
答案和解析
1.【答案】B
【解析】解：A、原式= 22，不符合题意；
B、是最简二次根式，符合题意；
C、原式=2，不符合题意；
D、原式=2 3，不符合题意；
故选：B．
利用最简二次根式定义判断即可．
此题考查了最简二次根式，熟练掌握最简二次根式是解本题的关键．
2.【答案】C
【解析】【分析】
本题主要考查有理数的减法，用最高气温减去最低气温即可．
【解答】
解：25−15=10(℃)．
故选C．
3.【答案】C
【解析】解：A、2+2=4，不能够组成三角形；
B、5+6<12，不能构成三角形；
C、6+8=14>10，能构成三角形；
D、5+2=7，不能构成三角形．
故选：C．
根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析．
此题主要考查了三角形三边关系，根据第三边的范围是：大于已知的两边的差，而小于两边的和是解决问题的关键．
4.【答案】A
【解析】解：由图象可知：当x>−2时，直线l1：y=32x+6在直线l2：y=−52x−2的上方，
即32x+6>−52x−2，
所以不等式32x+6>−52x−2的解集是x>−2．
故选：A．
利用函数图象写出直线l1：y=32x+6与在直线l2：y=−52x−2上方所对应的自变量的范围即可．
本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合．
5.【答案】A
【解析】解：由题意可得，
∠ABC=90°，AC=3米，∠ACB=72°，
∵sin∠ACB=ABAC，
∴AB=AC⋅sin∠ACB=3⋅sin72°(米)，
故选：A．
根据题目中的数据和锐角三角函数，可以计算出书架第七层顶端离地面的高度AB．
本题考查解直角三角形的应用—坡度坡角问题，解答本题的关键是明确题意，利用数形结合的思想解答．
6.【答案】A
【解析】【分析】
本题考查了三角形的内角和定理，平行线的性质，以及三角形的外角性质，牢记“两直线平行，内错角相等”是解题的关键．
根据三角形的内角和定理，得∠ACB=45°，∠DEF=30°，根据EF/​/BC可得∠BDE=∠DEF=30°，根据三角形的外角性质得∠ACB=∠BDE+∠CED，进而可得答案．
【解答】
解：∵∠B=90°，∠A=45°，
∴∠ACB=45°．
∵∠EDF=90°，∠F=60°，
∴∠DEF=30°．
∵EF/​/BC，
∴∠BDE=∠DEF=30°，
∵∠ACB=∠BDE+∠CED，
∴∠CED=∠ACB−∠BDE=45°−30°=15°．
故选A．
7.【答案】D
【解析】【分析】
先根据反比例函数与正比例函数的性质求出B点坐标，由函数图象即可得出结论．
本题考查的是反比例函数与一次函数的交点问题，能根据数形结合求出y1>y2时x的取值范围是解答此题的关键．
【解答】
解：∵反比例函数与正比例函数的图象均关于原点对称，
∴A、B两点关于原点对称，
∵A(2,1)，
∴B(−2,−1)，
∵由函数图象可知，当0∴使y1>y2的x的取值范围是x<−2或0故选D．
8.【答案】B
【解析】解：∵y=x2−2x+3=x2−2x+1+2=(x−1)2+2，
∴顶点坐标为(1,2)，
∴向左平移3个单位，再向下平移2个单位，得(−2,0)，
则原抛物线y=x2+bx+4的顶点坐标为(−2,0)，
∴原抛物线y=x2+bx+4=(x+2)2=x2+4x+4，
∴b=4．
故选：B．
首先根据点的坐标平移规律是上加下减，左加右减，利用这个规律即可得到所求抛物线的顶点坐标，然后就可以求出抛物线的解析式．
此题主要考查了平移规律，首先根据平移规律求出已知抛物线的顶点坐标，然后求出所求抛物线的顶点坐标，最后就可以求出原抛物线的解析式．
9.【答案】C
【解析】解：由抛物线与y轴的交点位置得到：c>1，选项①错误；
∵抛物线的对称轴为x=−b2a=1，∴2a+b=0，选项②正确；
由抛物线与x轴有两个交点，得到b2−4ac>0，即b2>4ac，选项③错误；
令抛物线解析式中y=0，得到ax2+bx+c=0，
∵方程的两根为x1，x2，且−b2a=1，及−ba=2，
∴x1+x2=−ba=2，选项④正确，
综上，正确的结论有②④．
故选C
由抛物线与y轴的交点在1的上方，得到c大于1，故选项①错误；由抛物线的对称轴为x=1，利用对称轴公式得到关于a与b的关系，整理得到2a+b=0，选项②正确；由抛物线与x轴的交点有两个，得到根的判别式大于0，整理可判断出选项③错误；令抛物线解析式中y=0，得到关于x的一元二次方程，利用根与系数的关系表示出两根之和，将得到的a与b的关系式代入可得出两根之和为2，选项④正确，即可得到正确的选项．
此题考查了二次函数图象与系数的关系，二次函数y=ax2+bx+c(a≠0)，a的符号由开口方向决定，c的符号由抛物线与y轴交点的位置确定，b的符号由a及对称轴的位置确定，抛物线与x轴交点的个数决定根的判别式的符号．
10.【答案】A
【解析】【分析】
由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况、二次函数图象上点的坐标特征以及二次函数的最值、二次函数的性质，对所得结论进行判断．
本题考查了二次函数图象与系数的关系和二次函数的性质等知识，掌握相关知识是关键．
【解答】
解：①由图象可知：a>0，c<0，
∵−b2a=1，
∴b=−2a<0，
∴abc>0，故①错误；
②∵抛物线与x轴有两个交点，
∴b2−4ac>0，
∴b2>4ac，故②正确；
③∵对称轴为直线x=1，
∴x=2与x=0时，y的值相同，
当x=2时，y=4a+2b+c<0，故③错误；
④当x=−1时，y=a−b+c>0，
∵b=−2a，
∴3a+c=a−b+c>0，故④正确；
⑤当x=1时，y的值最小，此时，y=a+b+c，
而当x=m时，y=am2+bm+c，
所以a+b+c≤am2+bm+c，
故a+b≤am2+bm，即a+b≤m(am+b)，故⑤正确，
⑥当x<−1时，y随x的增大而减小，故⑥错误，
综上，结论正确的有②④⑤，共3个．
故选：A．
11.【答案】112°
【解析】解：∵四边形ABCD内接于⊙O，∠ABC=68°，
∴∠ADC=180°−∠ABC=180°−68°=112°，
故答案为：112°．
根据圆内接四边形的性质即可得到结论．
本题考查了圆内接四边形的性质，熟练掌握圆内接四边形的性质是解题的关键．
12.【答案】x3=y−2x−92=y
【解析】解：设有x人，y辆车，根据题意可得：
x3=y−2x−92=y，
故答案为：x3=y−2x−92=y．
根据“每辆车乘坐3人，则空余两辆车；若每辆车乘坐2人，则有9人步行”，即可得出关于x，y的二元一次方程组，此题得解．
本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．
13.【答案】 10−1
【解析】【分析】
本题考查了翻折变换、矩形的性质以及勾股定理，利用作圆，找出A′C取最小值时点A′的位置是解题的关键．以点E为圆心，AE长度为半径作圆，连接CE，当点A′在线段CE上时，A′C的长取最小值，根据折叠的性质可知A′E=1，在Rt△BCE中利用勾股定理可求出CE的长度，用CE−A′E即可求出结论．
【解答】
解：以点E为圆心，AE长度为半径作圆，连接CE，当点A′在线段CE上时，A′C的长取最小值，如图所示．
根据折叠可知：A′E=AE=12AB=1，
在Rt△BCE中，BE=12AB=1，BC=3，∠B=90°，
∴CE= BE2+BC2= 10，
∴A′C的最小值=CE−A′E= 10−1．
故答案为： 10−1．
14.【答案】−8
【解析】解：作BC⊥x轴于C，AD⊥x轴于D，如图，则S△AOD=12×2=1，
在Rt△AOB中，tan∠BAO=OBOA=2，
∵∠AOD+∠BOC=90°，∠AOD+∠OAD=90°，
∴∠BOC=∠OAD，
∴Rt△AOD∽Rt△OBC，
∴S△OBCS△AOD=(OBOA)2=4，
∴S△OBC=4S△AOD=4，
∴12⋅|k|=4，
而k<0，
∴k=−8．
故答案为：−8．
作BC⊥x轴于C，AD⊥x轴于D，如图，利用反比例函数系数的几何意义得到S△AOD=1，再根据正切的意义得到tan∠BAO=OBOA=2，接着证明Rt△AOD∽Rt△OBC，利用相似三角形的性质得S△OBC=2S△AOD=4，所以12⋅|k|=4，然后根据反比例函数的性质确定k的值．
本题考查了反比例函数图象上点的坐标特征：反比例函数y=kx(k为常数，k≠0)的图象是双曲线，图象上的点(x,y)的横纵坐标的积是定值k，即xy=k.也考查了相似三角形的判定与性质．
15.【答案】π6
【解析】解：∵四边形OABC是平行四边形，OA=OC，
∴四边形OABC是菱形，
∴∠AOB=∠BOC，
∵OC/​/AB，
∴∠ABO=∠BOC，
∴∠ABO=∠AOB，
∴AB=OA=OB，
∴∠AOB=60°，
∵AB/​/OC，
∴S△ONC=S△OBC，
∴S阴影=S扇形OAB=60π×12360=π6．
故答案为π6．
根据题意证得AB=OA=OB，即可得到∠AOB=60°，根据同底等高的三角形面积相等得出S△ONC=S△OBC，即可得出S阴影=S扇形OAB．
本题主要考查的是扇形面积的计算，等边三角形的判断和性质，平行四边形的性质，以及圆周角定理．
16.【答案】20231012
【解析】解：由图形知a1=1×2，a2=2×3，a3=3×4，
∴an=n(n+1)，
∴原式=21×2+22×3+23×4+…+22022×2023+22023×2024
=2×(1−12+12−13+13−14+…+12023−12024)
=2×(1−12024)
=2×20232024
=20231012，
故答案为：20231012．
先根据已知图形得出an=n(n+1)，代入再利用1n(n+1)=1n−1n+1裂项化简可得答案．
本题主要考查图形的变化规律，解题的关键是根据已知图形得出an=n(n+1)及 1n(n+1)=1n−1n+1．
17.【答案】解：原式=(x−1)(x+1)−x(x−2)x(x+1)⋅(x+2)(x+1)2x−1
=x2−1−x2+2xx(x+1)⋅(x+2)(x+1)2x−1
=x+2x，
当x= 3时，
原式= 3+2 3=( 3+2)× 3 3× 3=3+2 33．
【解析】先计算括号内分式的减法、将除法转化为乘法，再计算乘法即可化简原式，继而将x的值代入计算即可．
本题主要考查分式的化简求值，解题的关键是掌握分式的混合运算顺序和运算法则．
18.【答案】解：(1)80÷40%=200(名)，
故答案为：200；
(2)200−80−60−20=40(名)，360°×40200=72°，补全条形统计图如图所示：
(3)用列表法表示所有可能出现的结果情况如下：
共有12种可能出现的结果，其中“1人认为效果很好，1人认为效果较好”的情况有甲丙，乙丙，丙甲，丙乙，有4种，
∴P(1人认为效果很好,1人认为效果较好)=412=13．
【解析】(1)从统计图可知，“A效果很好”的有80人，占调查人数的40%，可求出调查人数；
(2)求出“C效果一般”的人数即所占的百分比，即可求出相应的圆心角的度数，补全条形统计图；
(3)用列表法列举出所有可能出现的结果，从中找出“1人认为效果很好，1人认为效果较好”的结果数，进而求出概率．
本题考查条形统计图、扇形统计图的意义和制作方法，列表法或树状图求随机事件的概率，理解统计图中的数量关系，列出所有可能出现的结果情况是解决问题的关键．
19.【答案】
解：(1)如图，过M作MN⊥AB于N，交BA的延长线于N，
Rt△OMN中，∠NOM=60°，OM=1.2，
∴∠M=30°，
∴ON=12OM=0.6，
∴NB=ON+OB=3.3+0.6=3.9；
即点M到地面的距离是3.9米；
(2)取CE=0.65，EH=2.55，
∴HB=3.9−2.55−0.65=0.7，
过H作GH⊥BC，交OM于G，过O作OP⊥GH于P，
∵∠GOP=30°，
∴tan30°=GPOP= 33，
∴GP= 33OP=1.73×0.73≈0.404，
∴GH=3.3+0.404=3.704≈3.70>3.5，
∴货车能安全通过．
【解析】(1)构建直角△OMN，求ON的长，相加可得BN的长，即点M到地面的距离；
(2)左边根据要求留0.65米的安全距离，即取CE=0.65，车宽EH=2.55，计算高GH的长即可，与3.5作比较，可得结论．
本题考查解直角三角形的应用、锐角三角函数等知识，解题的关键是学会添加常用辅助线，在直角三角形解决问题，属于中考常考题型．
20.【答案】解：(1)设第二批每个挂件的进价为x元，则第一批每个挂件的进价为1.1x元，
根据题意可得，66001.1x+50=8000x，
解得x=40．
经检验，x=40是原分式方程的解，且符合实际意义，
∴第二批每个挂件的进价为40元．
(2)设每个售价定为y元，每周所获利润为w元，
根据题意可知，w=(y−40)[40+10(60−y)]=−10(y−52)2+1440，
∵−10<0，
∴当x≥52时，y随x的增大而减小，
∵40+10(60−y)≤90，
∴y≥55，
∴当y=55时，w取最大，此时w=−10(55−52)2+1440=1350．
∴当每个挂件售价定为55元时，每周可获得最大利润，最大利润是1350元．
【解析】(1)设第二批每个挂件的进价为x元，则第一批每个挂件的进价为1.1x元，根据题意列出方程，求解即可；
(2)设每个售价定为y元，每周所获利润为w元，则可列出w关于y的函数关系式，再根据“每周最多能卖90个”得出y的取值范围，根据二次函数的性质可得出结论．
本题综合考查分式方程和二次函数的应用，根据题意列出函数关系式是解题关键．
21.【答案】解：(1)∵B(3,1)，C(3,3)，
∴BC/​/y轴，BC=3−1=2，
又∵四边形ABCD是平行四边形，A(1,0)，
∴D(1,2)，
又∵点D(1,2)在反比例函数y=kx的图象上，
∴k=1×2=2，
∴反比例函数的关系式为y=2x；
(2)如图，过C作x轴、y轴的平行线，交双曲线于点P1、P2，
∵C(3,3)，
∴当x=3时，y=23，当y=3时，x=23，
∴P1(3,23)，P2(23,3)，
当点P在P1、P2之间的双曲线上时，直线PC，即直线y=ax+b(a≠0)，y随x的增大而增大，
∴点P的横坐标x的取值范围为23【解析】(1)根据点B、C的坐标特点，可得出BC//y轴，BC=2，再根据四边形ABCD是平行四边形，A(1,0)，可求出点D坐标，可求出反比例函数的关系式；
(2)过点C作x轴、y轴的平行线，交双曲线于点P1、P2，求出点P1、P2的坐标，即可求出答案．
本题考查反比例函数的图象和性质，一次函数的图象和性质，待定系数法求反比例函数的关系式，利用平行四边形的性质，得出点D的坐标是解决问题的关键．
22.【答案】(1)证明：如图1，由旋转得：∠EDF=90°，ED=DF，
∵四边形ABCD是正方形，
∴∠ADC=90°，AD=CD，
∴∠ADC=∠EDF，
即∠ADE+∠EDC=∠EDC+∠CDF，
∴∠ADE=∠CDF，
在△ADE和△CDF中，
∵AD=CD∠ADE=∠CDFDE=DF，
∴△ADE≌△CDF，
∴AE=CF；
(2)如图2，过F作OC的垂线，交BC的延长线于P，
∵O是BC的中点，且AB=BC=2 5，
∴OB= 5，
∵A，E，O三点共线，
由勾股定理得：AO=5，
∵OE=2，
∴AE=5−2=3，
由(1)知：△ADE≌△CDF，
∴∠DAE=∠DCF，CF=AE=3，
∵∠BAD=∠DCP，
∴∠OAB=∠PCF，
∵∠ABO=∠P=90°，
∴△ABO∽△CPF，
∴ABOB=CPPF=2 5 5=2，
∴CP=2PF，
设PF=x，则CP=2x，
在Rt△CPF中，由勾股定理得：32=x2+(2x)2，
解得：x1=3 55或x2=−3 55(舍)，
∴FP=3 55，CP=6 55，OP= 5+6 55=11 55，
在Rt△OPF中，由勾股定理得：OF= (3 55)2+(11 55)2= 26；
(3)如图3，由于OE=2，所以E点可以看作是在以O为圆心，2为半径的半圆上运动，
延长BA到G点，使得AG=OC，连接GE，
∵AE=CF，∠GAE=∠OCF，
∴△GAE≌△OCF，
∴GE=OF，
∴当OF最小时，即GE最小，此时O、E、G三点共线，
OG= OB2+GB2= ( 5)2+(3 5)2=5 2，
∴OF=GE=OG−OE=5 2−2，
∴OF的最小值是5 2−2．
【解析】本题是四边形的综合题，考查了正方形的性质、全等三角形的判定与性质及相似三角形的性质和判定、勾股定理，第三问判断最值是难点，将OF的长利用三角形全等转化为GE的长，从而解决问题．
(1)根据旋转的性质及正方形的性质，可证明△ADE≌△CDF，即可得到AE=CF；
(2)过F作OC的垂线，交BC的延长线于P，先利用：△ADE≌△CDF，求得CF的长，再利用△ABO∽△CPF，求得CP、PF的长，即可求得OF的长；
(3)延长BA到G点，使得AG=OC，连接GE，当O、E、G三点共线时，GE最小，即OF最小，根据勾股定理可得OG的长，从而得GE的长，即OF的最小值．
23.【答案】解：(1)设抛物线的解析式为y=a(x+1)(x−4)．
∵将C(0,−2)代入得：4a=2，解得a=12，
∴抛物线的解析式为y=12(x+1)(x−4)，即y=12x2−32x−2．
(2)过点D作DG⊥x轴于点G，交BC于点F，过点A作AK⊥x轴交BC的延长线于点K，
∴AK/​/DG，
∴△AKE∽△DFE，
∴DFAK=DEAE，
∴S1S2=S△BDES△ABE=DEAE=DFAK，
设直线BC的解析式为y=kx+b，
∴4k+b=0b=−2，解得k=12b=−2，
∴直线BC的解析式为y=12x−2，
∵A(−1,0)，
∴y=−12−2=−52，
∴AK=52，
设D(m,12m2−32m−2)，则F(m,12m−2)，
∴DF=12m−2−12m2+32m+2=−12m2+2m．
∴S1S2=−12m2+2m52=−15m2+45m=−15(m−2)2+45．
∴当m=2时，S1S2有最大值，最大值是45．
(3)符合条件的点P的坐标为(689,349)或(6+2 415,3+ 415).
∵l/​/BC，
∴直线l的解析式为y=12x，
设P(a1,a12)，
①当点P在直线BQ右侧时，如图2，过点P作PN⊥x轴于点N，过点Q作QM⊥直线PN于点M，
∵A(−1,0)，C(0,−2)，B(4,0)，
∴AC= 5，AB=5，BC=2 5，
∵AC2+BC2=AB2，
∴∠ACB=90°，
∵△PQB∽△CAB，
∴PQPB=ACBC=12，
∵∠QMP=∠BNP=90°，
∴∠MQP+∠MPQ=90°，∠MPQ+∠BPN=90°，
∴∠MQP=∠BPN，
∴△QPM∽△PBN，
∴QMPN=PMBN=PQPB=12，
∴QM=a14，PM=12(a1−4)=12a1−2，
∴MN=a1−2，ON−QM=a1−4−a14=34a1−4，
∴Q(34a1,a1−2)，
将点Q的坐标代入抛物线的解析式得12×(34a1)2−32×34a1−2=a1−2，
解得a1=0(舍去)或a1=689．
∴P(689,349).
②当点P在直线BQ左侧时，
由①的方法同理可得点Q的坐标为(54a1,2)．
此时点P的坐标为(6+2 415,3+ 415).
【解析】本题是二次函数综合题，考查了待定系数法求一次函数和二次函数的解析式，相似三角形的性质和判定，勾股定理的应用，二次函数的性质，三角形的面积等知识，熟练掌握相似三角形的判定与性质是解题的关键．
(1)设抛物线的解析式为为y=a(x−1)(x−4)，将点C的坐标代可求得a的值，从而得到抛物线的解析式；
(2)过点D作DG⊥x轴于点G，交BC于点F，过点A作AK⊥x轴交BC的延长线于点K，证明△AKE∽△DFE，得出DFAK=DEAE，则S1S2=S△BDES△ABE=DEAE=DFAK，求出直线BC的解析式为y=12x−2，设D(m,12m2−32m−2)，则F(m,12m−2)，可得出S1S2的关系式，由二次函数的性质可得出结论；
(3)设P(a1,a12)，①当点P在直线BQ右侧时，如图2，过点P作PN⊥x轴于点N，过点Q作QM⊥直线PN于点M，得出Q(34a1,a1−2)，将点Q的坐标代入抛物线的解析式求得a1的值即可，②当点P在直线BQ左侧时，由①的方法同理可得点Q的坐标为(54a1,2)，代入抛物线的解析可得出答案．
24.【答案】解：(1)AB+AC=AD；
(2)AB+AC= 2AD.理由如下：
如图②，延长AB至点M，使BM=AC，连接DM，
∵四边形ABDC内接于⊙O，
∴∠MBD=∠ACD，
∵∠BAD=∠CAD=45°，
∴BD=CD，
∴△MBD≌△ACD(SAS)，
∴MD=AD，∠M=∠CAD=45°，
∴MD⊥AD．
∴AM= 2AD，即AB+BM= 2AD，
∴AB+AC= 2AD；
(3)如图③，延长AB至点N，使BN=AC，连接DN，
∵四边形ABDC内接于⊙O，
∴∠NBD=∠ACD，
∵∠BAD=∠CAD，
∴BD=CD，
∴△NBD≌△ACD(SAS)，
∴ND=AD，∠N=∠CAD，
∴∠N=∠NAD=∠DBC=∠DCB，
∴△NAD∽△CBD，
∴ANBC=ADBD，
∴ADAN=BDBC，
又AN=AB+BN=AB+AC，BC=5，BD=4，
∴ADAB+AC=BDBC=45．
【解析】解：(1)如图①在AD上截取AE=AB，连接BE，
∵∠BAC=120°，∠BAC的平分线交⊙O于点D，
∴∠DBC=∠DAC=60°，∠DCB=∠BAD=60°，
∴△ABE和△BCD都是等边三角形，
∴∠DBE=∠ABC，AB=BE，BC=BD，
∴△BED≌△BAC(SAS)，
∴DE=AC，
∴AD=AE+DE=AB+AC；
故答案为：AB+AC=AD．
(2)AB+AC= 2AD.理由如下：
如图②，延长AB至点M，使BM=AC，连接DM，
∵四边形ABDC内接于⊙O，
∴∠MBD=∠ACD，
∵∠BAD=∠CAD=45°，
∴BD=CD，
∴△MBD≌△ACD(SAS)，
∴MD=AD，∠M=∠CAD=45°，
∴MD⊥AD．
∴AM= 2AD，即AB+BM= 2AD，
∴AB+AC= 2AD；
(3)如图③，延长AB至点N，使BN=AC，连接DN，
∵四边形ABDC内接于⊙O，
∴∠NBD=∠ACD，
∵∠BAD=∠CAD，
∴BD=CD，
∴△NBD≌△ACD(SAS)，
∴ND=AD，∠N=∠CAD，
∴∠N=∠NAD=∠DBC=∠DCB，
∴△NAD∽△CBD，
∴ANBC=ADBD，
∴ADAN=BDBC，
又AN=AB+BN=AB+AC，BC=5，BD=4，
∴ADAB+AC=BDBC=45．
(1)在AD上截取AE=AB，连接BE，由条件可知△ABE和△BCD都是等边三角形，可证明△BED≌△BAC，可得DE=AC，则AB+AC=AD；
(2)延长AB至点M，使BM=AC，连接DM，证明△MBD≌△ACD，可得MD=AD，证得AB+AC= 2AD；
(3)延长AB至点N，使BN=AC，连接DN，证明△NBD≌△ACD，可得ND=AD，∠N=∠CAD，证△NAD∽△CBD，可得ANBC=ADBD，可由AN=AB+AC，求出ADAB+AC的值．
本题属于圆的综合题，考查了圆周角定理，全等三角形的判定与性质，相似三角形的判定和性质，等边三角形的判定与性质等知识，解题的关键是正确作出辅助线解决问题．