






高中数学人教A版 (2019)选择性必修 第一册3.2 双曲线图片课件ppt
展开知识点一 双曲线的定义(一)教材梳理填空(1)定义:平面内与两个定点F1,F2的距离的 等于非零常数(小于______)的点的轨迹叫做双曲线.(2)焦点:两个定点 .(3)焦距: 的距离,表示为|F1F2|.(4)双曲线就是下列点的集合:P={M|||MF1|-|MF2||=2a,0<2a<|F1F2|}.
[微提醒] 平面内到两定点F1,F2的距离的差的绝对值为非零常数,即||MF1|-|MF2||=2a,关键词“平面内”.当2a<|F1F2|时,轨迹是双曲线;当2a=|F1F2|时,轨迹是分别以F1,F2为端点的两条射线;当2a>|F1F2|时,轨迹不存在.
(二)基本知能小试1.若动点P到点M(1,0),N(-1,0)的距离之差的绝对值为2,则点P的轨迹是( )A.双曲线 B.双曲线的一支C.两条射线 D.一条射线答案:C
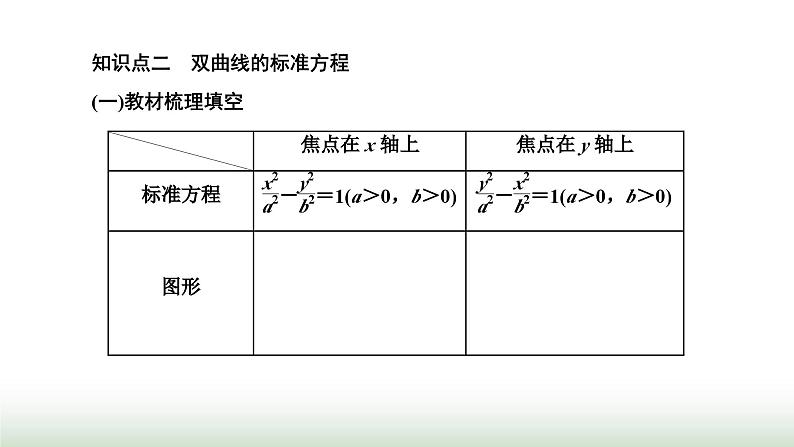
知识点二 双曲线的标准方程(一)教材梳理填空
[微提醒] 标准方程的代数特征:方程右边是1,左边是关于x,y的平方差,并且分母大小关系不确定.
解析:b2=c2-a2=72-52=24,故选C.答案:C
[解] (1)设|MF1|=16,根据双曲线的定义知||MF2|-16|=6,即|MF2|-16=±6,解得|MF2|=10或|MF2|=22.
(1)求双曲线上一点到某一焦点的距离时,若已知该点的横、纵坐标,则根据两点间距离公式可求结果;若已知该点到另一焦点的距离,则根据||PF1|-|PF2||=2a求解,注意对所求结果进行必要的验证(负数应该舍去,且所求距离应该不小于c-a).(2)在解决双曲线中与焦点三角形有关的问题时,首先要注意定义中的条件||PF1|-|PF2||=2a的应用;其次要利用余弦定理、勾股定理或三角形面积公式等知识进行运算,在运算中要注意整体思想和一些变形技巧的应用.
[对点练清]1.[多选]已知定点F1(-2,0),F2(2,0),在平面内满足下列条件的动点P的轨迹中为双曲线的是( )A.|PF1|-|PF2|=±2B.|PF1|-|PF2|=±3C.|PF1|-|PF2|=±4D.|PF1|2-|PF2|2=±4解析:|F1F2|=4,根据双曲线的定义知选A、B.答案:AB
题型三 双曲线标准方程的求法[学透用活]对双曲线标准方程的两点说明(1)只有当双曲线的两焦点F1,F2在坐标轴上,并且线段F1F2的垂直平分线也是坐标轴时得到的方程才是双曲线的标准方程.(2)标准方程中的两个参数a和b,确定了双曲线的形状和大小,是双曲线的定形条件,这里的b2=c2-a2与椭圆中的b2=a2-c2相区别,且椭圆中a>b>0,而双曲线中a,b大小不确定.
[方法技巧] 1.求双曲线标准方程的步骤
2.双曲线标准方程的两种求法
[提醒] 若焦点的位置不明确,应注意分类讨论,也可以设双曲线方程为mx2+ny2=1的形式,注意标明条件mn<0.
[对点练清]如图,已知双曲线以长方形ABCD的顶点A,B为左、右焦点,且过C,D两顶点.若AB=4,BC=3,求此双曲线的标准方程.
求与双曲线有关的点的轨迹问题的方法(1)列出等量关系,化简得到方程.(2)寻找几何关系,由双曲线的定义,得出对应的方程.[提醒] (1)分清双曲线的焦点所在的坐标轴是哪个.(2)检验所求的轨迹对应的是双曲线的一支还是两支.
2. 已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,求动圆圆心M的轨迹方程.解:如图所示,设动圆M与圆C1及圆C2分别外切于点A和B,根据两圆外切的条件,得|MC1|=|AC1|+|MA|,|MC2|=|BC2|+|MB|.∵|MA|=|MB|,∴|MC2|-|MC1|=|BC2|-|AC1|=3-1=2.
二、应用性——强调学以致用2.某工程需要开挖一个横截面为半圆的柱形隧道,挖出的土只能沿道路AP或BP运到P处(如图),已知|AP|=100,|BP|=150,∠APB=60°,试说明怎样运土才能最省工.[析题建模] 首先抽象为数学问题,半圆中的点可分为三类:(1)沿AP到点P较近;(2)沿BP到点P较近;(3)沿AP,BP到点P的路程相等.显然,第三类点是第一、二类的分界点.设点M是分界线上的任意一点,则有|MA|+|PA|=|MB|+|PB|.于是|MA|-|MB|=|PB|-|PA|=150-100=50.由此发现点M满足条件:点M到点A与到点B的距离的差等于常数50.由双曲线的定义知,点M在以A,B为左、右焦点的双曲线的右支上,问题转化为求此双曲线的方程.
高中人教A版 (2019)第三章 圆锥曲线的方程3.2 双曲线集体备课ppt课件: 这是一份高中人教A版 (2019)第三章 圆锥曲线的方程3.2 双曲线集体备课ppt课件,共38页。PPT课件主要包含了目录索引,本节要点归纳等内容,欢迎下载使用。
人教A版 (2019)3.2 双曲线作业ppt课件: 这是一份人教A版 (2019)3.2 双曲线作业ppt课件,共18页。
高中数学人教A版 (2019)选择性必修 第一册3.2 双曲线课文配套课件ppt: 这是一份高中数学人教A版 (2019)选择性必修 第一册3.2 双曲线课文配套课件ppt,共19页。PPT课件主要包含了复习引入,新知探究,符号表达,双曲线的一支,两条射线,轨迹不存在,定义辨析,双曲线标准方程的推导,两边平方整理得,焦点位置等内容,欢迎下载使用。













