初中数学北师大版七年级下册2 用关系式表示的变量间关系当堂达标检测题

这是一份初中数学北师大版七年级下册2 用关系式表示的变量间关系当堂达标检测题，共10页。试卷主要包含了以等腰三角形底角的度数x等内容，欢迎下载使用。
1．已知小明从A地到B地，速度为4千米/小时，A、B两地相距3千米，若用x（小时）表示行走的时间，y（千米）表示余下的路程，则y与x之间的函数表达式是（ ）
A．y＝4xB．y＝4x﹣3C．y＝﹣4xD．y＝﹣4x+3
2．佳佳花3000元买台空调，耗电0.7度/小时，电费1.5元/度．持续开x小时后，产生电费y（元）与时间（小时）之间的函数关系式是（ ）
A．y＝1.05xB．y＝0.7x
C．y＝1.5xD．y＝3000+1.5x
3．小王每天记忆10个英语单词，x天后他记忆的单词总量为y个，则y与x之间的函数关系式是（ ）
A．y＝10+xB．y＝10xC．y＝100xD．y＝10x+10
4．以等腰三角形底角的度数x（单位：度）为自变量，顶角的度数y为因变量的函数关系式为（ ）
A．y＝180﹣2x（0＜x＜90）B．y＝180﹣2x（0＜x≤90）
C．y＝180﹣2x（0≤x＜90）D．y＝180﹣2x（0≤x≤90）
5．一个正方形的边长为5cm，它的各边边长减少xcm后，得到的新正方形的周长为ycm，y与x的函数关系式为（ ）
A．y＝20﹣4xB．y＝4x﹣20C．y＝20﹣xD．以上都不对
6．已知矩形的周长为16cm，其中一边长为xcm，面积为ycm2，则这个矩形的面积y与边长x之间的关系可表示为（ ）
A．y＝x2B．y＝（8﹣x）2C．y＝x（8﹣x）D．y＝2（8﹣x）
7．甲乙两地间的路程为90km，汽车从甲地驶往乙地，它的平均速度为60km/h，则汽车距乙地的路程s（km）与行驶时间t（h）之间的函数解析式是（ ）
A．s＝60t（t≥0）B．s＝60t（）
C．s＝90﹣6t（t≥0）D．s＝90﹣60t（）
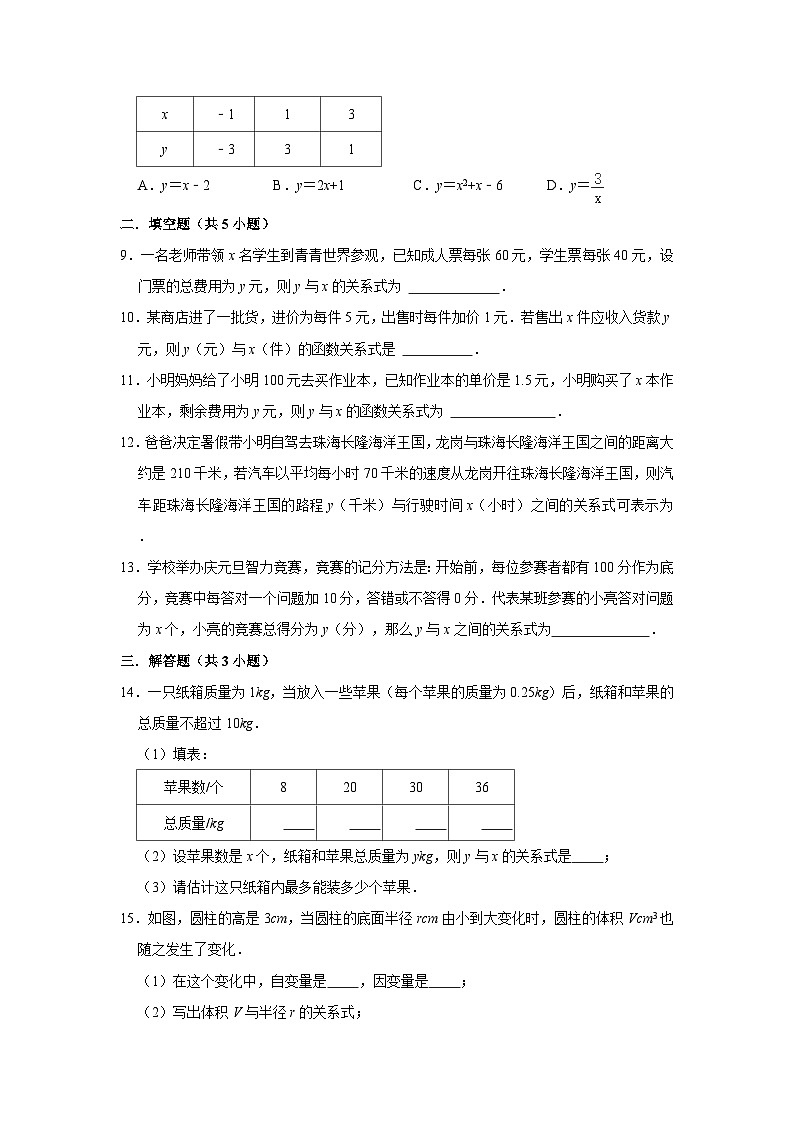
8．已知两个变量x和y，它们之间的3组对应值如表所示，则y与x之间的函数关系式可能是（ ）
A．y＝x﹣2B．y＝2x+1C．y＝x2+x﹣6D．y＝
二．填空题（共5小题）
9．一名老师带领x名学生到青青世界参观，已知成人票每张60元，学生票每张40元，设门票的总费用为y元，则y与x的关系式为 ．
10．某商店进了一批货，进价为每件5元，出售时每件加价1元．若售出x件应收入货款y元，则y（元）与x（件）的函数关系式是 ．
11．小明妈妈给了小明100元去买作业本，已知作业本的单价是1.5元，小明购买了x本作业本，剩余费用为y元，则y与x的函数关系式为 ．
12．爸爸决定暑假带小明自驾去珠海长隆海洋王国，龙岗与珠海长隆海洋王国之间的距离大约是210千米，若汽车以平均每小时70千米的速度从龙岗开往珠海长隆海洋王国，则汽车距珠海长隆海洋王国的路程y（千米）与行驶时间x（小时）之间的关系式可表示为 ．
13．学校举办庆元旦智力竞赛，竞赛的记分方法是：开始前，每位参赛者都有100分作为底分，竞赛中每答对一个问题加10分，答错或不答得0分．代表某班参赛的小亮答对问题为x个，小亮的竞赛总得分为y（分），那么y与x之间的关系式为 ．
三．解答题（共3小题）
14．一只纸箱质量为1kg，当放入一些苹果（每个苹果的质量为0.25kg）后，纸箱和苹果的总质量不超过10kg．
（1）填表：
（2）设苹果数是x个，纸箱和苹果总质量为ykg，则y与x的关系式是 ；
（3）请估计这只纸箱内最多能装多少个苹果．
15．如图，圆柱的高是3cm，当圆柱的底面半径rcm由小到大变化时，圆柱的体积Vcm3也随之发生了变化．
（1）在这个变化中，自变量是 ，因变量是 ；
（2）写出体积V与半径r的关系式；
（3）当底面半径由1cm到10cm变化时，通过计算说明圆柱的体积增加了多少cm3．
16．一个长方形的长是6，宽是x，周长是y，面积是s．
（1）写出y随x变化而变化的关系式；
（2）写出s随x变化而变化的关系式；
（3）当s＝60时，x等于多少？y等于多少？
用关系式表示的变量间关系
参考答案与试题解析
一．选择题（共8小题）
1．已知小明从A地到B地，速度为4千米/小时，A、B两地相距3千米，若用x（小时）表示行走的时间，y（千米）表示余下的路程，则y与x之间的函数表达式是（ ）
A．y＝4xB．y＝4x﹣3C．y＝﹣4xD．y＝﹣4x+3
【分析】直接利用总路程﹣行驶的路程＝余下的路程，进而得出答案．
【解答】解：用x（小时）表示行走的时间，y（千米）表示余下的路程，
则y与x之间的函数表达式是：y＝3﹣4x＝﹣4x+3．
故选：D．
【点评】此题主要考查了根据实际问题列一次函数解析式，正确理解题意表示出行驶路程是解题的关键．
2．佳佳花3000元买台空调，耗电0.7度/小时，电费1.5元/度．持续开x小时后，产生电费y（元）与时间（小时）之间的函数关系式是（ ）
A．y＝1.05xB．y＝0.7x
C．y＝1.5xD．y＝3000+1.5x
【分析】根据电费＝每度电费的价格×每小时耗电×时间解答即可．
【解答】解：根据题意，得y＝1.5×0.7×x，
即y＝1.05x．
故选：A．
【点评】本题考查了函数关系式，能够正确找出已知量和未知量之间的函数关系是解题的关键．
3．小王每天记忆10个英语单词，x天后他记忆的单词总量为y个，则y与x之间的函数关系式是（ ）
A．y＝10+xB．y＝10xC．y＝100xD．y＝10x+10
【分析】根据每天记忆10个英语单词，x天后他记忆的单词总量为y个，即可得出y与x之间的函数关系式．
【解答】解：根据题意，得y＝10x，
故选：B．
【点评】此题主要考查了一次函数关系式，能够根据题意正确求出函数关系式是解题关键．
4．以等腰三角形底角的度数x（单位：度）为自变量，顶角的度数y为因变量的函数关系式为（ ）
A．y＝180﹣2x（0＜x＜90）B．y＝180﹣2x（0＜x≤90）
C．y＝180﹣2x（0≤x＜90）D．y＝180﹣2x（0≤x≤90）
【分析】根据三角形内角和定理得2x+y＝180，然后变形就可以求出y与x的函数解析式．
【解答】解：y＝180﹣2x，
∵，
∵x为底角度数
∴0＜x＜90．
故选：A．
【点评】本题考查了函数关系式，解决本题的关键是利用三角形内角和定理求一次函数的解析式．
5．一个正方形的边长为5cm，它的各边边长减少xcm后，得到的新正方形的周长为ycm，y与x的函数关系式为（ ）
A．y＝20﹣4xB．y＝4x﹣20C．y＝20﹣xD．以上都不对
【分析】一个正方形的边长为5cm，它的边长减少xcm后得到的新正方形的边长为5﹣x，即可得到周长为y＝4（5﹣x）．
【解答】解：由题意得：原正方形边长为5，减少xcm后边长为5﹣x，
则周长y与边长x的函数关系式为：y＝20﹣4x．
故选：A．
【点评】此题主要考查了由实际问题列函数关系式，函数解析式中，通常等式的右边的式子中的变量是自变量，等式左边的那个字母表示自变量的函数．
6．已知矩形的周长为16cm，其中一边长为xcm，面积为ycm2，则这个矩形的面积y与边长x之间的关系可表示为（ ）
A．y＝x2B．y＝（8﹣x）2C．y＝x（8﹣x）D．y＝2（8﹣x）
【分析】直接利用长方形面积求法得出答案．
【解答】解：∵长方形的周长为16cm，其中一边长为xcm，
∴另一边长为：（8﹣x）cm，
∴矩形的面积y与边长x之间的关系可表示为y＝（8﹣x）x．
故选：C．
【点评】此题主要考查了函数关系式，正确表示出长方形的另一边长是解题关键．
7．甲乙两地间的路程为90km，汽车从甲地驶往乙地，它的平均速度为60km/h，则汽车距乙地的路程s（km）与行驶时间t（h）之间的函数解析式是（ ）
A．s＝60t（t≥0）B．s＝60t（）
C．s＝90﹣6t（t≥0）D．s＝90﹣60t（）
【分析】根据速度乘以时间，可得行驶路程，根据两地距离减去行驶路程，可得汽车距乙地的路程．
【解答】解：由题意可得，汽车距乙地的路程s（km）与行驶时间t（h）之间的关系式是s＝90﹣60t（），
故选：D．
【点评】此题主要考查了根据实际问题列函数关系式，关键是正确理解题意，找出题目中的等量关系．
8．已知两个变量x和y，它们之间的3组对应值如表所示，则y与x之间的函数关系式可能是（ ）
A．y＝x﹣2B．y＝2x+1C．y＝x2+x﹣6D．y＝
【分析】观察这几组数据，找到其中的规律，然后再答案中找出符合要求的关系式．
【解答】解：A．将表格对应数据代入，不符合方程y＝x﹣2，故A选项错误；
B．将表格对应数据代入，不符合方程y＝2x+1，故B选项错误；
C．将表格对应数据代入，不符合方程y＝x2+x﹣6，故C选项错误；
D．将表格对应数据代入，符合方程，故D选项正确．
故选：D．
【点评】此题主要考查了求函数关系式，本题是开放性题目，需要找出题目中的两未知数的对应变化规律是解题关键．
二．填空题（共5小题）
9．一名老师带领x名学生到青青世界参观，已知成人票每张60元，学生票每张40元，设门票的总费用为y元，则y与x的关系式为 y＝40x+60 ．
【分析】根据学生人数乘以学生票价，可得学生的总票价，根据师生的总票价，可得函数关系式．
【解答】解：由题意，得
y＝40x+60，
故答案为：y＝40x+60．
【点评】本题考查了函数关系式．解题的关键是明确学生的票价加老师的票价等于总票价．
10．某商店进了一批货，进价为每件5元，出售时每件加价1元．若售出x件应收入货款y元，则y（元）与x（件）的函数关系式是 y＝6x． ．
【分析】单价为（5+1）元，根据总价＝单价×数量列出关系式即可．
【解答】解：依题意有：y＝（5+1）x＝6x．
故y与x的函数关系式是：y＝6x．
故答案为：y＝6x．
【点评】本题主要考查了列函数关系式．根据题意，找到所求量的等量关系是解题的关键．
11．小明妈妈给了小明100元去买作业本，已知作业本的单价是1.5元，小明购买了x本作业本，剩余费用为y元，则y与x的函数关系式为 y＝100﹣1.5x ．
【分析】根据剩余费用＝总金额﹣单价×数量解答即可．
【解答】解：由题意，得
y＝100﹣1.5x．
故答案为：y＝100﹣1.5x．
【点评】本题考查了函数关系式．能够正确利用剩余费用＝总金额﹣单价×数量列出关系式是解题的关键．
12．爸爸决定暑假带小明自驾去珠海长隆海洋王国，龙岗与珠海长隆海洋王国之间的距离大约是210千米，若汽车以平均每小时70千米的速度从龙岗开往珠海长隆海洋王国，则汽车距珠海长隆海洋王国的路程y（千米）与行驶时间x（小时）之间的关系式可表示为 y＝210﹣70x ．
【分析】汽车距珠海长隆海洋王国的路程＝总路程﹣走过的路程，根据题意写出函数关系式即可．
【解答】解：根据题意得：y＝210﹣70x．
故答案为：y＝210﹣70x．
【点评】本题考查一次函数的关系式，解题的关键是根据题意明白各个量之间的关系．
13．学校举办庆元旦智力竞赛，竞赛的记分方法是：开始前，每位参赛者都有100分作为底分，竞赛中每答对一个问题加10分，答错或不答得0分．代表某班参赛的小亮答对问题为x个，小亮的竞赛总得分为y（分），那么y与x之间的关系式为 y＝10x+100 ．
【分析】根据题意列出关系式即可．
【解答】解：根据题意得：
y＝10x+100．
故答案为：y＝10x+100．
【点评】此题考查了一次函数，解题的关键是根据题意得出关系式进行解答．
三．解答题（共3小题）
14．一只纸箱质量为1kg，当放入一些苹果（每个苹果的质量为0.25kg）后，纸箱和苹果的总质量不超过10kg．
（1）填表：
（2）设苹果数是x个，纸箱和苹果总质量为ykg，则y与x的关系式是 y＝1+0.25x ；
（3）请估计这只纸箱内最多能装多少个苹果．
【分析】（1）根据纸箱的质量+每个苹果的质量×个数＝总质量计算即可；
（2）根据纸箱和苹果总质量＝纸箱的质量+每个苹果的质量×个数列关系式即可；
（3）根据纸箱和苹果得的总质量不超过10kg列不等式解答即可．
【解答】解：（1）1+0.25×8＝3（kg），
1+0.25×20＝6（kg），
1+0.25×30＝8.5（kg），
1+0.25×36＝10（kg），
填表如下：
故答案为：3，6，8.5，10；
（2）根据题意，得y＝1+0.25x；
故答案为：y＝1+0.25x；
（3）设这只纸箱内装了x个苹果，根据题意得
0.25x+1≤10
解得x≤36
所以的最大值是36．
答：估计这只纸箱内最多能装36个苹果．
【点评】本题主要考查函数关系式和不等式的应用．解题的关键是掌握不等式的应用，能够找出题中的等量关系列出不等式．
15．如图，圆柱的高是3cm，当圆柱的底面半径rcm由小到大变化时，圆柱的体积Vcm3也随之发生了变化．
（1）在这个变化中，自变量是 r ，因变量是 V ；
（2）写出体积V与半径r的关系式；
（3）当底面半径由1cm到10cm变化时，通过计算说明圆柱的体积增加了多少cm3．
【分析】（1）根据函数间两变量的变化关系，可得答案；
（2）根据圆柱的体积公式，可得函数解析式；
（3）利用圆柱的体积计算方法计算增加的体积即可．
【解答】解：（1）在这个变化过程中，自变量是r，因变量是V．
故答案为：r，V；
（2）圆柱的体积V与底面半径r的关系式是 V＝3πr2．
（3）（π×102﹣π×12）×3＝297π（cm3）．
所以当底面半径由1cm到10cm变化时，圆柱的体积增加了297πcm3．
【点评】本题考查了函数关系式，利用圆柱的体积公式得出函数关系式是解题的关键．
16．一个长方形的长是6，宽是x，周长是y，面积是s．
（1）写出y随x变化而变化的关系式；
（2）写出s随x变化而变化的关系式；
（3）当s＝60时，x等于多少？y等于多少？
【分析】（1）根据长方形的周长公式，可得y和x之间的函数解析式；
（2）根据长方形的面积公式，可得s与x之间函数解析式；
（3）把s＝60代入函数关系式即可得到x，y的值．
【解答】解：（1）y和x之间的函数关系式为y＝2（6+x）＝2x+12（x＞0）；
（2）s与x之间函数关系式为s＝6x（x＞0）；
（3）当s＝60时，即60＝6x，
∴x＝10，
∴y＝2×10+12＝32．
【点评】本题考查了函数关系式．解题的关键是能够正确利用长方形的周长和面积公式，长方形的宽与周长，长方形的长与长方形的宽的关系．
x
﹣1
1
3
y
﹣3
3
1
苹果数/个
8
20
30
36
总质量/kg




x
﹣1
1
3
y
﹣3
3
1
苹果数/个
8
20
30
36
总质量/kg
3
6
8.5
10
苹果数/个
8
20
30
36
总质量/kg
3
6
8.5
10