适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式第3节二次函数及其性质课件新人教A版

这是一份适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式第3节二次函数及其性质课件新人教A版，共36页。PPT课件主要包含了强基础固本增分，研考点精准突破，目录索引，题组三连线高考，考点二二次函数的图象，ABD，-∞-2等内容，欢迎下载使用。

1.理解二次函数的图象与性质.2.能够利用二次函数的图象与性质解决相关问题.
1.二次函数解析式的三种形式(1)一般式:f(x)=ax2+bx+c(a≠0).(2)顶点式:若顶点为(m,n),则f(x)=　　　　　　　　　. (3)零点式:若两个零点为x1,x2,则f(x)=　　　　　　　　　. 
a(x-m)2+n(a≠0)
a(x-x1)(x-x2)(a≠0)
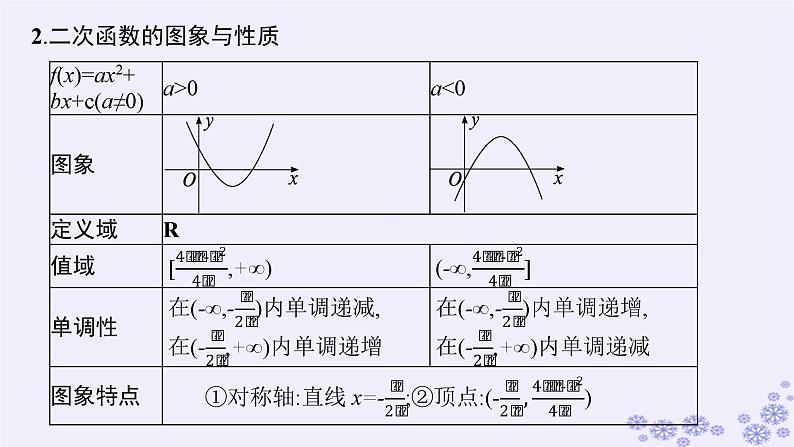
2.二次函数的图象与性质
微思考如何求解二次函数f(x)=ax2+bx+c(a>0)在闭区间[m,n]上的最值?
常用结论1.若f(x)=ax2+bx+c(a≠0),则当b=0时f(x)为偶函数,当b≠0时f(x)为非奇非偶函数.2.若f(x)=ax2+bx+c(a≠0)的顶点坐标为(m,n),则其图象的对称轴为直线x=m,其最值为n;若有f(m)=f(n),则其图象的对称轴为直线x= .
题组一思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)1.函数f(x)=sin2x+4sin x-1的最小值为-5.(　　)2.若二次函数f(x)=ax2+bx+c(a≠0)的图象不经过第一象限,则必有a<0.(　　)3.ax2+bx+c>0的充要条件是a>0且b2-4ac<0.(　　)4.若f(x)=a(x-m)2+n(a>0)且f(x1)>f(x2),则|x1-m|>|x2-m|.(　　)
题组二回源教材5.(人教B版必修第一册3.1.2节练习B第5题改编)函数f(x)=2x2+6x,x∈[-5,3]的单调递增区间是　　　　,单调递减区间是　　　　. 
6.(人教B版必修第一册140页复习题B组第4题)已知f(x)=x2+2(a-1)x+2在(-∞,4]上是减函数,求a的取值范围.
解 依题意有-(a-1)≥4,解得a≤-3.
8.(2022·北京,14)设函数f(x)= 若f(x)存在最小值,则a的一个取值为　　　　　;a的最大值为　　　　　. 
解析 根据题意可以用0,2作为a的取值的分界点,研究函数f(x)的性质.当a<0时,f(x)=-ax+1,x2时,f(x)=-ax+1,x考点一二次函数的解析式
例1(1)(2024·山东潍坊检测)已知二次函数图象的顶点坐标为(1,1),且过(2,2)点,则该二次函数的解析式为(　　)A.y=x2-1B.y=-(x-1)2+1C.y=(x-1)2+1D.y=(x-1)2-1
解析 由顶点坐标可设二次函数的解析式为y=a(x-1)2+1,将点(2,2)的坐标代入函数解析式得a+1=2,解得a=1,所以二次函数解析式为y=(x-1)2+1,故选C.
(2)已知二次函数f(x)的图象经过三点A(-1,6),B(1,0),C(2,-9),则f(x)的解析式为　　　　　　　　. 
f(x)=-2x2-3x+5
(3)(2024·山西太原模拟)已知二次函数f(x)的两个零点分别是1和5,图象开口向上,且f(x)在区间[-1,4]上的最大值为18,则函数f(x)的解析式为　　　 　　　　　. 
例2(多选题)(2024·浙江湖州检测)已知二次函数f(x)=ax2+bx+c(a≠0,a,b,c为常数)图象的对称轴为直线x=1,其图象如上图所示,则下列选项正确的有(　　)A.|abc|+abc=0B.4a+2b+c<0C.当x∈[a,1-a]时,f(x)≤c-a2
[对点训练1](多选题)(2024·江苏扬州检测)设abc<0,则函数y=ax2+bx+c的图象可能是(　 　)
考点三二次函数的性质及其应用(多考向探究预测)
考向1二次函数的单调性例3(2024·湖北随州模拟)已知函数f(x)=(m+1)x2-mx-1(m∈R)在区间(0,+∞)上单调递增,则实数m的取值范围为　　　　. 
解析 若m+1=0,则m=-1,此时f(x)=x-1,在区间(0,+∞)上单调递增,符合题意;
综上所述,实数m的取值范围为[-1,0].
变式探究1 (变条件)本例中,函数解析式不变,若函数在区间[1,2]上单调递减,则实数m的取值范围为　　　　. 
变式探究2(变条件)本例中,函数解析式不变,若函数在区间[-3,-2]上不单调,则实数m的取值范围为　　　　. 
变式探究3(变条件)本例中,若函数解析式不变,且对于任意的x1,x2∈(0,+∞),当x1≠x2时都有 >-2,求实数m的取值范围.
考向2二次函数的最值例4(2024·湖北武汉联考)已知函数y=ax2-2ax+1+b(a>0).(1)若a=b=1,求y在[t,t+1]上的最大值;(2)若函数在区间[2,4]上的最大值为9,最小值为1,求实数a,b的值.
(2)因为函数的图象开口向上,且对称轴方程为x=1∉[2,4],所以函数在区间[2,4]上单调递增,所以当x=2时,y取得最小值b+1;当x=4时,y取得最大值16a-8a+1+b=8a+1+b.
[对点训练2](2024·云南昆明模拟)已知二次函数f(x)=ax2+bx+c(a≠0)的图象过点(-2,0)和原点,且对于任意x∈R,都有f(x)≥2x.(1)求函数f(x)的表达式;(2)设g(x)=f(x)+2mx,求函数g(x)在区间[0,1]上的最小值.
(2)g(x)=f(x)+2mx=x2+(2+2m)x,则g(x)的对称轴为直线x=-m-1,当-m-1≤0,即m≥-1时,函数在区间[0,1]上单调递增,故g(x)在区间[0,1]上的最小值为g(0)=0;当-m-1≥1,即m≤-2时,函数在区间[0,1]上单调递减,故g(x)在区间[0,1]上的最小值为g(1)=3+2m;当0<-m-1<1,即-2考向3二次函数的综合应用例5(2024·北京海淀模拟)已知函数y=acs x+cs 2x,则“对任意的实数x,y≤3”是“a≤2”的(　　)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
f(t)max=f(-1)=1-a≤3,解得-2≤a<0.综上,“对任意的实数x,y≤3”等价于-2≤a≤2,所以“对任意的实数x,y≤3”是“a≤2”的充分不必要条件,故选A.