






适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式第4节一元二次方程不等式课件新人教A版
展开1.会结合二次函数的图象,判断一元二次方程根的存在性及根的个数.2.能借助二次函数求解一元二次不等式,能用集合表示一元二次不等式的解集.3.借助二次函数的图象,了解一元二次不等式与相应函数、方程的联系.
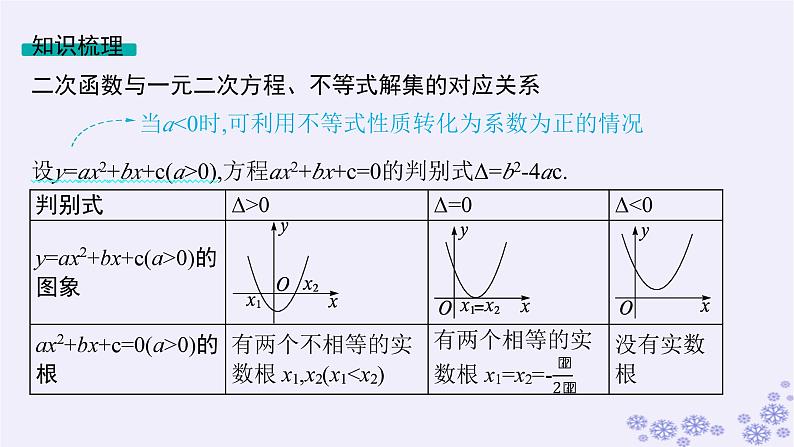
二次函数与一元二次方程、不等式解集的对应关系
设y=ax2+bx+c(a>0),方程ax2+bx+c=0的判别式Δ=b2-4ac.
当a<0时,可利用不等式性质转化为系数为正的情况
{x|x
{x|x1
题组一思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)1.若不等式ax2+bx+c<0的解集为(x1,x2),则a>0.( )2.不等式 ≥0与不等式(x-a)(x-b)≥0等价.( )3.若不等式ax2+bx+c<0中b2-4ac<0,则其解集为⌀.( )4.函数y=lg(x2+2x+2)的定义域为R.( )
题组二回源教材5.(人教A版必修第一册58页复习参考题2第6题)当k取什么值时,一元二次不等式2kx2+kx- <0对一切实数x都成立.
6.(人教B版必修第一册81页习题2-2B第7题)已知-x2+ax+b≥0的解集是[-2,3],求x2-5ax+b<0的解集.
解 -x2+ax+b≥0化为x2-ax-b≤0,其解集为[-2,3],所以方程x2-ax-b=0的两根是-2,3,因此a=1,b=6,不等式x2-5ax+b<0即为x2-5x+6<0,解集为(2,3).
题组三连线高考7.(2020·全国Ⅰ,理2)设集合A={x|x2-4≤0},B={x|2x+a≤0},且A∩B={x|-2≤x≤1},则a=( )A.-4B.-2C.2D.4
x∈[a,b]时,1≤f(x)≤3,则b-a的最大值是 .
考点一 一元二次不等式的解法(多考向探究预测)
考向1不含参数的一元二次不等式的解法例1(1)不等式(x-2)(x+3)>x-2的解集为 .
(-∞,-2)∪(2,+∞)
解析 不等式(x-2)(x+3)>x-2可化为(x-2)(x+2)>0,所以不等式的解集为(-∞,-2)∪(2,+∞).
(2)函数f(x)= 的定义域为 .
(3)不等式0≤2x2+x-3<7的解集为 .
考向2简单的分式不等式的解法例2(1)(2024·陕西渭南检测)不等式 ≥1的解集为 .
(2)(2024·河南郑州检测)函数f(x)= 的定义域为 .
(3)(2024·上海徐汇模拟)不等式 ≥1的解集为 .
解析 由于x2+2x+3>0恒成立,原不等式可化为x+5≥x2+2x+3,即x2+x-2≤0,解得-2≤x≤1,故解集为[-2,1].
考向3含参数的一元二次不等式的解法例3若a>0,解关于x的不等式ax2-2(a+1)x+4<0.
解 由于ax2-2(a+1)x+4<0⇒(ax-2)(x-2)<0.
变式探究1(变条件)本例中,若“a>0”改为“a∈R”,再解不等式.
解 ax2-2(a+1)x+4<0⇒(ax-2)(x-2)<0.当a=0时,不等式可化为-2(x-2)<0,解不等式得x>2;
变式探究2本例中,若条件不变,且关于x的不等式ax2-2(a+1)x+4<0的解集中,只有1个整数,求实数a的取值范围.
[对点训练1]解关于x的不等式x2-2mx+m+1>0.
解 不等式对应方程x2-2mx+m+1=0的判别式Δ=(-2m)2-4(m+1)=4(m2-m-1).
考点二“三个二次”之间的关系及其应用
A.-2B.1C.2D.8
[对点训练2](2024·江西南昌模拟)已知关于x的不等式mx2+nx+6m>0的解集为(2,3),则不等式mx
考向1在R上的恒成立问题例5(2024·云南红河检测)不等式ax2-ax+a+1>0对∀x∈R恒成立,则实数a的取值范围为( )A.(0,+∞)B.[0,+∞)
解析 ①当a=0时,不等式化为1>0,恒成立;②当a≠0时,只需
综上,a≥0,即实数a的取值范围为[0,+∞),故选B.
[对点训练3](多选题)(2024·湖南长沙模拟)“不等式mx2+mx-4≤2x2+2x-1对任意实数x均成立”的一个充分不必要条件是( )A.-10
解析 依题意,即不等式(m-2)x2+(m-2)x-3≤0恒成立.当m=2时,不等式可化为-3<0恒成立;当m<2时,由(m-2)2+12(m-2)≤0,解得-10≤m<2.综上,“不等式mx2+mx-4≤2x2+2x-1对任意实数x均成立”的充要条件是-10≤m≤2,因此一个充分不必要条件可以是A,B,C,故选ABC.
考向2在给定区间上的恒成立问题例6(2024·四川雅安模拟)对任意的x∈(1,4),不等式ax2-2x+2>0都成立,则实数a的取值范围是( )
[对点训练4](2024·江苏徐州模拟)已知“∃x∈[1,2],x2+tx+2t-3>0”为假命题,则实数t的取值范围是 .
解析 依题意,该命题的否定“∀x∈[1,2],x2+tx+2t-3≤0”为真命题.
考向3给定参数范围的恒成立问题例7(2024·浙江温州模拟)已知a∈[-1,1]时,不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为( )A.(-∞,2)∪(3,+∞)B.(-∞,1)∪(2,+∞)C.(-∞,1)∪(3,+∞)D.(1,3)
解析 a∈[-1,1]时,不等式x2+(a-4)x+4-2a>0恒成立,可转化为关于a的函数f(a)=(x-2)a+x2-4x+4>0对任意a∈[-1,1]恒成立,则满足 解得x<1或x>3,即x的取值范围为(-∞,1)∪(3,+∞).
[对点训练5](2024·重庆万州模拟)若命题“∃a∈[-1,3],ax2-(2a-1)x+3-a<0”为假命题,则实数x的取值范围为( )
适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式素能培优一一元二次方程根的分布课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式素能培优一一元二次方程根的分布课件新人教A版,共19页。PPT课件主要包含了-∞-3等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式课时规范练6一元二次方程不等式课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式课时规范练6一元二次方程不等式课件新人教A版,共18页。PPT课件主要包含了BCD等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式课时规范练4基本不等式课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式课时规范练4基本不等式课件新人教A版,共19页。PPT课件主要包含了BCD等内容,欢迎下载使用。












