第1-3单元阶段高频易错题检测卷（拔高训练）2023-2024学年六年级数学下册重点方法与技巧（人教版）

这是一份第1-3单元阶段高频易错题检测卷（拔高训练）2023-2024学年六年级数学下册重点方法与技巧（人教版），文件包含答案解析docx、第1-3单元阶段高频易错题检测卷拔高训练-练透核心考点2023-2024学年六年级数学下册重点方法与技巧A4版人教版docx、第1-3单元阶段高频易错题检测卷拔高训练-练透核心考点2023-2024学年六年级数学下册重点方法与技巧A3版人教版docx等3份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

1．B
【分析】根据正数＞0＞负数，负数大小比较就是看负号后面的数字，数字越大的反而越小，跟正数恰好相反，据此解答即可。
【详解】因为1＞﹣1＞﹣2＞﹣3
则这天气温最低的城市是张家界。
故答案为：B
【点睛】本题考查正负数的大小比较，明确其比较大小的方法是解题的关键。
2．B
【分析】在数轴上，首先确定原点0的位置和单位长度，且从左到右的顺序就是数从小到大的顺序，所有的负数都在0的左边，越往左数越小，正数都在0的右边，越往右数越大。点P表示的数所在的位置是在﹣2和﹣1之间，说明这个数大于﹣2小于﹣1。据此判断即可。
【详解】A．﹣2.5＜﹣2，不符合题意；
B．﹣2＜﹣1.5＜﹣1，符合题意；
C．0.5＞﹣1，不符合题意；
D．1.5＞﹣1，不符合题意；
故答案为：B
【点睛】此题主要考查了正负数在数轴上的表示以及正负数的大小比较。
3．D
【分析】
由题意可知，需缴税部分是（3000－1200）元，按20%的税率缴税，根据求一个数的百分之几是多少，用乘法计算，即可求出要缴税的税额。
【详解】（3000－1200）×20%
＝1800×0.2
＝360（元）
这笔劳务费一共要缴税360元。
故答案为：D
4．A
【分析】根据利息公式：利息＝本金×利率×时间，代入数据，求出到期后的利息，再加上本金，即可求出到期后一共取回的钱数。
【详解】60000×2.25%×3＋60000
＝1350×3＋60000
＝4050＋6000
＝64050（元）
今年玉米取得了大丰收，小红家把卖玉米所得的60000元钱存入银行3年，年利率是2.25%，到期后小红家一共可取64050元。
故答案为：A
5．A
【分析】根据公式：本金×利率×存期；先算出爸爸2万元买3年国债到期的利息，20000×3.42%×3＝2052元，加上本金，20000＋2052＝22052元；爸爸买理财产品收益：第一年为：20000×3.2%＝640元，本金＋利息为： 640＋20000＝20640元；第二年为：20640×3.2%＝660.48元，本金＋利息为：20640＋660.48＝21300.48元；第三年为：21300.48×3.2%≈681.62元，本金＋利息为：21300.48＋681.62＝21982.1元；比较收益的大小，即可解答问题。
【详解】3年期国债：20000×3.42%×3
＝684×3
＝2052（元）
先买一年期，把本金和利息取出来合在一起，再存入一年：
第一年为：20000×3.2%＝640（元）
本金＋利息为： 640＋20000＝20640（元）
第二年为：20640×3.2%＝660.48（元）
本金＋利息为：20640＋660.48＝21300.48（元）
第三年为：21300.48×3.2%≈681.62（元）
本金＋利息为：21300.48＋681.62＝21982.1（元）
21982.1－20000＝1982.1（元）
2052＞1982.1
买3年国债收益更大。
故答案为：A
【点睛】本题考查了利息相关问题，熟练掌握它的公式并灵活运用。
6．C
【分析】把一根圆柱形钢材截成三段后，增加的表面积是4个底面的面积之和，先计算出一个底面的面积，再根据圆柱的体积＝底面积×高，代入数值计算，据此解答。
【详解】1.2m＝12dm
3.6÷4×12
＝0.9×12
＝10.8（dm3）
因此这根圆柱形钢材原来的体积是10.8dm3。
故答案为：C
7．A
【分析】图中AB为圆柱的高，将圆柱的侧面沿高展开，得到长方形，长为圆柱底面周长，宽为圆柱的高，当底面周长等于高时，侧面沿高展开得到的图形为正方形；将圆的侧面沿高展开得到的图形只能为长方形或正方形，不可能是梯形或圆，据此解答。
【详解】根据分析可知，将圆柱体的侧面沿AB剪开再展开，所得到的侧面展开图可能是或。
故答案为：A
【点睛】熟练掌握圆柱的侧面展开图的特征是解答本题的感觉。
8．B
【分析】根据圆柱的侧面积＝底面周长×高，底面直径不变是10cm，高增加2cm，代入相应的数值计算，即可得出结论。
【详解】原侧面积：3.14×10×高；
高增加2cm后的侧面积：3.14×10×（高＋2）；
3.14×10×（高＋2）－3.14×10×高
＝31.4×高＋31.4×2－31.4×高
＝31.4×2
＝62.8（cm2）
因此高增加2cm，则侧面积增加62.8cm2。
故答案为：B
【点睛】解答本题的关键是注意底面直径不变，高增加2cm，根据圆柱侧面积的计算公式来求解。
9．﹢5
【分析】用正负数表示意义相反的两种量：高于平均身高记作正，低于平均身高的记作负，据此解答。
【详解】如果用﹣2厘米表示比平均身高底2厘米，那么比平均身高高5厘米可记作﹢5厘米。
10．295
【分析】净含量300克±5克，表示这种食品标准的质量是300克，实际每袋最多不多于（300＋5）克，最少不少于（300－5）克。
【详解】300－5＝295（克）
某种品牌洗衣粉的包装袋上写着净含量300克±5克，这表示这袋洗衣粉的标准质量是300克，实际质量最少不少于295克。
11．﹣0.1%
【分析】此题主要用正负数来表示具有意义相反的两种量：增长的百分率记为正，则下降的百分率记为负，直接得出结论即可。
【详解】如果把“增长2.2%”表示为﹢2.2%，那么“下降0.1%”表示为﹣0.1%。
【点睛】此题主要考查正负数的意义，正数与负数表示意义相反的两种量，看清规定哪一个为正，则和它意义相反的就为负。
12．90
【分析】将消费金额看作单位“1”，几折就是百分之几十，打八折可以少花（1－80%），消费金额×少花的对应百分率＝少花的钱数，据此列式计算。
【详解】450×（1－80%）
＝450×0.2
＝90（元）
她们可以少花90元。
13． 25% 120
【分析】增长二成五，即增长25%。今年接待游客数=去年接待游客数（125%），根据百分数运算法则计算得出答案。
【详解】比去年增长二成五，表示今年旅游总人数比去年增加25%。今年接待游客人数为：
（万人）
14． 19.5 58.5
【分析】等底等高的圆柱和圆锥，圆柱体积是圆锥体积的3倍，根据和倍问题解题方法，体积和÷（倍数＋1）＝圆锥体积，体积和－圆锥体积＝圆柱体积，据此列式计算。
【详解】78÷（3＋1）
＝78÷4
＝19.5（立方分米）
78－19.5＝58.5（立方分米）
圆锥的体积是19.5立方分米，圆柱的体积58.5立方分米。
15． 24 8
【分析】等底等高的圆柱的体积是圆锥体积的3倍，所以等底等高的圆柱与圆锥的体积差相当于圆锥体积的（3－1）倍，即用圆柱比圆锥体积大的部分除以（3－1）即可求出圆锥体积；
根据圆锥的体积公式：V＝Sh，那么h＝V÷÷S，代入公式求出圆锥的高即可。
【详解】由分析可得：
等底等高的圆柱的体积是圆锥体积的3倍，
48÷（3－1）
＝48÷2
＝24（cm3）
24÷÷9
＝24×3÷9
＝72÷9
＝8（cm）
综上所述：一个圆柱和一个圆锥等底等高，已知圆柱的体积比圆锥大48cm3，那么圆锥的体积是24cm3。如果圆锥的底面积是9cm2，那么圆锥的高是8cm。
16． 8 4 401.92
【分析】观察图形可知，长方形的长等于圆的周长，长方形的高等于圆柱的高，圆柱的高是8厘米；根据圆的周长公式：周长＝π×半径×2，半径＝周长÷π÷2，代入数据，求出圆柱底面半径；再根据圆柱的体积公式：体积＝底面积×高，代入数据，即可解答。
【详解】圆柱的高是8厘米；
半径：25.12÷3.14÷2
＝8÷2
＝4（厘米）
体积：3.14×42×8
＝3.14×16×8
＝50.24×8
＝401.92（立方厘米）
如图，它是一个圆柱的表面展开图，那么这个圆柱的高是8厘米，底面半径是4厘米，体积是401.92立方厘米。

【点睛】熟练掌握圆柱的特征、圆的周长公式、圆柱的体积公式是解答本题的关键。
17．×
【分析】﹣5摄氏度是零下5摄氏度，8摄氏度是零上8摄氏度。将5摄氏度加上8摄氏度，求出这天的最大温差。
【详解】5＋8＝13（摄氏度）
所以，这天的最大温差是13摄氏度。
故答案为：×
18．×
【分析】设这件商品的原价是1，先把这件商品的原价看作单位“1”，打折后的价格是原价的80%，根据求一个数的百分之几是多少，用乘法求出打折后的价格；
再把打折后的价格看作单位“1”，提价后的价格是打折后价格的（1＋20%）；单位“1”已知，用乘法求出现价，再与原价相比较，得出结论。
【详解】设这件商品的原价是1。
1×80%×（1＋20%）
＝1×0.8×1.2
＝0.96
0.96＜1
现价比原价低。
原题说法错误。
故答案为：×
【点睛】本题考查百分数的实际应用，区分两个单位“1”的不同，单位“1”已知，根据百分数乘法的意义解答。
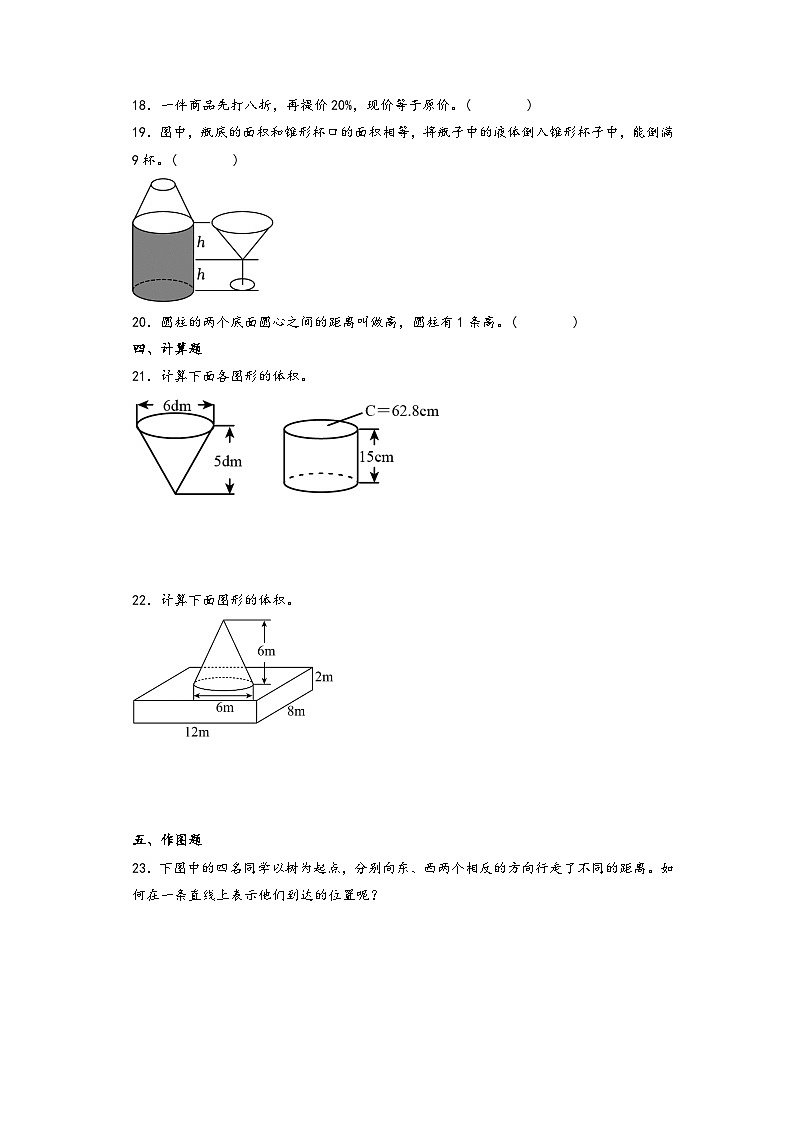
19．×
【分析】由图可知，圆柱的底面积和圆锥的底面积相等，把瓶子中的液体看作一个圆柱，圆柱的一半与圆锥等底等高，当圆柱和圆锥等底等高时，圆柱的体积是圆锥体积的3倍，液体的一半倒入锥形杯子中可以倒3杯，那么全部液体可以倒6杯，据此解答。
【详解】分析可知，把瓶内液体的体积看作与锥形杯子等底等高的两部分，一部分倒入锥形杯子中可以倒3杯。
3×2＝6（杯）
所以，能倒满6杯。
故答案为：×
【点睛】掌握等底等高的圆柱和圆锥之间的体积关系是解答题目的关键。
20．×
【详解】如图：
圆柱的两个底面之间的距离叫做高，圆柱有无数条高。
原题说法错误。
故答案为：×
21．47.1dm3；4710cm3
【分析】（1）已知圆锥的底面直径和高，根据圆锥的体积公式V＝πr2h，代入数据计算即可求解。
（2）已知圆柱的底面周长，根据圆的周长公式C＝2πr可知，r＝C÷π÷2，由此求出圆柱的底面半径；再根据圆柱的体积公式V＝πr2h，代入数据计算即可求解。
【详解】（1）×3.14×（6÷2）2×5
＝×3.14×9×5
＝47.1（dm3）
圆锥的体积是47.1dm3。
（2）圆柱的底面半径：
62.8÷3.14÷2
＝20÷2
＝10（cm）
圆柱的体积：
3.14×102×15
＝3.14×100×15
＝4710（cm3）
圆柱的体积是4710cm3。
22．248.52m3
【分析】观察图形可知，该立体图形的体积等于长方体的体积加上圆锥的体积，根据长方体的体积公式：V＝abh，圆锥的体积公式：V＝πr2h，据此代入数值进行计算即可。
【详解】圆锥的体积：
×3.14×（6÷2）2×6
＝×3.14×32×6
＝×3.14×9×6
＝×6×3.14×9
＝2×3.14×9
＝6.28×9
＝56.52（m3）
长方体的体积：
12×8×2
＝96×2
＝192（m3）
组合图形的体积：
56.52＋192＝248.52（m3）
23．见详解
【分析】向东和向西意义正好相反，可以用正负数来表示他们行走的方向和到树的距离；可以用0表示树的位置，用﹢2表示树东边2米的位置，用﹣2表示树西边2米的位置，用﹢4表示树东边4米的位置，用﹣4表示树西边4米的位置，这样就可以在一条直线上表示他们到达的位置了。
【详解】如图所示：
24．（1）﹢4；0
（2）87分
【分析】（1）大于平均分的分数，就用得分减去平均分，再加上正号，小于平均分的分数，就用平均分减去得分，再加上负号即可；
（2）应用上面的方法，计算出三名同学的得分，再除以3即可。
【详解】（1）89－85＝4，记作﹢4分，85－85＝0，记作0分；
（2）85＋8＝93（分）
85－5＝80（分）
85＋3＝88（分）
＝261÷3
＝87（分）
答：这三名同学的平均分是87分。
【点睛】此题首先以平均分为标准，规定超出标准的为正，低于标准的为负，由此用正负数解答问题。
25．（1）5名；（2）62.5%
【分析】（1）观察统计表，统计出其中的0和正数的个数，有多少个，那么第一小组就有多少名男生达到标准；
（2）用达标人数5人除以第一组的总人数8人，求出达标学生数占全组人数的百分之几。
【详解】（1）答：第一组男生成绩达标的有：1、0、0、0、2，共5个，所以第一小组有5名男生达到标准。
（2）5÷8＝62.5%
答：达标学生数占全组人数的62.5%。
【点睛】本题考查了正负数的应用，如果正数表示达到标准，那么负数表示没有达标。
26．丙书店
【分析】根据题意，分别求出三家书店需要的钱数，找出用钱最少的一家。
【详解】甲书店：12×12×80%
＝144×80%
＝115.2（元）
乙书店：12÷（5＋1）×5
＝12÷6×5
＝2×5
＝10（本）
10×12＝120（元）
丙书店：12×12＝144（元）
144－15×2
＝144－30
＝114（元）
114＜115.2＜120
答：到丙书店购买最合算。
27．1.96万吨
【分析】前年比去年少三成，也就是前年的秋粮食产量比去年少30%，去年秋粮食产量是单位“1”，去年秋粮食产量为2.8万吨，求比一个数少百分之几的数是多少的解题方法：单位“1”的量×（1－百分之几）。据此求前年秋粮食产量列式为：2.8×（1－30%）。
【详解】2.8×（1－30%）
＝2.8×70%
＝1.96（万吨）
答：前年秋粮食产量是1.96万吨。
28．626762.5元
【分析】单价×数量＝总价，据此用6500乘100可以求出这套房子的房款。一次性付清了房款，享受了九五折优惠，根据“求一个数的百分之几是多少，用乘法计算”，用房款乘95%即可求出房子的成交价。再用成交价乘1.5%可以求出契税的钱。最后用成交价加上缴纳的契税，即可求出园园家购房实际花了多少钱。
【详解】100×6500×95%
＝650000×0.95
＝617500（元）
617500＋617500×1.5%
＝617500＋9262.5
＝626762.5（元）
答：园园家购房实际花了626762.5元钱。
29．114.35元
【分析】根据利息＝本金×利率×存期，分别计算两种理财方式的到期利息，最后用减法计算两种理财方式的利息差即可。
【详解】1万元＝10000元
3年期国债的利息：10000×3.35%×3
＝335×3
＝1005（元）
买银行一年期理财产品：
第一年的利息：10000×3.6%＝360（元）
第二年的利息：（10000＋360）×3.6%
＝10360×3.6%
＝372.96（元）
第三年的利息：
（10000＋360＋372.96）×3.6%
＝（10360＋372.96）×3.6%
＝10732.96×3.6%
≈386.39（元）
三年的利息：
360＋372.96＋386.39
＝732.96＋386.39
＝1119.35（元）
1119.35－1005＝114.35（元）
答：两种理财方式的收益相差114.35元。
30．2499立方厘米
【分析】已知圆柱的底面直径和高，只需要求出圆锥高即可。根据正放时水面离容器顶部11厘米，假设圆锥部分的高为厘米，如下图，则正放时空气部分的体积相当于高为的圆锥的体积加上高为（11－）的圆柱部分的体积。而圆柱和圆锥是等底的，根据等底的圆柱和圆锥的体积关系，高为的圆锥体积也可以看成是高为的圆柱的体积，这样正放时空气部分的体积相当于高为的圆柱体积。因为无论正放、倒放，空气体积是不变的，所以这一部分空气体积，也等于倒放时高为5厘米的圆柱的体积。因为圆柱的底面始终一样，所以两部分圆柱的高一定是相等的，即，解方程即可求得的值。再根据圆柱、圆锥的体积公式即可求得这个容器的容积。
【详解】解：设圆锥的高为厘米，


体积：
（立方厘米）
答：这个容器的容积是2499立方厘米。
31．471朵
【分析】由题意可知，花柱的侧面和上面都插满鲜花，则插鲜花的面积就是圆柱的侧面积加上圆柱的底面积，根据圆柱的侧面积公式：S＝πdh，圆的面积公式：S＝πr2，据此求出插鲜花的面积；再用插鲜花的面积乘每平方米可装饰花的朵数即可求解。
【详解】3.14×0.52＋3.14×（0.5×2）×3.5
＝3.14×0.25＋3.14×1×3.5
＝0.785＋10.99
＝11.775（平方米）
11.775×40＝471（朵）
答：这根花柱一共需要471朵花。
32．7厘米
【分析】若将这个容器倒立，沙子的总体积不变，根据圆柱的体积公式：V＝πr2h和圆锥的体积公式：V＝πr2h，用3.14×62×2＋3.14×62×15×即可求出沙子的体积，然后用沙子的体积÷（3.14×62）即可求出倒立后沙子的高度。
【详解】3.14×62×2＋3.14×62×15×
＝3.14×36×2＋3.14×36×5
＝113.04×2＋113.04×5
＝226.08＋565.2
＝791.28（立方厘米）
791.28÷（3.14×62）
＝791.28÷（3.14×36）
＝791.28÷113.04
＝7（厘米）
答：细沙的高度是7厘米。